Au-delà de la relativité générale

A - La géométrisation de la physique

Même si la géométrie avait toujours influencé les théories sur la structure du Monde (cf. Platon et les polyèdres) et que la géométrie abstraite avait commencé à s'imposer en physique avant l'arrivée de la théorie de la relativité d'EinsteinEinstein¹, celle-ci marqua néanmoins le début d'une nouvelle ère. En effet, avec elle, pour la première fois dans l'histoire de la science moderne, la géométrie n'était pas utilisée uniquement comme un outil commode, et un phénomène physique bien concret, à savoir la gravitation, trouvait une explication purement géométrique. Le succès de cette nouvelle "géométrisation" de la physique fut tel que, dès 1919, de très nombreuses personnes essayèrent d'élargir le cadre géométrique proposé par la relativité générale pour décrire plus de phénomènes physiques, Einstein consacrant lui-même de longues années à la recherche d'une théorie unifiée dans laquelle la gravitation et l'électromagnétisme seraient "géométrisés". Cependant, alors qu'à la naissance de la relativité générale on pouvait encore presque croire que la gravitation et l'électromagnétisme étaient les seules interactions à prendre en compte, la découverte de la désintégration beta, puis celle des constituants des noyaux atomiques, rendirent un peu caduccaduc le principe consistant à ne considérer que celles-ci. De plus, l'avénement de la physique quantique bouleversa complètement le cadre conceptuel, introduisant un formalisme mathématique tout aussi nouveau que la géométrie différentielle. Du fait de cette richesse historique, la suite de ce chapitre sera inévitablement inexhaustive, seuls étant cités quelques personnages et idées parmi ceux qui semblent aujourd'hui encore les plus importants.

Parmi ceux-ci, le mathématicienmathématicien polonais Theodor Kaluza est très connu pour avoir démontré que la théorie de Maxwell de l'électromagnétisme et la relativité générale pouvaient facilement être retrouvées à partir d'une théorie relativiste géométrique à 5 dimensions (quatre d'espace et une de temps). Plus précisément, il découvrit² que si l'on part d'une métrique sur un espace-tempsespace-temps de dimension 5 et qu'on lui impose d'obéir à la généralisation naturelle des équationséquations d'Einstein, on trouve que cette métrique se décompose naturellement en un quadrivecteur vérifiant des équations très similaires à celles de Maxwell, plus un tenseurtenseur métrique quadridimensionnel qui vérifie des équations très semblables à celles d'Einstein en quatre dimensions. Toutefois, afin de retrouver exactement les équations de Maxwelléquations de Maxwell et de rendre compte de l'observation d'un espace-temps seulement quadridimensionnel, Kaluza dut supposer que les variables physiques étaient indépendantes de la cinquième coordonnée. Ce traitement ad hoc (proposé en 1921) fut amélioré quelques années plus tard (en 1926) par le physicienphysicien suédois Oskar Klein, dont l'apport très original fut de proposer que cette cinquième dimension soit "repliée sur elle-même", soit en termes modernes "compactifiée". Cette hypothèse expliquait en effet "physiquement" pourquoi la cinquième dimension était inobservable, si l'on supposait de plus que la taille de l'enroulement était très petit (de l'ordre de la longueur de Plancklongueur de Planck, 10^-35m), ce qui permettait également de justifier le fait que l'interaction électromagnétique entre deux électronsélectrons est bien plus intense que leur attraction gravitationnelle. Avec cette idée d'une cinquième dimension compactifiée, un déplacement le long de la cinquième dimension est physiquement perçu dans notre monde quadridimensionnel comme un "changement de phase" de l'onde électromagnétiqueonde électromagnétique et/ou quantique, ce qui a pour autre conséquence plaisante d'expliquer la quantificationquantification de la charge électrique.

Cependant, la théorie de Kaluza-Klein présentait divers problèmes qui firent qu'elle resta dans l'oubli pendant quelques décennies. En particulier, le découpage 4+1 de la métrique pentadimensionnelle impliquait également l'existence d'un champ scalaire ("le dilaton"), qui ne correspondait à rien de connu à l'époque. De plus, les années 1920-1930 furent celles durant lesquelles surgit la physique quantique, et assez rapidement on réussit à quantifier l'électromagnétisme (cf. l'électrodynamique quantiqueélectrodynamique quantique brièvement décrite dans le dossier sur la relativité restreinterelativité restreinte), alors qu'une théorie quantique de la gravitation reste encore aujourd'hui une sorte de Graal, ce qui ne fit qu'accentuer le désintérêt pour une théorie non-quantique unifiée. Néanmoins, ces deux caractéristiques font aussi partie des raisons pour lesquelles le principe de dimensions supplémentaires compactifiées fut remis au goût du jour pour la théorie des supercordesthéorie des supercordes dans les années 1980. Avant d'en arriver à celle-ci et aux essais plus modernes, une autre approche souvent adoptée pour généraliser la théorie d'Einstein reste toutefois à mentionner. Il s'agit de l'approche consistant non pas à modifier le nombre de dimension de l'espace-temps, mais à changer la nature de la modélisationmodélisation géométrique de ce dernier. Ainsi, partant d'une "variété" de dimension quelconque, on peut introduire des "structure de mesure" plus générales que le tenseur métrique utilisé en relativité et géométrie riemannienne. Par exemple, il est assez simple de constater que si l'on ne suppose pas, comme on le fait en géométrie riemannienne, que celui-ci est symétrique, cela ne modifie en rien les notions de mesure de distances ou de normes, mais les mesures d'angles sont affectées. Ce type de généralisation de la relativité fut essayé (en vain) dès 1921 par le physicien allemand Ernst Reichenbächer, et plus tard (1948) par le physicien autrichien Erwin SchrödingerErwin Schrödinger, père de l'équation fondamentale de la physique quantique. Finalement, une autre approche consiste à rester en quatre dimensions, et à faire jouer le rôle crucial non pas à la métrique, mais à un autre objet mathématique nommé "connexion", qui sert à comparer les valeurs de diverses grandeurs mathématiques en des points différents d'une variété. Or, si cette notion de connexion intervient beaucoup en relativité générale, il s'avère que l'on peut également la formuler de façon plus générale dans le cadre des géométries affine ou métrique-affine, ce qui est une autre procédure géométrique pour enrichir le cadre de la théorie. Cette méthode fut utilisée par Cartan (qui contribua énormément au développement de la géométrie différentielle), mais également par Einstein, et elle redevint très à la mode récemment grâce au physicien indien A. Ashtekar, lequel introduisit une reformulation de la relativité générale reposant sur la notion de connexion qui est à la base de la "loop quantum gravity" ("gravitation quantique à bouclesgravitation quantique à boucles"), l'une des théories modernes les plus prometteuses vers la quantification de l'interaction gravitationnelle. Un autre "ingrédient mathématique" fondamental utilisé par Ashtekar, et par d'autres que lui auparavant, est la notion de "nombres complexes", ces nombres généralisant les nombres réels de manière telle que la donnée d'un nombre complexe est équivalente à celle d'un couple de réels. On devine aisément ainsi qu'il s'agit d'une autre méthode pour multiplier le nombre de variables dynamiques possibles, tout en gardant un cadre géométrique de dimension 4 (voir aussi plus loin le bref commentaire sur la théorie des "twistors" développée par Penrose). Toutefois, avant d'en venir aux théories les plus modernes (théorie des supercordes et loop quantum gravity), il est nécessaire de décrire également un peu certaines généralisations de la théorie d'Einstein introduites dans les années 1940-1950, et qui reposent sur des hypothèses physiques plutôt que géométriques, la théorie des cordesthéorie des cordes étant d'ailleurs une sorte de mélange de ces deux principes.

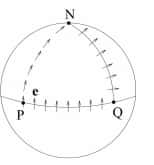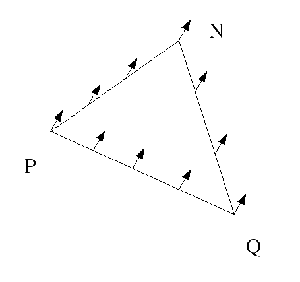
Illustration de la notion de "transport parallèle", qui fait intervenir celle de "connexion", afin de comparer, par exemple, deux vecteurs définis chacun en un point différent d'un espace courbe. Dans l'exemple représenté au-dessus (le plan euclidien), le vecteur est initialement situé en Q. On le fait glisser parallèlement à lui-même le long de la courbe QP, puis le long de la courbe PN, et finalement le long de NQ pour le faire revenir à son point de départpoint de départ. La platitude du plan implique que le vecteur final est identique au vecteur initial. En revanche, dans le cas de la sphère (en dessous), la courbure ressort dans le fait que le vecteur obtenu à la fin de cette procédure est différent du vecteur initial.

B - Le principe d'équivalence, le principe de Mach et les théories tenseur-scalaire

Dans les années qui suivirent la formulation de la relativité générale, il y eut également l'apparition de beaucoup de théories alternatives (non-décrites ici), qui cherchaient à se raccrocher à un espace-temps minkowskien et non courbe. Cependant, certaines autres acceptaient l'idée d'un espace-temps courbe, mais pas celle d'une gravitation qui soit entièrement géométrique. Par exemple, le physicien allemand P. Jordan proposa, à la fin des années 1940, que l'interaction gravitationnelle soit également véhiculée par un champ scalaire physique, et pas uniquement par le tenseur métrique, raison pour laquelle on parle de "théorie tenseur-scalaire". Cette idée fut clarifiée en 1956 par M. Fierz, qui semble avoir été le premier à réaliser que le champ scalaire introduit par Jordan, de même que le "dilaton" résultant de la théorie de Kaluza-Klein, impliquaient la violation possible du principe d'équivalence. En effet, ce champ n'interagit pas nécessairement de la même façon avec toutes les particules, rendant certaines "plus sensibles" à la gravitation que d'autres. Afin de pouvoir séparer les théories tenseur-scalaire qui sont facilement en accord avec les tests précis du principe d'équivalence de celles qui ne le sont pas, Fierz introduisit de manière ad hoc la catégorie des "théories métriques" de la gravitation. Ce sont celles dans lesquelles le principe d'équivalence est vérifié et la gravitation est en partie décrite par un tenseur métrique qui permet de mesurer l'espace-temps. Dans ce cadre, les physiciens américains Carl Brans et Robert Dicke proposèrent en 1961 une théorie (très semblable à celle proposée par Fierz à partir de la théorie de Jordan), qui est également soumise à la contrainte de compatibilitécompatibilité avec le principe de Mach.

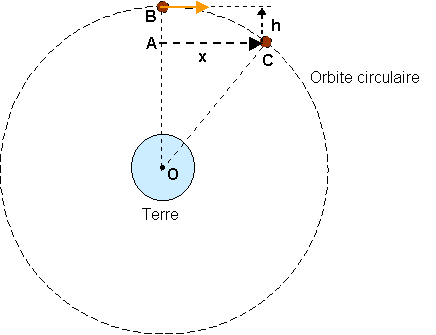
Comme cela a déjà été signalé, cette affirmation peut être interprétée de nombreuses façons, étant données les diverses manières de formuler le principe de Mach. La question que Brans et Dicke se posèrent au sujet de ce principe est en fait de savoir si des forces d'inertieinertie (telles l'effet Lense-Thirringeffet Lense-Thirring) pouvaient apparaître pour un objet en rotation dans un UniversUnivers vide de matièrematière. Mais Brans et Dicke reposèrent également leur théorie sur une constatation numériquenumérique : si l'on calcule le nombre

R_u c² / M_u ,

où R_u est le rayon de l'Univers visible (environ 10 milliards d'années-lumièreannées-lumière), c la vitesse de la lumièrevitesse de la lumière et M_u, la massemasse de l'Univers visible (estimée à partir de sa densité et de son volumevolume), on trouve un facteur qui n'est "pas très" éloigné de la constante de NewtonNewton G (il y a "juste" un facteur 100 entre les deux). Ainsi, dans la lignée de Mach, Dicke se demanda si G n'était pas déterminée par le contenu de l'Univers, ce qui impliquerait (si cette hypothèse était vérifiée) que la constante de la gravitationconstante de la gravitation changerait avec le temps.

A partir de ces réflexions, Brans et Dicke développèrent une théorie tenseur-scalaire alternative à la relativité générale dans laquelle la force de l'interaction gravitationnelle dépend de ce champ scalaire nouvellement introduit. Pouvant donner des prédictions très similaires à celles de la relativité générale, cette théorie fut très en vogue dans les années 1960-1970, mais la précision des tests augmentant, il fut assez rapidement démontré que le modèle le plus simple de la théorie ne pouvait pas concurrencer la théorie d'Einstein. Toutefois, parmi les prédictions des théories de supercordes, nées de la prise en compte de la physique quantique, il y a l'existence de champs scalaires qui pourraient donner des déviations du même type vis-à-vis de la relativité générale, avec cependant des effets locaux bien plus faibles, et qui sont donc toujours compatibles avec les résultats expérimentaux actuels.

C - La gravitation quantique

Le problème de trouver une théorie quantique de la gravitation est l'un des plus difficiles parmi ceux auxquels les physiciens théoriciens ont été confrontés au cours des dernières décennies. Du fait de l'interprétation géométrique de la gravitation, il ne s'agit en effet pas simplement de l'incompatibilité entre deux modélisations d'une interaction, mais également de celle entre deux cadres conceptuels pour la physique et du besoin de rechercher une "géométrie quantique". Ainsi, l'une des notions les plus importantes en physique quantique est celle "d'unitarité", qui décrit grossièrement le fait que la somme des probabilités d'un événement doit être conservée dans le temps, étant toujours égale à 1. Or, la relativité générale explique également que la notion de temps ne peut pas être absolue et que ce qui est pour un observateur le temps peut être pour un autre un mélange subtil entre espace et temps, ce qui complique terriblement la constructionconstruction d'une théorie unitaire qui soit en accord avec les "principes de base" de la relativité. Par ailleurs, un autre élément-clé de la physique quantique est la notion "d'indétermination" (d'Heisenberg) du résultat d'une mesure, ce qui est en opposition avec le déterminisme de la relativité générale. Il faut toutefois noter que ces problèmes apparaissent uniquement lorsque l'on cherche à quantifier le champ de gravitation lui-même et non pas si l'on cherche à décrire l'évolution d'un champ quantique dans un espace-temps courbe fixé. Ces deux théories ne sont donc pas en désaccord complet sur tout, les difficultés étant vraiment liées à la façon dont est modélisée la structure de l'espace-temps.

Néanmoins, si l'on applique naïvement les principes quantiques à la notion d'espace-temps dynamique, il ressort qu'aux petites échelles auxquelles on ne peut pas négliger les fluctuations quantiques, le "tissu d'espace-temps", qui est plutôt lisse et calme aux grandes échelles considérées en relativité générale, doit être une sorte de bouillonnement incessant.

Cliquez pour agrandir. Illustration de la façon dont, selon les idées de géométrie quantique, l'espace-temps doit pouvoir être "visualisé" à différentes échelles. Aux plus grandes échelles, il est lisse (mais possiblement courbe), comme en relativité générale. A partir de l'échelle de Planck (environ 10-33 cm), on s'attend à ce que les fluctuations soient très importantes et absolument pas négligeables.

Un problème théorique de taille, illustré sur la figure précédente, est le fait que des "trous" peuvent apparaître au cours des fluctuations de l'espace-temps, ce que l'on traduit en langage mathématique comme des "changements de topologie". Ces changements de topologie aux petites échelles sont d'ailleurs, d'un point de vue technique, reliés à l'une des difficultés dans la quantification de la gravitation, et qui vient de son comportement vis-à-vis d'une procédure mathématique habituellement employée dans la recherche de la formulation quantique d'interaction : la "renormalisation". On peut en effet montrer que cette procédure, qui consiste grossièrement à réussir à faire des calculs à une échelle donnée même si l'on n'est pas capable de les faire avec une seule formule valable à toutes les échelles, implique dans le cas de la gravitation l'apparition de termes infinis de plus en plus nombreux quand on avance dans le calcul. Pour l'électromagnétisme ou l'interaction électrofaible, certains termes infinis apparaissent, mais on peut les "tuer" à l'aide de termes provenant d'autres échelles. Dans le cas de la gravitation, faire appel aux autres échelles ne fait qu'empirer les choses !

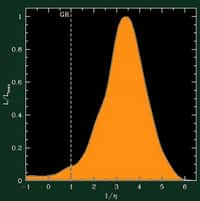
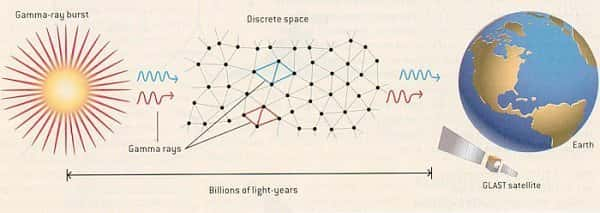
Toutefois, dans la lignée des travaux d'Ashtekar, s'est développée depuis quelques années une nouvelle approche de quantification de la gravitation qui semble très prometteuse. Cette "loop quantum gravity", dont l'un des protagonistes les plus connus est Carlo Rovelli, suppose, en accord avec les principes premiers de la physique quantique, que si l'espace-temps est un objet dynamique "standard", il doit également être "quantifié" et présenter une échelle fondamentale. Cette hypothèse implique l'existence de sortes de "briques insécables" d'espace-temps dont le tissu global serait formé et fait que certains termes infinis sont naturellement éliminés des calculs. Par ailleurs, il découle de cette hypothèse que le principe de constance de la vitesse de la lumière dans le vide devrait être violé aux petites échelles. En effet, ces briques impliquent des inhomogénéités locales de l'espace-temps, inhomogénéités que la lumière devrait percevoir sur de très longs trajets intergalactiques. Ainsi, l'une des méthodes d'ores et déjà employées pour essayer de mettre en évidence de tels effets, et/ou de contraindre les théories qui les prédisent, consiste à chercher d'apparentes violations de la constance de la vitesse de la lumière émise lors de "gamma ray burstsbursts" (explosions très intenses et courtes de rayons gammarayons gamma que l'on pense liées à l'accrétionaccrétion de matière sur des trous noirs supermassifstrous noirs supermassifs), principe qui est illustré sur la figure suivante. Deux lumières de couleurscouleurs différentes vont interagir différemment avec la structure quantique de l'espace-temps, impliquant une dispersion des ondes. Cet effet, inévitable si l'espace-temps est quantifié, n'a toujours pas été observé, cependant, à partir du moment où l'on considère l'espace-temps comme un objet dynamique quantique, il existe peut-être un autre domaine à explorer. De la même façon que la relativité générale avait naturellement débouché sur la cosmologiecosmologie relativiste, une description quantique de l'espace-temps peut en effet a priori impliquer l'émergenceémergence d'une "cosmologie quantique".

Cliquez pour agrandir. Illustration du mécanisme selon lequel la structure quantique de l'espace-temps aux petites échelles pourrait résulter en une variabilité de la vitesse de la lumière. Pour celle-ci, l'effet serait similaire à une interaction avec un "cristal planckien", deux couleurs (longueurs d'ondeslongueurs d'ondes) différentes ne mettant pas le même temps à traverser ce cristal.

D - La cosmologie quantique

Bien avant la naissance de la loop quantum gravity, qui pour le moment s'intéresse avant tout à des problèmes locaux et non à un phénomène aussi global que la cosmologie, l'idée de la cosmologie quantique avait déjà été explorée par diverses personnes. L'approche envisagée alors était cependant différente, reposant sur la quantification "canonique" d'un hamiltonienhamiltonien. La première description de ce genre a été découverte en 1967 par les Américains John Wheeler et Bryce de Witt, qui formulèrent une "équation de Schrödingeréquation de Schrödinger" pour la fonction d'onde de l'Univers, l'équation de "Wheeler-de Witt". Cette équation permet, en théorie, de prédire la probabilité que l'Univers ait une forme donnée (et qu'il la garde), mais en pratique, le cas général est insoluble, l'équation étant bien trop complexe. Divers modèles simplifiés ont donc été proposés, notamment par les Russes A. Lindé et A. Vilenkin, et par les Anglais J. Hartle et S. Hawking.

Les deux modélisations proposées sont très différentes, l'Univers de Lindé et Vilenkin étant une sorte de moussemousse chaotique éternelle ayant un nombre de dimensions indéterminé (un "super-Univers"), dans lequel des fluctuations "locales" formeraient autant d'Univers similaires au nôtre, mais dans lesquels les constantes physiques ne seraient pas nécessairement les mêmes. Par ailleurs, selon les observations récentes, l'Univers aurait commencé sa vie par une phase d'expansion très rapide (que certaines théories expliquent à l'aide de l'existence d'un "dilaton"), phénomène que Lindé et ses collaborateurs ont évidemment pris en compte dans leurs plus récents modèles (voir la figure suivante). Le modèle initial de Hartle-Hawking est quant à lui presque à l'extrême opposée, puisqu'il suppose un Univers unique, fini dans le temps et dans l'espace et sans bord (une "hypersphère"), ce qui éliminerait le problème de la singularité originelle (le Big BangBig Bang). Il faut toutefois noter que cette cosmologie quantique devrait elle aussi prendre en compte la possibilité de fluctuations de la topologie de l'Univers, ce qui implique de faire des calculs similaires à ceux que Feynman introduisit pour l'électrodynamique quantique (les intégrales de chemins), mais dans lesquels chaque "chemin" serait une topologie possible de l'Univers. Autant dire que les difficultés sont immenses et le problème encore imparfaitement résolu, même si le même genre de problèmes techniques survient lorsque, dans une théorie quantiques d'interaction entre "objets", on suppose que ces derniers ne sont pas des "particules ponctuelles" (au sens quantique), mais des objets étendus, telles des (super)cordes.

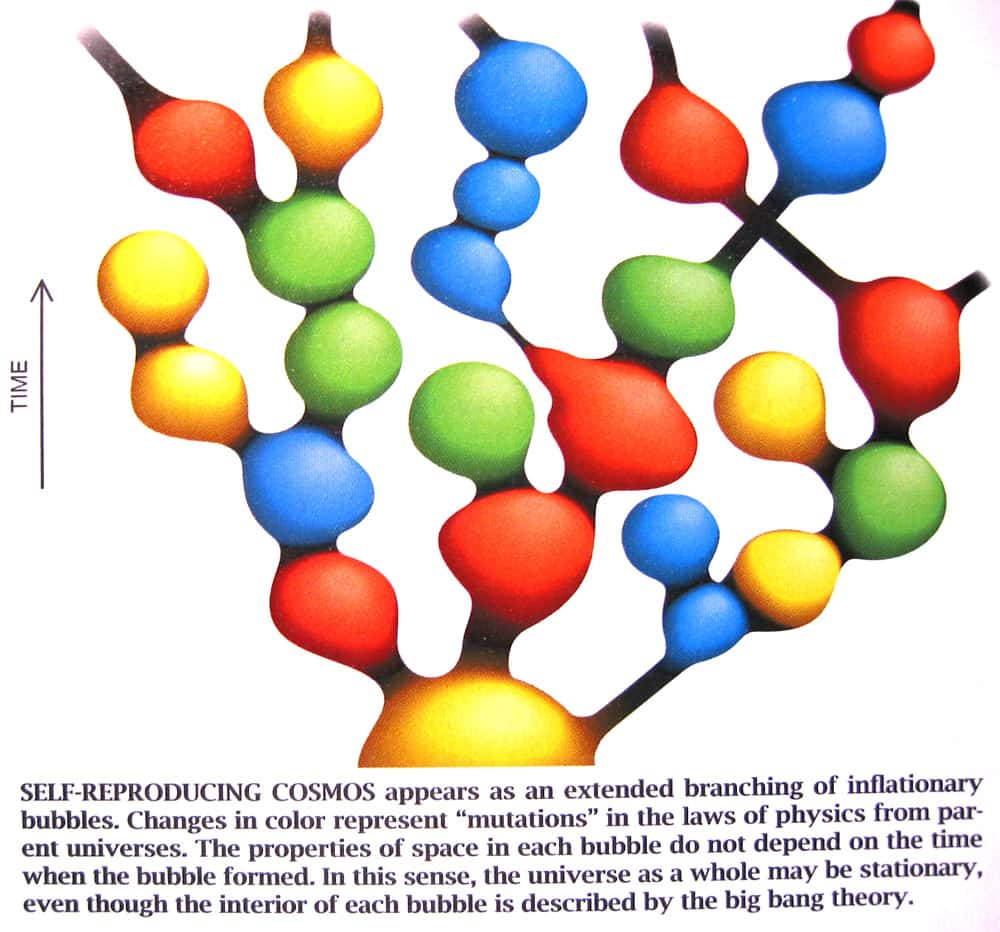
Cliquez pour agrandir. Au-dessus, illustration d'un "modèle" possible d'Univers inflationnaire dans lequel plusieurs univers "parallèles" naîtraient de fluctuations ayant lieu dans un "Univers-père", chaque couleur correspondant à un Univers avec des valeurs différentes des constantes fondamentales. En dessous, comparaison entre l'Univers selon le modèle de Hartle-Hawkingmodèle de Hartle-Hawking et la Terre. Les deux sont dénués de bord et ne présentent pas de singularité aux pôles. Source A. Lindé, S. Hawking.

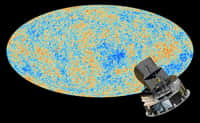
Cependant, avant d'en arriver à une brève description de la théorie des cordes, il reste à mentionner un "élargissement" du cadre de la relativité qui concerne la cosmologie et la topologie, mais pas directement la physique quantique. Il s'agit de la question de la topologie globale de l'Univers. Ainsi, la relativité générale étant une théorie locale, il n'existe aucune prescription pour décrire la forme globale de l'espace-temps. Beaucoup de gens, dont Friedmann dès 1924, se sont donc penchés sur la question de la topologie de l'Univers, certains envisageant de formuler une nouvelle théorie de la gravitation relativiste qui intègre les "conditions aux limites". Ce travail théorique n'a pas réellement abouti, mais une équipe internationale en partie française (J.P Luminet et al.) a récemment proposé qu'un détail, jusqu'alors incompris, dans la cartographie du rayonnement de fond cosmologique puisse s'expliquer par le fait que l'Univers aurait une topologie "avec des trous". Si ce résultat était vérifié par des mesures ultérieures, cela pourrait être un autre important moyen de sonder les aspects les plus énergétiques de la gravitation, puisque la topologie de l'Univers est quelque chose qui devrait normalement être prédit par les théories de cordes ou toute autre théorie quantique qui prétendrait pouvoir traîter de l'Univers primordial. Les théories les plus modernes, issues de celles des cordes, prédisent d'ailleurs un autre type de modèles cosmologiques qui sera brièvement mentionné plus tard : "le modèle branaire".

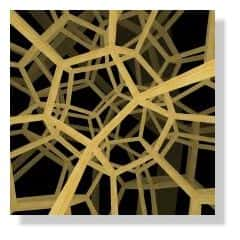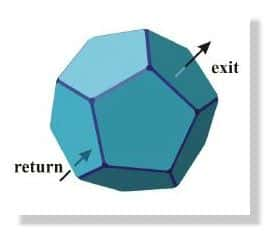
Au-dessus, illustration de l'Univers de Poincaré, utilisé dans le modèle de Luminet et al., qui peut se voir comme une sorte de "ballonballon de foot" formé de 12 pentagones incurvés. Au centre, illustration de la grande différence avec un ballon conventionnel : l'Univers n'est pas "simplement connexeconnexe", et si l'on sort "par une face", on entre à nouveau par la face opposée. En dessous, illustration de ce que perçoit un observateur situé dans un tel Univers : regardant dans une direction donnée, il contemple de très nombreuses répliques de l'Univers physique, un peu comme dans un labyrinthe de glaces. Source J.P. Luminet.

Par ailleurs, dans certaines théories parmi les plus spéculatives, on trouve aussi parfois l'idée que c'est même la topologie de l'espace-temps qui pourrait être complexe, permettant l'existence de "raccourcis au travers de l'Univers", autant dans l'espace que dans le temps, les fameux "trous de ver". Ces objets sont cependant très spéculatifs, même si l'une des explications actuelles possibles du phénomène d'expansion accéléré de l'Univers fait appel à une "énergie noireénergie noire", qui pourrait permettre la survie de ces "tunnels hors de l'espace-temps". Pour conclure ce chapitre sur les extensions possibles de la relativité générale, quelques mots sur la théorie des supercordes semblent donc très appropriés, puisque la plupart des effets qui ont été décrits jusqu'ici peuvent être inclus dans celle-ci ou en sont des conséquences possibles.

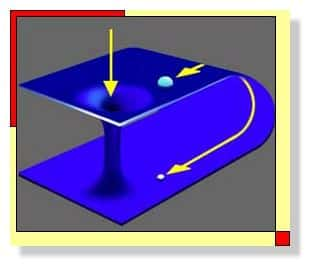Illustration du concept de trou de ver, qui permet de joindre deux points distants de l'espace-temps. Avec de tels objets astrophysiquesastrophysiques, le voyage dans le temps serait éventuellement possible et c'est l'une des raisons pour lesquelles la grande majorité des physiciens pensent qu'il doit exister un mécanisme empêchant leur existence à des dimensions macroscopiques (il a été démontré que seule de la matière "anormale" peut éventuellement empêcher un trou de ver de rapidement se désintégrer). Sur la figure, deux trajets possibles pour rejoindre la Terre depuis l'astreastre du bas sont représentés. Un éventuel engin spatial capable d'entrer dans le trou de ver, et de survivre à sa traversée, pourrait ainsi dans certaines circonstances arriver sur Terre avant la lumière qui aurait emprunté le trajet standard. Source PBS.

E - Les supercordes et la théorie M

L'idée que les "particules ponctuelles" aient des comportement assez semblables à ceux de cordelettes est née en 1968, du physicien italien Veneziano qui tentait de trouver une explication au "confinement des quarksquarks". Les quarks sont les particules constituant ce que l'on nomme les "hadronshadrons", dont le neutronneutron et le protonproton font partie. Or, même si l'on a réussi à mettre en évidence l'existence des quarks à l'intérieur de ceux-ci grâce aux collisionneurs de particules, on n'a jamais observé un quark isolé. Ce qui est désormais expliqué à l'aide de la chromodynamique quantiquechromodynamique quantique était alors un mystère complet, et Veneziano tenta une analogieanalogie avec des cordes pour justifier le fait que lorsque l'on cherche à séparer deux quarks en "tirant" sur chacun d'entre eux, on ne fait que créer deux paires de quarks. La situation est exactement la même si l'on cherche à isoler une extrémité d'un élastique en tirant sur celle-ci : on ne fera rien de mieux que casser l'élastique et obtenir deux "paires d'extrémités" d'élastique, c'est-à-dire deux élastiques.

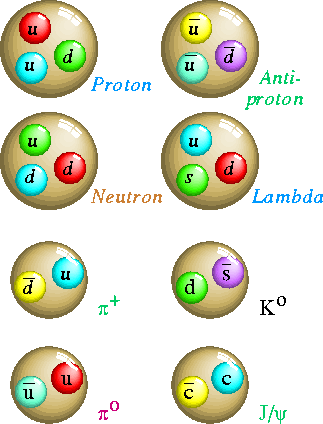Au-dessus, illustration de la composition en quarks des particules les plus courantes (dont le proton et le neutron). En dessous, illustration du phénomène d'apparition de quarks lorsque l'on cherche, par exemple, à séparer deux quarks formant une paire. Le principe physique est que l'énergie fournie lors de la traction finie par se matérialiser sous forme de quarks avant que l'on n'ait réussi à isoler les quarks. Sources G.'t Hooft et  Jefferson Lab.

Veneziano proposa donc que les quarks n'aient pas d'existence réelle, et que les objets fondamentaux derrière ceux-ci soient des cordes. Même si cette idée échoua rapidement dans le cadre de la physique des quarks, des théoriciens commencèrent à se pencher de plus près sur la physique de cordes quantiques, "la théorie des cordes". Parmi les principales différences avec les particules ponctuelles quantiques, figure le fait que puisqu'elle est étendue, même isolée et dans le vide, une corde quantique peut être dans plusieurs niveaux d'énergie différents, chacun correspondant à un mode de vibrationvibration différent. Ainsi, dans une étude qui était avant tout mathématique, on remarqua que dans le "spectrespectre d'oscillation" (= l'ensemble des niveaux d'énergie de la corde), figurait une "particule" sans masse et de spinspin égal à 2. En effet, chaque mode de vibration d'une corde quantique est, pour quelqu'un qui n'aurait pas accès à l'échelle primordiale, perçu comme une particule ponctuelle d'énergie (= masse) différente. Ce qui aurait été vraiment un inconvénient, dans le cadre initial de la physique des quarks, devint donc un grand avantage lorsqu'en 1974, John Schwarz et Joel Scherk réalisèrent que ce modèle apparemment inutile pour la physique nucléaire pouvait se révéler très prometteur si l'on changeait son cadre d'applicationapplication. Une particule de masse nulle et de spin 2 rappelle inévitablement le graviton, particule que doit contenir une théorie quantique de la gravitation, et il devenait ainsi fort possible que les cordes mènent à une théorie quantique de la gravitation, l'idée étant simplement que l'espace-temps soit formé de ces cordes, ce qui, comme dans le cas de la loop quantum gravity, éliminait naturellement certains termes infinis. Néanmoins, plusieurs difficultés apparurent rapidement, puisqu'une autre particule prédite par la théorie était un tachyon, et qu'en plus, on montra que pour la cohérence de l'ensemble, l'espace-temps devait avoir 26 dimensions.

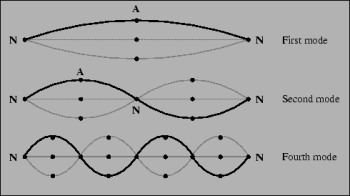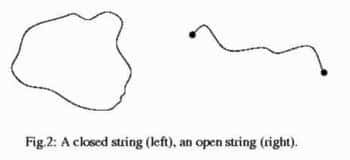
Au-dessus, illustration des cordes les plus simples possibles : ouvertes ou fermées, sans indication d'éventuels degrés de liberté internes. En dessous, représentation des modes d'excitation possibles pour une corde (tout à fait classique) dont les extrémités sont fixées. Plus le nombre de "noeudsnoeuds" est élevé, plus la corde possède d'énergie. De façon analogue, les différents types de (super)cordes sont caractérisés par divers spectres dont les modes d'oscillations (= particules) dépendent des symétries supposées. Plus un mode est élevée, plus la particule correspondante est massive.

Par ailleurs, on avait également appris au début des années 1970 que le rêve d'unification des interactions, qui concernait au début du siècle la gravitation et l'électromagnétisme, n'était peut-être pas si fou que ça puisqu'en 1967, le physicien pakistanais Abdus SalamAbdus Salam et le physicien américain Steven WeinbergSteven Weinberg (se reposant sur des résultats de Sheldon GlashowSheldon Glashow) découvrirent indépendamment l'un de l'autre une même façon de décrire de manière unifiée l'électromagnétisme et l'interaction faibleinteraction faible (qui gouverne certaines désintégrations), par l'intermédiaire d'une seule et unique interaction, l'interaction électrofaible. En outre, un élément-clé de cette théorie était l'introduction de nouveaux champs scalaires (dits de Higgs, du nom du physicien Peter HiggsPeter Higgs) et d'un mécanisme de "brisure spontanée de symétrie", qui expliquaient que le photonphoton soit sans masse alors que les bosonsbosons vecteurs de l'interaction faible sont massifs. Cette théorie et ses prédictions directes furent vérifiées au CERNCERN, le boson de Brout-Englert-Higgs (nommé aussi d'après les physiciens belges Robert Brout et François Englert) ayant notamment été découvert en 2012 au LHC. Mais avant même que tout ne soit vérifié expérimentalement, un formalisme similaire avait été introduit pour essayer de trouver une description unifiée de l'interaction électrofaible avec l'interaction entre quarks. Malheureusement, cela ne semblait pas fonctionner si bien que ça pour diverses raisons techniques qui seront passées sous silence : l'idée d'une "grande unification" des trois interactions précédentes semblait devoir garder le statut de jolie idée mathématique sans rapport avec la physique réelle.

Cependant, certains physiciens, cherchant à étudier qu'elles étaient les symétries les plus générales possibles que l'on puisse incorporer dans des théories de physique des particules remarquèrent que l'on ne pouvait pas "faire n'importe quoi" en mélangeant les symétries spatiales et internes (liées à des nombres quantiquesnombres quantiques), et qu'il existait une sorte de "symétrie maximale" mélangeant ces deux notions de manière subtile, la "supersymétriesupersymétrie". Cette symétrie consiste à associer à chaque particule bosonique un fermionfermion de même masse et réciproquement, ce qui a divers avantages très appréciables, notamment pour éliminer des problèmes d'infinis apparaissant dans les calculs. La supersymétrie étant initialement une symétrie globale de l'espace-temps (qui implique donc le groupe de Poincaré), sa formulation locale devint la "supergravitésupergravité", autre généralisation découverte de la théorie d'Einstein sur laquelle aucun détail supplémentaire ne sera donné ici, bien qu'elle ait récemment été remise au goût du jour grâce à la "théorie Mthéorie M". Néanmoins, il est facile de voir que la supersymétrie n'est pas réalisée dans la nature, puisqu'il n'existe aucun boson de même masse que l'électron, ce qui signifie que si on l'introduit dans une théorie, il faut également expliquer pourquoi elle est brisée. Toutefois, il s'avère que si l'on cherche à appliquer simultanément l'idée de "grande unification" et celle de "supersymétrie" (globale), tous les problèmes ont l'airair de disparaître, au moins en ce qui concerne la théorie.

Or, on peut montrer que pour des raisons techniques, l'ajout d'une supersymétrie dans une théorie est une façon très efficace de "se débarrasser" d'un éventuel tachyon. Ainsi, en 1981, le physicien américain Michael Green, ainsi que son compatriote Schwarz, développèrent une nouvelle théorie de cordes, ou plutôt de "supercordes", reposant sur l'idée de Scherk et Schwarz, mais dans laquelle aucun tachyon ne subsistait, du fait de l'utilisation de supersymétries. Pour toutes les raisons précédemment mentionnées, on en vint donc à voir la théorie des supercordes comme une possible façon d'unifier dans un cadre quantique, toutes les interactions, les supercordes étant à la fois la brique élémentaire pour la matière, les interactions, mais aussi celle pour l'espace-temps. De plus, cette théorie de supercordes prévoyait elle aussi le nombre de dimensions de l'espace-temps dans lequel les cordes "vivaient", et il s'agissait de "seulement" 10 dimensions, et non plus 26. Ce surplus de six dimensions est ce qui motiva la remise à la mode de l'idée de compactification de dimensions, avec toutefois l'apparition de variétés mathématiques bien plus complexes que les simples boucles proposées par Klein : des variétés de Calabi-Yau.

Cliquez pour agrandir. Illustration du principe consistant à compactifier 6 dimensions d'un espace-temps en possédant 10 pour obtenir un espace-temps à 4 dimensions avec, en chaque point de ce dernier, une variété de Calabi-Yau.

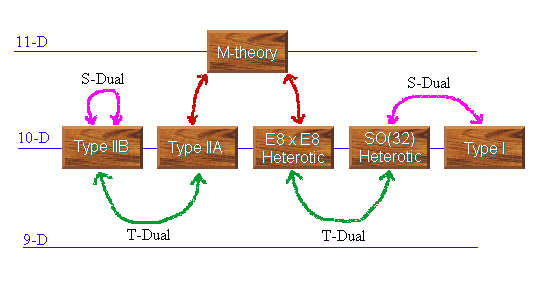
L'utilisation simultanée des notions de supersymétrie, d'unification et de compactification dans la théorie des cordes a donné lieu à ce que l'on nomme la "première révolution des supercordes". Il s'agit de la première, car dans les années 1990, la "seconde révolution" fut déclenchée par E. Witten, P. Townsend et J. Polchinski, qui montrèrent que les 5 théories de supercordes issues de la première révolution pouvaient être perçues comme 5 "limites" différentes d'une théorie plus vaste, la "théorie M" (expression dans laquelle la signification du M n'est pas réellement fixée allant de "magie" à "mystère" en passant par "membrane"), laquelle engloberait également une supergravité en 11 dimensions étudiée par le passé. Cette seconde révolution se fit également avec l'introduction d'objets mathématiques étendues de dimensions variées et sur lesquelles les supercordes seraient "accrochées" : on parle de "branes". Ce qui motiva d'ailleurs toute une nouvelle gamme de modèles cosmologiques (la "cosmologie branaire"), lorsque l'on découvrit des modèles mathématiques d'Univers dans lequels toute la matière vivrait sur une brane à 3 dimensions (qui serait ce que l'on croit être l'Univers), seule la gravitation ayant la possibilité de se promener dans les dimensions supplémentaires. L'originalité de ce modèle, par rapport aux précédents comportant des dimensions supplémentaires, est que puisque la matière est confinée sur la brane tridimensionnelle, les dimensions supplémentaires ne sont pas nécessairement très petites et pourraient avoir une taille de quelques micronsmicrons, voire de presque un millimètre. Ceci impliquerait des déviations par rapport à la loi de Newton aux petites échelles, là où elle n'a pas toujours été très bien testée. Mais cette idée, tout comme les précédentes, reste pour le moment encore un peu floue et incomplète car, malgré les nombreux succès théoriques que beaucoup interprétent comme des signes très favorables, la théorie M, supposée être derrière tout ceci, n'est pas connue. Toutefois, une étape très importante a été franchie avec la compréhension de l'importance de la notion de "dualité" et avec la découverte de telles relations de dualités entre les modèles de supercordes, ce qui signifie que des modèles a priori très différents semblent finalement décrire la même situation physique.

Illustration des relations de dualité existant entre les différentes théories de supercordes et la théorie M. La dualité S relie deux théories qui sont telles que si dans l'une les objets physiques interagissent faiblement entre eux, alors dans la théorie duale il y a une forte interaction entre leurs images. Ce sont donc des échelles d'énergie opposées. La dualité T relie quant à elle des théories d'échelles spatiales opposées : si l'une regarde des petites choses, l'autre décrira des grands objets. Source J.M. Pierre.

Illustration du principe des "branes" sur lesquelles les supercordes seraient "fixées". Source J.M. Pierre.

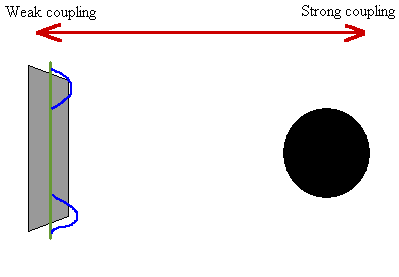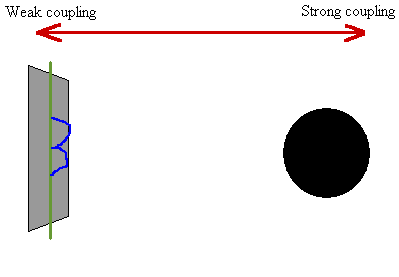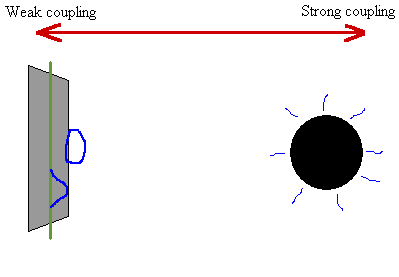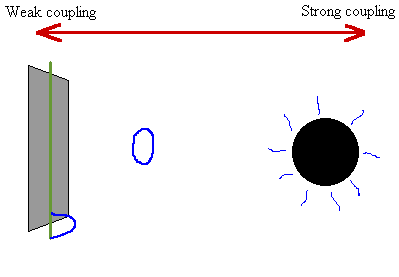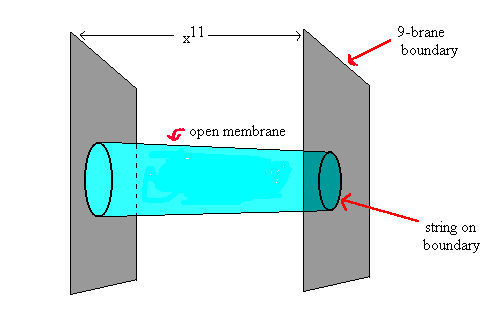
Illustration d'une découverte assez récente illustrant le principe de dualité via les échelles d'énergie et l'importance des trous noirs dans la quête d'une théorie quantique de la gravitation. Il a ainsi été prouvé que la description du rayonnement Hawking d'un certain type de trous noirs plongés dans un certain type d'espace-temps était strictement équivalente à celle de supercordes vivants sur une brane pentadimensionnelle mais à une échelle de faible énergie. Source J.M. Pierre.

Ainsi, cette notion pousse certains à penser que d'autres approches très différentes pour décrire la physique de manière géométrique et unifiée, ne seraient peut-être que d'autres faces de la théorie M. Parmi ces théories et/ou idées actuellement très différentes, figure par exemple la "géométrie non-commutative" de Connes, qui consiste à travailler avec des "coordonnées spatiales" qui ne sont pas des nombres usuels, mais des objets mathématiques tels que le produit A B de deux d'entre eux est différent du produit B A. Une autre approche possiblement très intéressante est la "théorie des twistors" de Penrose, théorie qui semble elle aussi une continuation très naturelle de la relativité générale. L'idée de base de Penrose est également reliée à une sorte de dualité, puisque partant de la constatation qu'un événement (point) de l'espace-temps est caractérisé de manière unique par la donnée du cônecône de lumière associé, il décide de travailler dans un espace géométrique abstrait dont les "points" sont les géodésiques nulles délimitant le cône. De cette façon, apparaît naturellement un espace complexe à partir duquel Penrose espère pouvoir quantifier la gravitation. Bien que l'avis des physiciens théoriciens (qui travaillent sur les théories plus "conventionnelles") sur les chances que Penrose a d'aboutir reste assez partagé, ce dernier a très récemment annoncé avoir trouvé que sa procédure, qui ne requiert l'ajout d'aucune dimension supplémentaire, permet de retrouver les variétés de Calabi-Yau introduite en théorie des supercordes, ces variétés à 6 dimensions pouvant également être considérées comme étant à 3 dimensions complexes.

La conclusion qui devrait ressortir de la lecture de ces tentatives de brèves descriptions des théories les plus modernes est que la situation reste un peu confuse, les théories étant très nombreuses, complexes et surtout encore incomplètes. Ainsi, il est tout à fait possible d'imaginer que parmi celles-ci, plusieurs qui semblent a priori très différentes ne soient effectivement que divers visages d'une même théorie, la théorie M, par exemple. Mais il faut bien comprendre que leur développement est inévitablement un peu "hasardeux", en ce sens où les outils mathématiques appropriés n'ont souvent pas encore été inventés (découverts?) et le sont au fur et à mesure. Toutefois, nous serons probablement un peu plus renseignés dans un futur assez proche, avec la mise en service dans la prochaine décennie du Large Hadron ColliderLarge Hadron Collider, collisionneur de particules actuellement en développement au CERN. Celui-ci devrait atteindre des énergies jusqu'ici inexplorées et dans lesquelles plusieurs des théories mentionnées ici prévoient de nouveaux effets à observer. Parmi les prédictions les plus frappantes pour l'imagination, figure la possibilité de voir des collisions de protons et d'ionsions générer des mini trous noirs de duréesdurées de vie très brèves, identiques à ceux prédits par Hawking. Les trous noirs semblent en effet être fondamentaux pour la théorie M, leur compréhension ayant en retour été améliorée par le recours aux théories dans lesquelles la gravitation est (partiellement) quantifiée. Néanmoins, quelle que soit la théorie qui émergera dans le futur tout en passant avec succès l'épreuve du LHC, il est certain que la conception de l'espace-temps que nous devrons adopter pour l'avenir sera encore plus révolutionnaire que celle apportée par Einstein, certaines idées récentes semblant même soutenir le mythe de la Caverne de Platon selon lequel nous n'observerions que les projections du monde "réel". Il est d'ailleurs fort à parier que, conformément à l'esprit de beaucoup des résultats théoriques les plus récents (présentés ici ou non), il ne s'agira pas seulement de la modification du concept d'espace-temps, mais bien plutôt d'une formulation précise du nouveau concept déjà dans l'air depuis quelques décennies : la matière-espace-temps.

1 on peut penser à l'utilisation de plus en plus courante d'espaces abstraits tels l'espace des phasesespace des phases.

2 selon certaines sources, Kaluza tirerait son idée de la lecture d'articles par Einstein, Lense et Thirring au sujet de l'analogie entre électromagnétisme et gravitation (cf. l'effet Lense-Thirring, sorte de "gravitomagnétisme"). Par ailleurs, il est généralement moins connu que l'introduction d'une cinquième dimension avait en fait déjà été tentée (en vain) auparavant par Nordström dans sa quête d'une théorie relativiste de la gravitation