au sommaire

Le renouveau de la relativité générale : les ondes gravitationnelles
A - La prédiction des ondes gravitationnelles

Peu de gens s'intéressant initialement de très près à ce problème, il fallut attendre le début des années 1960 pour que la question soit presque définitivement éclaircie. Les arguments décisifs pour la communauté vinrent de deux sortes d'études. D'abord, il y eut la réponse, par F. Pirani, à la question "Que verrais-je si une onde gravitationnelle passait dans mon laboratoire ?" Celui-ci démontra ainsi que la "courbure" et l'énergie portées par des ondes gravitationnelles ne pouvaient pas être effacées par un simple changement de coordonnées. Mais les travaux sur les éventuelles sources de rayonnement gravitationnel jouèrent également un rôle important. On peut citer, par exemple, la démonstration, par le mathématicienmathématicien britannique Hermann Bondi, du fait que la "massemasse gravitationnelle" d'un système émettant des ondes gravitationnelles ne pouvait que diminuer. Après le travail de Bondi, il ne restait donc plus qu'à démontrer que cette masse gravitationnelle ne pouvait pas être négative pour qu'aucune critique fondamentale ne puisse plus être adressée à la prédiction de l'existence physique de ces ondes. Cette question, en apparence anodine, ne fut cependant réglée qu'au début des années 1980 par divers physiciensphysiciens dont R. Schoen, S. Yau et E. Witten. Toutefois, indépendamment des questions techniques que soulèvent l'émission et la réceptionréception d'ondes gravitationnelles, on peut essayer de les décrire sommairement et se poser la question des conditions nécessaires (mais peut-être pas suffisantes) pour qu'un système physique soit la source d'ondes gravitationnelles.
Une bonne façon de comprendre la physique des ondes gravitationnelles est de les comparer aux ondes sonoresondes sonores et aux ondes électromagnétiquesondes électromagnétiques prédites par Maxwell. Les ondes sonores sont les ondes associées à la propagation dans un milieu matériel d'un changement de pressionpression. Mathématiquement, on décrit cela par l'oscillation d'un "champ scalaire", la donnée de la valeur de la pression en chaque point de l'espace formant un tel champ. Une simple membrane sphérique, dont la taille change avec le temps, est une source monopolaire d'ondes sonores tout à fait correcte. En revanche, le champ électromagnétiquechamp électromagnétique est un champ vectoriel, ce qui signifie qu'il est décrit par la donnée, en chaque point de l'espace-temps, d'un vecteur. On peut montrer mathématiquement que ceci implique que la particule "véhicule du champ" (le photonphoton) est un bosonboson de spinspin égal à 1, mais aussi que pour émettre une onde électromagnétique, une source doit être associée à une "brisure de la symétrie sphérique au moins dipolaire" (l'absence d'une partie scalaire du champ est liée à la masse nulle du photon). Autrement dit, une antenne qui ne serait qu'un conducteur sphérique, dont la taille varierait cependant avec le temps, n'émettrait aucune onde, comme on peut le constater avec le théorèmethéorème de Gauss qui prédirait, à chaque instant, le même champ électrostatiqueélectrostatique hors de l'antenne. Toutefois, une antenne linéaire dans laquelle une charge positive et une charge négative (qui forment ainsi un dipôle) ont des mouvements oscillatoires opposés (de manière à ce que le barycentrebarycentre de charge ne bouge pas) émet bien du rayonnement électromagnétique.
 | Illustration d'un dipôle électrique formé de deux charges de signes opposés mais de valeurs absolues égales. Pour qu'un tel système émette une onde électromagnétique, il suffit que la distance entre les deux charges change au cours du temps. Source Hyperphysics, C.R. Nave. |
 |
 |
Illustration des concepts d'onde monopolaire (au-dessus) et d'onde dipolaire (en dessous). Source D. Russell. |
Les ondes gravitationnelles sont quant à elles évidemment les vibrationsvibrations du champ gravitationnel, qui est décrit depuis Einstein par le "tenseurtenseur métrique", champ tensoriel d'ordre 2. On peut montrer que le boson vecteur (le probable "graviton") doit avoir un spin égal à 2, et que sa masse nulle (ou de manière équivalente le fait que la vitessevitesse de propagation de la gravitation soit "c") implique que l'émission d'ondes gravitationnelles ne peut se faire qu'avec, au minimum, la variation temporelle de "quadrupôles", ce qui correspond à des déformations encore plus "éloignées" de la forme sphérique que le dipôle. Sur la figure suivante, on peut visualiser une onde scalaire quadrupolaire (à comparer aux ondes monopolaire et dipolaire précédemment présentées) et l'effet attendu d'une onde gravitationnelle sur un cercle de masses ponctuelles. On note la ressemblance entre cette déformation et celle correspondant aux effets de maréesmarées mentionnés plus tôt, ressemblance qui vient du fait que dans les deux cas la courbure est uniquement due à la partie du tenseur de Riemann nommée "tenseur de Weyl".
 |
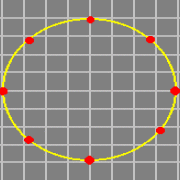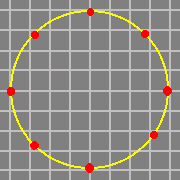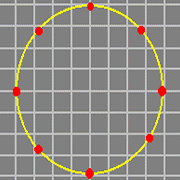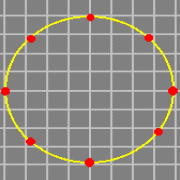 |
Illustration du concept d'onde quadrupolaire (au-dessus) et de l'effet d'une onde gravitationnelle (de polarisation "plus") sur un cercle de masses ponctuelles (en dessous). Sources D. Russell et W. R. Johnston. |
Mais la description de ces caractéristiques des ondes gravitationnelles n'est pas le plus important, car pour pouvoir les détecter, il faut savoir également prédire dans quelles conditions elles peuvent être émises et avec quelles amplitudes et/ou fréquencesfréquences. Une fois encore, Einstein fut l'un des premiers à tenter de répondre à ces questions, même si son modèle initial fut évidemment assez simple. Il regarda ainsi le cas d'une source qui soit une masse accélérée (condition nécessaire à l'émission d'ondes gravitationnelles), mais supposa celle-ci "en mouvement lent", ce qui peut également se dire "la lumièrelumière traverse la source en bien moins de temps que ne le font les constituants de cette dernière" ou encore "la longueur d'ondelongueur d'onde correspondant à la vitesse des constituants est beaucoup plus grande que la taille typique de la source". De plus, il supposa que le champ de gravitation interne était faible, ce qui lui permit de ne regarder que la version "linéarisée" de sa théorie, c'est-à-dire de ne calculer que des petites corrections à la théorie de NewtonNewton.
Même s'il est évidemment hors de question de donner ici plus de détails sur le calcul d'Einstein, on peut néanmoins mentionner qu'il obtint la formule décrivant, en première approximation, l'énergie que perd à chaque seconde un système qui émet des ondes gravitationnelles suite aux "variations temporelles de son quadrupôle de masse" (le quadrupôle de masse étant une sorte de mesure de la déformation par rapport à la sphère). Cette formule donnant la "luminositéluminosité Q" (énergie émise par seconde) peut s'écrire :
Q = (G / c5) s² w6 M² R4,
où l'on a introduit la constante de Newton G, la vitesse de la lumièrevitesse de la lumière c, la fréquence d'évolution (et donc d'émission) w, la taille et la masse typiques du système R et M, ainsi qu'un "facteur d'écart à la symétrie sphérique" s.
Si l'on regarde un objet ordinaire de 1 kilogrammekilogramme, d'une taille de l'ordre de 1 mètre, avec une fréquence de variation de l'ordre de 1 hertzhertz, on constate que le facteur qui régit l'émission est G / c5. Or, si l'on fait le calcul, ce coefficient vaut environ 10-53 en unités du système international... autant dire qu'il est absurde d'espérer produire des ondes gravitationnelles de façon notable en laboratoire. Cependant, la même formule permet de voir quelles sont les conditions nécessaires à l'émission d'ondes gravitationnelles de manière pertinente, si on la réécrit en introduisant
- le rayon de Schwarzschildrayon de Schwarzschild de la source Rs = (2 M c²/ G) ;
- la vitesse caractéristique v associée aux variations du système et définie par v = R w.
En effet, on vérifie aisément qu'à l'aide de ces grandeurs, la formule précédente devient
Q = (c5 / G) s² (v / c)6 (R / Rs)².
Ainsi, on voit que "comme par magie", le facteur de tête a été changé en son inverse (qui est extrêmement grand), et que cette énergie émise sera donc possiblement très importante si les grandeurs caractéristiques de l'objet (son rayon et la vitesse typique de ses variations) sont de l'ordre de son rayon de Schwarzschild et de la vitesse de la lumière. Conclusion : les objets astrophysiquesastrophysiques relativistes et compacts sont de bonnes sources potentielles d'ondes gravitationnelles. Il faut néanmoins éviter d'être trop optimiste, car il est également important d'estimer l'amplitude h que l'on peut espérer pour un signal observé dans le système solairesystème solaire, la formule donnant celle-ci étant :
h = 2. 10-19 ( M / Msol)0.5 ( 1 Mpc / r) ( 1 kHz / f) ( 1 ms / T)0.5 E0.5,
où M est la masse de la source, Msol celle du SoleilSoleil, r la distance entre la source et nous, Mpc désigne un "megaparsec"1, T est la duréedurée de l'émission caractérisée par la fréquence f et E est "l'efficacité du processus", définie par le rapport entre l'énergie totale émise et l'énergie de masse de la source.
On voit ainsi que même si un système astrophysique vérifie les critères pour être une bonne source d'ondes gravitationnelles, les signaux attendus seront de toutes façons très faibles, la valeur h = 10-19 signifiant que l'on doit espérer mesurer des variations de longueur relatives des "détecteurs" de cet ordre de grandeurordre de grandeur. C'est pourquoi, la détection directe d'ondes gravitationnelles reste un véritable défi technologique qui sera brièvement décrit après la présentation de quelques sources astrophysiques potentielles de rayonnement gravitationnel2.
B - Les principales sources possibles d'ondes gravitationnelles
Dans la nature, on connaît plusieurs objets ou phénomènes vérifiant les critères d'émission précédemment décrits. On peut les classer en fonction de la nature du signal que l'on attend d'eux, et on distingue ainsi :
- le fond stochastiquestochastique, composé d'un rayonnement cosmologique primordial et d'une très grande distribution aléatoire de sources régulières ;
- les sources éruptiveséruptives, pour lesquelles on a une émission bien localisée dans l'espace, mais assez limitée dans le temps (par exemple les supernovaesupernovae gravitationnelles ou les binairesbinaires compactes au moment de leur fusionfusion) ;
- les sources périodiques, qui sont localisées spatialement et ont en plus le bon goût de durer et d'être régulières. Parmi celles-ci, on trouve les systèmes binairessystèmes binaires avant effondrementeffondrement et les oscillations d'objets compacts.
1) Fond stochastique
L'une des principales prédictions du modèle du Big BangBig Bang est l'existence d'un rayonnement de fond cosmologique à 3 K, qui a été mis en évidence par Penzias et Wilson. Ce rayonnement électromagnétique résulte grossièrement du découplage entre la matièrematière et les photons, et il constitue l'événement le plus ancien dont peuvent témoigner ces derniers, datant du moment où la matière devint transparente pour eux. Mais la "soupe primordiale" étant composée de nombreux autres ingrédients dont les énergies caractéristiques sont bien plus élevées, plusieurs d'entre eux ont pu se découpler du reste beaucoup plus tôt, ce qui signifie que plusieurs autres types de rayonnement peuvent éventuellement nous permettre de voir plus en arrière dans le passé. Parmi ceux-ci, les gravitons issus de l'ère de PlanckPlanck, et les ondes gravitationnelles associées, sont l'une des plus vieilles reliques que l'on puisse espérer découvrir un jour. Par ailleurs, divers autres objets ou phénomènes cosmologiques sont susceptibles d'avoir généré des ondes gravitationnelles de manière notable. On peut citer les transitions de phasetransitions de phase prédites par les diverses théories d'interaction (du modèle standardmodèle standard ou non), l'évolution ultérieure des défauts topologiques (par exemple les fameuses "cordes cosmiques") auxquels elles peuvent avoir donné naissance, ou encore des événements provenant de scénarios "au-delà de la relativité générale", du type "pré Big Bang" liés aux théories de supercordes ou autres. Ce sont les effets de ce type d'ondes gravitationnelles sur le rayonnement de fond cosmologique que croyaient, à tort, avoir détectés en 2014 les scientifiques de l'expérience BICEP2BICEP2. À cela s'ajoute, pour former le fond stochastique proprement dit, la somme incohérente des émissions gravitationnelles de toutes les sources astrophysiques standards (voir plus loin) existant dans l'universunivers observable, mais indiscernables individuellement.
Malgré le caractère aléatoire que présentent toutes ces sources, il convient de noter qu'elles correspondent à des fréquences bien plus basses que celles des sources astrophysiques aujourd'hui les plus intéressantes d'un point de vue ondes gravitationnelles et ne sont donc pas vraiment gênantes pour les détecteurs actuels. Par exemple, le bruit de fond cosmologique pourra tout au plus être "contraint" par la plupart des détecteurs s'intéressant à des sources plus intenses. Cependant, l'une des ambitions de la NASANASA est de développer dans le futur un programme de détecteurs (Le Big Bang Observer) encore plus gigantesques que le plus grand actuellement en cours de réalisation (le projet eLISA dont un prototype sous une forme simplifiée, LISALISA Pathfinder, a été mis en orbiteorbite début décembre 2015), et ce afin d'essayer de percer, grâce aux ondes gravitationnelles primordiales, les mystères du Big Bang.
2) Sources catastrophiques
Cette catégorie est assez vaste et regroupe tous les événements astrophysiques mettant en jeu des objets compacts dont l'évolution change brutalement. Sans entrer dans les détails, on peut citer les "coalescencescoalescences" (= collision après un ballet keplerien, voir plus loin) de binaires (couples de deux objets dont l'un, au moins, est une étoile à neutronsétoile à neutrons ou un trou noirtrou noir), les effondrements en trous noirs d'étoiles à neutrons ou autres objets, les brisures de symétrie dans des objets compacts en rotation (brisure soudaine de l'écorce externe d'une étoile à neutrons par exemple), l'absorptionabsorption d'étoiles par un trou noir supermassiftrou noir supermassif ou encore les supernovae. Il faut cependant noter pour ces dernières que, contrairement à ce que l'on a longtemps cru, l'effondrement étant quasiment sphérique et l'énergie principalement émise sous forme de neutrinosneutrinos, le signal gravitationnel attendu est assez faible.
Toutes ces émissions ont en commun le fait d'être localisées en un point de l'Univers et d'avoir lieu à un instant donné de manière "éruptive". Par ailleurs, l'observation précise de chacune d'entre elles permettrait certes d'avoir des contraintes supplémentaires tant sur les équations d'état de la matièreétat de la matière que sur la "vraie" théorie de la gravitation, l'inconvénient étant toutefois qu'il faut regarder au bon endroit au bon moment. Les sources plus régulières, bien que créant généralement des ondes d'amplitudes moindres, sont donc peut-être plus intéressantes si l'on dispose de longues observations suffisamment sensibles. Et ce d'autant plus que leur régularité permet justement l'emploi de "filtres" lors de l'analyse du signal. Les coalescences de binaires de trous noirs restent néanmoins le meilleur candidat pour les premières générations de détecteurs.
3) Sources périodiques
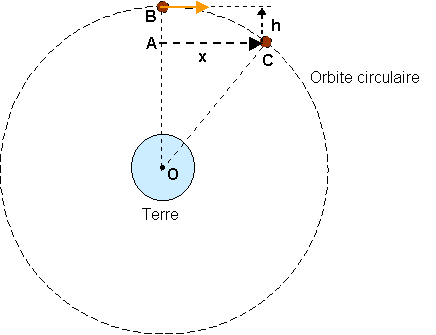
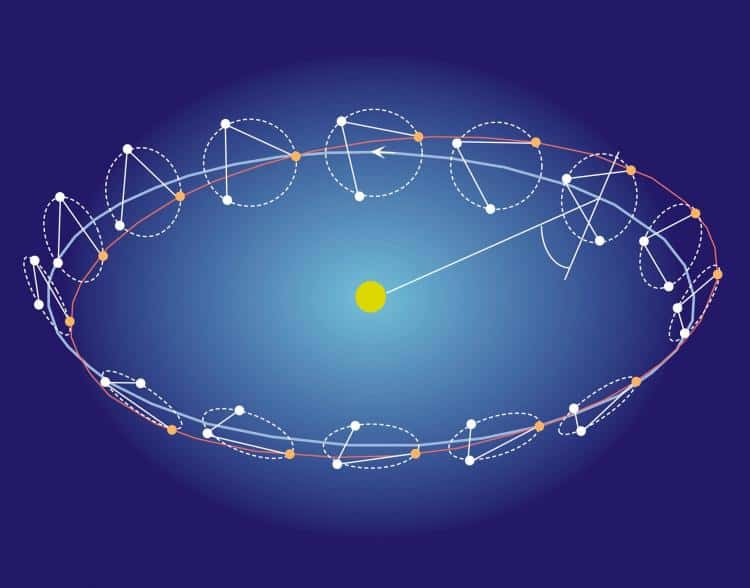
Selon la relativité générale, les binaires compactes (couples d'étoiles à neutron, par exemple), qui sont en orbite "l'une autour de l'autre", forment des sources périodiques mais faibles de rayonnement gravitationnel. Cette prédiction fut vérifiée de manière spectaculaire grâce à l'observation longue et minutieuse du pulsarpulsar PSR B1913+16, par les astrophysiciensastrophysiciens américains qui le découvrirent en 1974, Russell Hulse et Joseph Taylor. Ceux-ci démontrèrent ainsi que ce pulsar fait partie d'un système binaire dont l'autre membre est également une étoile à neutrons, ce qui implique que l'ensemble est un système compact. Alors que dans le cas du système formé de MercureMercure et du Soleil, l'effet de la relativité générale est presque uniquement de faire "tourner" l'orbite elliptique de Mercure, dans le cas du système binaire, le fait que l'espace-temps soit lui-même dynamique intervient dans le fait que ce système perd de l'énergie émise sous forme d'ondes gravitationnelles. De cette façon, les deux étoiles se rapprochent sans cesse l'une de l'autre, la période du mouvement changeant légèrement avec le temps. La très grande précision des mesures de Taylor et Hulse (qui leur valurent le prix Nobel en 1993) est illustrée sur la figure suivante, qui présente également en trait plein la prédiction de la relativité générale. Ainsi, cette longue observation représente un très bon test pour la relativité générale, puisque l'accord avec celle-ci est parfait, et même si elle ne rejette pas complètement toutes les théories alternatives de la gravitation, elle les contraint tout de même très fortement.
 |
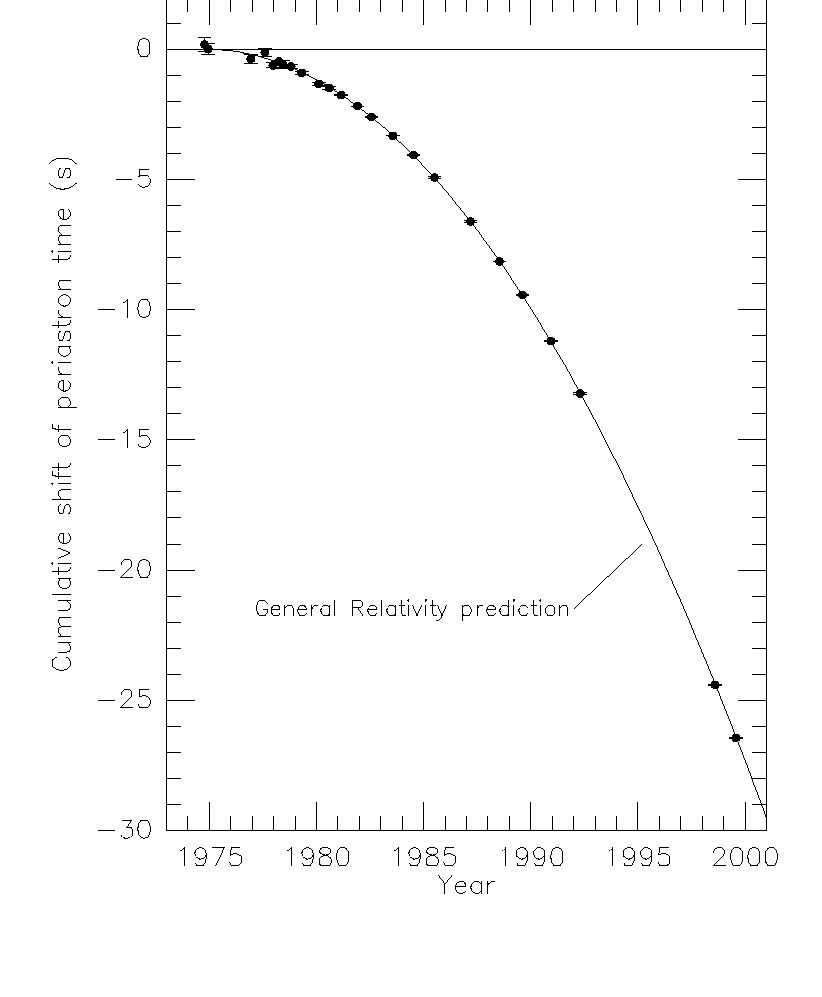 |
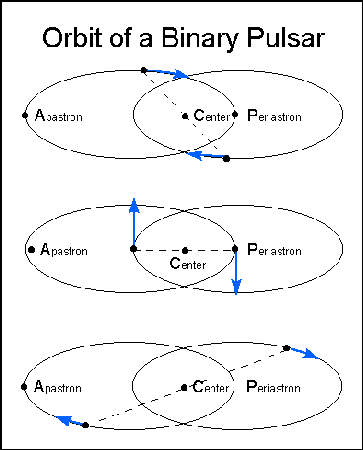
Au-dessus, illustration des orbites des deux étoiles du système binaire découvert par Taylor et Hulse. En dessous, décroissance de la période orbitalepériode orbitale du pulsar binaire PSR B1913+16 mesurée par le décalage du passage au périastrepériastre par rapport au cas d'une orbite de période constante (cliquez pour agrandir). La courbe en trait plein est la prédiction faite par relativité générale et les points sont les mesures expérimentales réparties sur plus de 20 ans. Grâce à la très longue observation, les barres d'erreur expérimentales les plus récentes sont moins larges que le trait de la courbe. Sources M. Haynes et Lorimer (2001). |
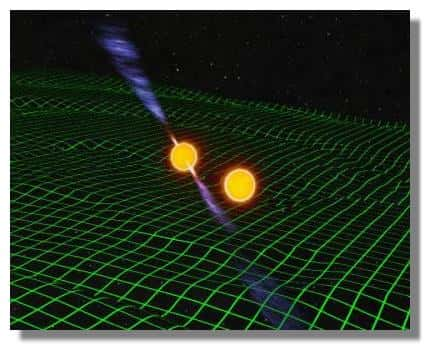
Par ailleurs, cette lente évolution résulte, après des millions d'années d'émission lente et régulière d'ondes gravitationnelles, en la collision des deux étoiles à neutrons (événement mentionné précédemment comme l'une des "sources catastrophiques d'ondes gravitationnelles") et la formation d'un trou noir. Ce scénario est illustré par les figures suivantes, avec des hyperliens vers des animations (attention : taille de quelques megabytes, format mpeg). Il faut noter que ce scénario astrophysique étant fort complexe (autant à cause de la relativité générale que de la physique nucléaire à hautes densités, qui intervient dans la description de la composition des étoiles à neutrons), ces animations ne sont pas complètement réalistes, mais elles donnent cependant les traits principaux de cette évolution et de sa fin explosive.
 |
 |
Illustration de l'évolution d'un système binaire similaire à celui découvert par Taylor et Hulse. Les deux étoiles à neutrons exécutent un balai (au-dessus), qui finit par leur coalescence (en dessous) sous la forme d'un trou noir, toute cette évolution générant d'abord un rayonnement gravitationnel faible mais continu, puis un "flashflash" très court mais bien plus intense. Source NASA, cliquez pour accéder aux animations par John Rowe. |
En ce qui concerne l'observation directe d'ondes gravitationnelles dans un avenir proche, contrairement à ce qu'il en est pour la phase finale (qui pourrait être observée même en dehors de notre galaxiegalaxie), un système tel que le pulsar PSR B1913+16 dans sa phase actuelle (en évolution très lente) n'est pas détectable pour deux raisons distinctes, mais corrélées. De telles binaires émettent des signaux d'amplitudes très faibles (et devraient donc être situées relativement près de nous dans la Voie LactéeVoie Lactée pour pouvoir donner des signaux observables), qui ont de plus des fréquences bien trop faibles pour les détecteurs opérationnels. Pour avoir des sources qui soient périodiques, tout en produisant des ondes d'amplitudes plus importantes, on peut donc s'intéresser à des objets encore plus compacts, comme des étoiles à neutrons ou des trous noirs isolés en rotation. Si, pour une étoile à neutrons, la rotation est accompagnée d'une asymétrie axialeaxiale, on a en effet un moment quadrupolaire de masse variant dans le temps. Il faut cependant que cette asymétrie dure suffisamment longtemps par rapport à la période de rotationpériode de rotation de l'objet. Parmi les mécanismes aptes à créer de telles asymétries de manières stationnaires, ont été proposées l'existence d'une déformation locale de l'écorce cristalline d'une étoile à neutrons, ou encore l'existence une déformation globale provoquée par la tension due à un intense champ magnétiquechamp magnétique.
Finalement, on a aussi suggéré la possibilité de déformations qui soient variables dans le temps, i.e. des oscillations. Dans le cas des trous noirs, il a été montré, autant pour le trou noir de Schwarzschild (sans rotation) que pour celui de Kerr (en rotation), que les oscillations n'ont que de très courtes durées de vie (on parle d'ailleurs de QPO, quasi-periodic oscillations, plutôt que d'oscillations proprement dites). Un trou noir "déformé" émet, en quelques millisecondes, toute l'énergie due à cette déformation sous forme d'ondes gravitationnelles, afin de devenir rapidement stationnaire et avec une surface "lisse", en accord avec le théorème selon lequel ils n'ont pas de cheveux. En revanche, les oscillations d'objets compacts faits de matière, tels que les étoiles à neutrons, se sont révélées beaucoup plus intéressantes, pouvant durer de "longues" secondes, ou bien plus encore, si l'étoile est dans un système binaire et qu'elle accrète de la matière volée à son compagnon. Les ondes gravitationnelles générées par ces oscillations seront peut-être détectées dans un futur proche, même s'il est quasi-certain que les premières observations viendront plutôt des dernières étapes de la coalescence de trous noirs binaires en un trou noir encore plus massif.
C - La détection directe des ondes gravitationnelles
Vingt-trois ans à peine séparent le moment où Maxwell prédit l'existence d'ondes électromagnétiques (1864) de celui où Hertz les mit en évidence expérimentalement (1887). En revanche, même si Einstein montra dès 1916 que sa théorie relativiste de la gravitation prévoyait un phénomène semblable, à savoir la possibilité d'oscillations du champ de gravitation se propageant à la même vitesse que la lumière, les ondes gravitationnelles n'ont toujours pas été directement observées en 2004. Néanmoins, les efforts pour essayer de les détecter ont commencé dans les années 1960, sous l'impulsion du physicien américain Joseph Weber, et il existe aujourd'hui plusieurs télescopestélescopes gravitationnels opérationnels ou en fin de constructionconstruction. Ainsi, il est désormais raisonnable de croire que la première détection directe d'une onde gravitationnelle devrait avoir lieu dans un futur assez proche.
Les raisons pour lesquelles il y a une telle différence entre l'histoire des ondes gravitationnelles et celles des ondes électromagnétiques sont multiples, mais fort instructives sur ces théories. En effet, l'une de ces raisons est que même si toutes deux entrent dans le cadre des théories de jaugethéories de jauge, la relativité générale semble bien souvent plus exotiqueexotique par la façon dont elle brusque les concepts qui étaient auparavant a priori bien établis d'espace et de temps, concepts qui avaient déjà été "violentés" par sa petite soeur, la relativité restreinterelativité restreinte. Cette caractéristique fut probablement à l'origine de la longue période qu'il fallut à la communauté scientifique pour admettre la relativité générale, bien qu'Eddington vérifia dès 1919 l'une de ses principales prédictions. Mais en plus de remettre en cause les idées reçues sur l'espace et le temps, la relativité générale fait appel à un formalisme mathématique qui n'était alors pas encore répandu dans la communauté des physiciens : la géométrie différentielle. Ces deux difficultés combinées rendent assez compréhensible la réticence vis-à-vis de la relativité générale dont firent preuve les scientifiques n'en maîtrisant pas parfaitement les fondements. Et ce d'autant plus que les spécialistes eux-mêmes restèrent longtemps partagés sur la validité de certaines prédictions, telles celle de l'existence de "singularités" de l'espace-temps (les trous noirs), de l'expansion de l'Univers, ou encore des ondes gravitationnelles. Dans ces trois cas, il fallut attendre près de cinquante ans après la naissance de la théorie pour que la réalité physique des phénomènes soit définitivement admise. Ainsi, aujourd'hui, le dernier obstacle à la détection des ondes gravitationnelles reste le défi technologique que représente une telle observation. Ici réside en effet une autre grande différence entre la théorie d'Einstein et celle de Maxwell, différence qui a été signalée lors de la description des conditions nécessaires pour l'émission d'ondes gravitationnelles : autant l'émission ou la détection d'un signal électromagnétique peuvent être facilement réalisées naturellement ou artificiellement, autant un signal gravitationnel intense exige de grands moyens de la part des scientifiques ou de la Nature pour être émis ou capté.

Il existe ainsi deux grands types de détecteurs artificiels, auxquels s'ajoute une méthode de détection alternative plus récente qui utilise des masses tests naturelles. Parmi les détecteurs, on distingue les "acoustiques", le principe desquels est de regarder les vibrations d'un ensemble continu de points matériels, et les "interférométriques", où l'on mesure plutôt les distances entre au moins quatre masses qui sont les miroirsmiroirs d'un interféromètre de Michelsoninterféromètre de Michelson. La stratégie à part est celle du consortium IPTA (International Pulsar Timing Array, réseau international de chronométrage de pulsars) qui propose de mettre en évidence les ondes gravitationnelles à l'aide d'une trentaine de pulsars, lesquels sont en pratique des horloges extrêmement stables mais dont l'observation peut être perturbée par le passage d'une onde.
- Détecteurs acoustiques
La première "barre résonnante" fut celle de Weber. Il y en eut depuis plusieurs, dont certaines sont toujours en service, voire en projet. Ce sont typiquement des barres cylindriques (par exemple EXPLORER au CERNCERN, ALLEGRO en Louisiane) ou des sphères (par exemple GRAIL à Leiden) d'environ deux tonnes de métalmétal et dont la matière et la masse sont choisies afin que la vitesse du sonvitesse du son dans la barre implique des fréquences propres de l'ordre du kHz, valeurs typiquement attendues pour les sources astrophysiques. Par ailleurs, les versions modernes de ces barres sont refroidies à des températures de l'ordre du kelvinkelvin ou même inférieures, afin de diminuer les parasites liés aux fluctuations thermiques. Le principal inconvénient de ce type d'expérience est que les signaux pouvant être détectés doivent avoir quasiment les mêmes fréquences que les modes propres d'oscillation des solidessolides (aux alentours du kHz). Leur grand avantage est leur faible coût, en tous cas comparativement aux télescopes interférométriques, ce qui permet facilement d'envisager de faire des réseaux. On augmente ainsi la "section efficace" (=la proportion du ciel qui est observée) et, pour les cylindres, on acquiert l'avantage que présentent les sphères : l'absence de direction privilégiée qui assure de mieux localiser la source.
- Interféromètres

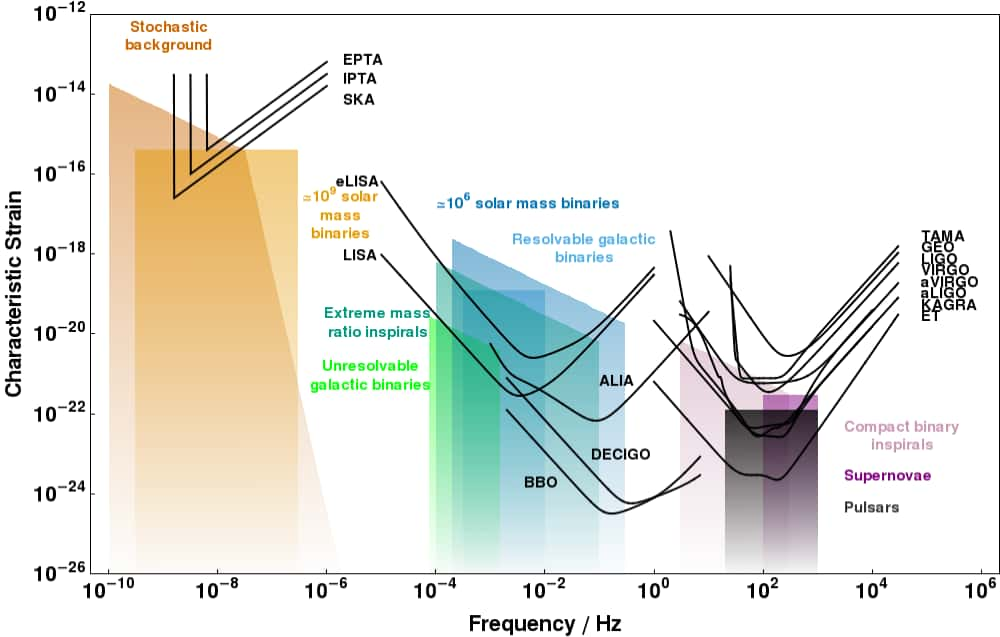
Toutefois, le principal avantage des interféromètres est leur large bande passantebande passante, allant de 10 Hz à quelques kHz pour les expériences terrestres et de 10-3 à 0.1 Hz pour eLISA. Comme le montre la figure suivante illustrant la sensibilité pour VIRGO, le bruit à basses fréquences est surtout d'origine sismique. Un projet spatial comme eLISA est donc la meilleure possibilité pour explorer ce domaine du spectrespectre, qui correspond par exemple aux coalescences de systèmes binaires massifs ou au bruit de fond cosmologique (voir la figure avec la comparaison entre les sensibilités des divers détecteurs). La courbe de sensibilité de VIRGO montre aussi que l'un des principaux bruits à hautes fréquences est la fluctuation d'origine quantique du nombre de photons dans les laserslasers, un point qui illustre assez bien la très haute technicité des télescopes gravitationnels. Malgré tout, la dernière figure révèle que beaucoup de progrès ont été faits depuis la première génération de détecteurs et que nous ne sommes peut-être plus très loin d'une détection directe, en tous cas pour les ondes émises par des binaires compactes stellaires.
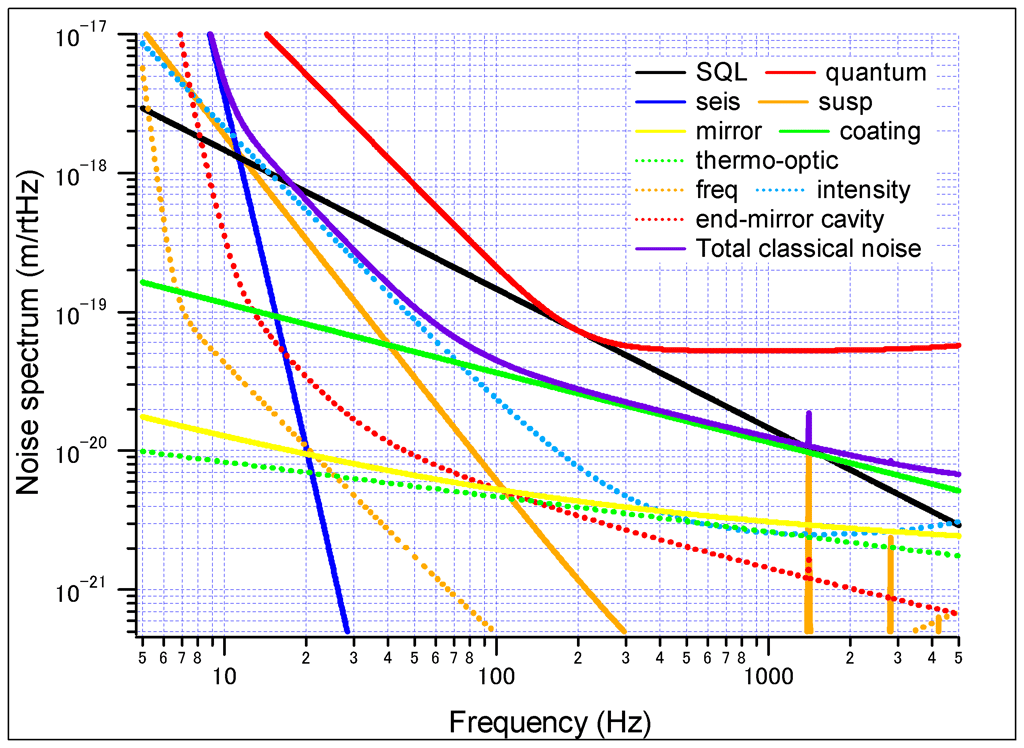
Cliquez pour agrandir. Au-dessus, courbe de sensibilité du détecteur LIGO, illustrant quelques unes des nombreuses sources de bruits dont il doit être isolé le mieux possible. À basses fréquences, il s'agit avant tout du bruit sismique (vibrations du sol) et à hautes fréquences d'effets quantiques liés aux fluctuations des lasers. En dessous, schéma de l'interféromètre VIRGO, dont les bras, afin d'avoir des longueurs efficaces plus grandes, sont des cavités Fabry-Perot. Sources Osservatorio di Arcetri, IN2P3/INFN. |
Avec ces divers détecteurs gravitationnels, le but n'est donc plus réellement de tester la théorie d'Einstein de la gravitation relativiste, mais avant tout de disposer de "télescopes gravitationnels". L'espoir, très probablement fondé, est que ceux-ci révolutionnent notre perception de l'Univers, de la même façon que les observations électromagnétiques des sources X ou gamma ont autrefois considérablement élargi notre vision. Toutefois, autant le rayonnement électromagnétique repose sur une théorie bien établie (celle de Maxwell), autant la "lumière gravitationnellelumière gravitationnelle" pourrait nous réserver des surprises, étant donné que la théorie de la relativité générale, bien qu'ayant passé avec grand succès de nombreux tests, a de multiples raisons de ne plus être valable à plus hautes énergies et/ou dans des situations où le champ de gravitation devient bien plus intense. Mais si une telle découverte était faite, elle n'étonnerait probablement pas tout le monde, les théories cherchant à élargir la relativité générale étant aujourd'hui très nombreuses, parmi lesquelles la théorie des membranes (descendante des théories de supercordes) et la "loop quantum gravityloop quantum gravity", sujets parmi ceux qui sont très brièvement abordés en guise de conclusion de ce dossier.
1 une distance d'un megaparsec (= un million de parsecsparsecs) représente environ 3. 1022 mètres, soit deux fois la distance qui sépare la Voie Lactée de sa plus proche voisine, la galaxie d'Andromèdegalaxie d'Andromède.
2 On note que contrairement au cas de l'amplitude d'une onde électromagnétique, celle d'une onde gravitationnelle décroît proportionnellement à la distance et non au carré de celle-ci, ce qui est probablement la seule caractéristique de ces ondes rendant le cas gravitationnel plus aisé.