au sommaire

Le renouveau de la relativité générale : les astres compacts
A - Trous noirs et autres astres compacts

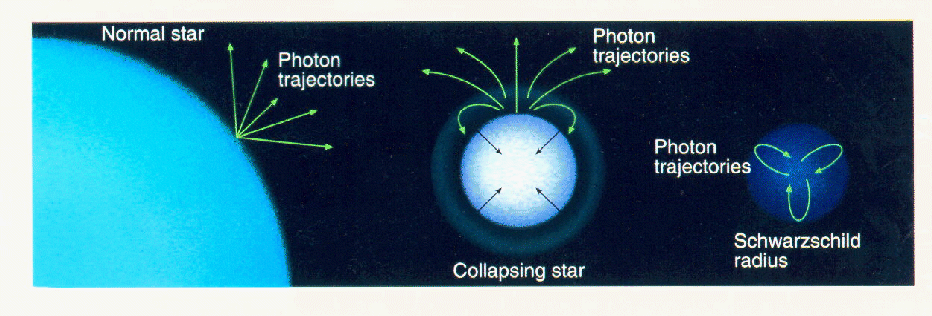
Michell fut l'un des premiers à réfléchir aux conséquences d'une influence possible de la gravitation sur la lumière, et à suggérer que les particules de lumière pourraient être elles aussi attirées par un objet massif, comme toute autre particule. Partant de cette hypothèse, il conclut que, puisque plus un objet est massif, plus il faut une vitessevitesse grande pour lui échapper, les étoilesétoiles les plus massives devaient être invisibles, la lumière qu'elles émettent ne pouvant pas échapper à leur attraction (en termes modernes, on dit que la "vitesse de libération" est supérieure à celle de la lumière). La proposition de Michell était cependant trop en avance sur son temps, et elle parut complètement dénuée d'intérêt aux membres de la Royal Society. Ses idées restèrent donc oubliées de tous, excepté de Laplace qui, quelques années plus tard, fit une proposition similaire dans son Exposition du Système du Monde. Le concept de trou noir était né, sous le nom "d'astre occlus", néanmoins, pour devenir célèbre et reconnu, il dut naître à nouveau, au XXème siècle, sous une forme légèrement modifiée et découlant de la relativité générale.
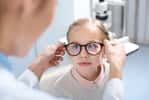
Mais avant d'en arriver précisément à la relativité générale, il est intéressant de s'attarder un peu sur le raisonnement newtonien de Michell qui, de manière assez intrigante, donne des prédictions très similaires à celles de l'étude des trous noirs dans le cadre de la relativité générale. Ainsi, si l'on cherche à estimer, dans le cadre de la théorie de NewtonNewton, le rayon que doit avoir un astre de masse M pour que même la lumière émise à sa surface ne puisse s'en échapper, on trouve une valeur qui est proportionnelle à la masse M, et nommée depuis le XXème siècle "rayon de Schwarzschildrayon de Schwarzschild", Rs, du nom de l'Allemand Karl Schwarzschild. On a :
Rs = 2 G M / c²
où G est la constante de Newton, c la vitesse de la lumièrevitesse de la lumière dans le vide et M la masse de l'objet.
La conclusion qui ressort de ce calcul (et qui fut celle de Michell) est que si un astre de masse M donnée a un rayon inférieur au rayon de Schwarzschild qui correspond à sa masse, alors même la lumière devrait ne pas pouvoir sortir de son voisinage proche. En pratique, ce qui permet de décider si cette condition est vérifiée est donc le rapport entre le rayon de Schwarzschild de l'objet et son rayon, ce que l'on nomme son paramètre de compacité, et qui est proportionnel au rapport entre sa masse et son rayon. Or, il s'avère que la même condition apparut en relativité générale en 1916, toutefois, sans que l'idée de Michell ne soit initialement rattachée à la "solution de Schwarzschild".
 |
 |
Ainsi, le renouveau du concept d'astre occlus commença quelques mois à peine après la publication par EinsteinEinstein des équationséquations de la relativité générale, lorsque Schwarzschild, quelque part sur le front russe, découvrit la première solution exacte connue de ces équations1. Cette solution décrit, dans le vide, le champ gravitationnel sphérique entourant un corps de masse M, et appliquée au cas du champ gravitationnel autour du SoleilSoleil2, elle permit de faire le calcul exact de la déviation de la lumière, calcul qu'Einstein n'avait fait que de manière approchée, obtenant néanmoins le bon résultat. Par ailleurs, Hans Reissner trouva quelques mois plus tard la généralisation de cette solution au cas où le corps de masse M porteporte aussi une charge électrique Q, solution redécouverte peu après indépendamment par Nordström. Cette solution de Reissner-Nordström, dont l'existence traduit le fait que l'énergieénergie électromagnétique associée à la charge électrique apporte une source supplémentaire de courbure de l'espace-tempsespace-temps, passa cependant presque inaperçue, même si elle conduit naturellement au "trou noir de Reissner-Nordström". En effet, à cette époque, l'attention des gens était en grande partie focalisée sur certaines propriétés de la solution de Scharzschild, parmi lesquelles le fait que pour tout corps de masse M, il existe une valeur de la coordonnée radiale pour laquelle le coefficient "temporel" de la métrique3 s'annule alors que le coefficient "purement radial" devient infini. On parle de l'apparition d'une "singularité" dans la métrique, phénomène qui se produit lorsque la coordonnée radiale devient égale au rayon de Schwarzschild associé à la masse M source du champ.
Ces détails furent rapidement notés autant par Schwarzschild lui-même que par Einstein, et laissaient les gens un peu perplexes, certains prétendant toutefois que la question n'était pas si importante que ça, puisque la valeur du rayon de Schwarzschild était extrêmement faible pour les astres connus alors (voir le tableau). Leur raisonnement était de dire que dans tous les cas physiquesphysiques, la sphère sur laquelle la métrique devient singulière est située bien à l'intérieur de l'objet (la Terre, le Soleil ou toute autre étoile), or, la métrique de Schwarzschild ne s'y applique plus car elle n'est valable que dans le vide. Cette argumentation était d'ailleurs défendue par le fait que la métrique devient également singulière à l'origine (quand la coordonnée radiale s'annule), ce qui est similaire à ce qui se passe en gravitation newtonienne, où cela ne pose aucun problème. En effet, même si le champ newtonien créé par une masse ponctuelle est infini là où est la masse (à l'origine), la solution mathématique peut malgré cela être utilisée pour décrire le champ gravitationnel créé par les planètes là où elle est valable : dans le vide, à l'extérieur de celles-ci. A l'intérieur des planètes, la solution est différente et ne diverge pas. Suivant ce fil de pensée, on pouvait ainsi se dire que la situation en relativité générale devait être la même, les problèmes de singularités dans la métrique de Schwarzschild restant purement mathématiques sans avoir la moindre implication physique.
Néanmoins, cette idée déplaisait, avec raison, à d'autres pour qui la singularité sur la surface de rayon égal au rayon de Schwarzschild était un problème bien différent de la singularité à l'origine. Même si l'on pouvait raisonnablement douter de l'existence de masses ponctuelles, rien ne pouvait a priori exclure l'existence d'étoiles de rayons plus petits que leurs rayons de Schwarzschild. Au contraire même, on avait découvert en 1862 la première "naine blanchenaine blanche" (SiriusSirius B), étoile de masse similaire à celle du Soleil, mais dont la luminositéluminosité et la température indiquaient que sa taille était bien inférieure, son diamètre étant de l'ordre de celui de la Terre. Plus génant encore, avec l'avénement de la physique quantiquephysique quantique, le physicienphysicien britannique R.H. Fowler démontra en 1926 que, contrairement aux étoiles normales, les naines blanches ne résistaient pas à la gravitation grâce à l'émissionémission d'énergie électromagnétique, mais grâce à la "pression de dégénérescencepression de dégénérescence des électronsélectrons", effet purement quantique. Or, en 1930, le physicien indien Subrahmanyan ChandrasekharSubrahmanyan Chandrasekhar, se reposant sur ce résultat, découvrit que les naines blanches admettaient une masse maximale (nommée depuis "masse de Chandrasekharmasse de Chandrasekhar") au-delà de laquelle elles devaient s'effondrer, ce qui laissait la place libre à des objets encore plus compacts. Parmi ceux-ci, les étoiles à neutronsétoiles à neutrons furent rapidement "inventées", principalement grâce à la découverte, en 1932, du neutron par le physicien anglais James Chadwick. Ainsi, les "étoiles à neutrons" furent indépendament prédites par le physicien russe Lev Landau4, mais aussi par l'Américain Walter Baade et l'Allemand Fritz Zwicky qui, fin 1933, écrivirent dans un résumé de conférence leur désormais très célèbre prédiction "With all reserve, we advance the view that supernovaesupernovae represent the transitions from ordinary stars into 'neutrons stars', which in their final stages consist of extremely closedly packed neutrons." (une traduction : "Avec les précautions qui s'imposent, nous émettons l'hypothèse selon laquelle les supernovae témoigneraient de la transformation d'étoiles normales en 'étoiles à neutrons', celles-ci étant constituées, dans leur état final, de neutrons extrêmement compactés.")
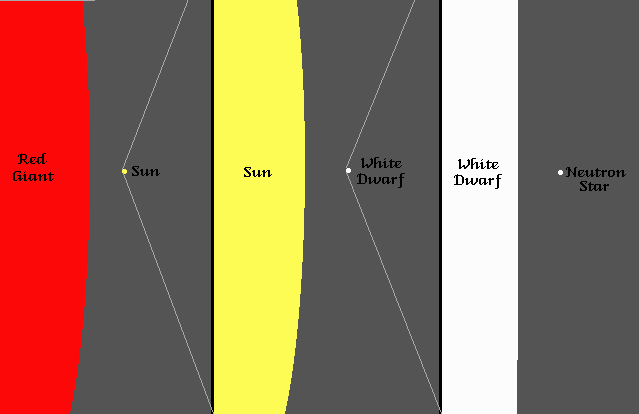 |
| Objet | Terre | Soleil | Naine blanche | Etoile à neutron |
|---|---|---|---|---|
| Masse (en masses solaires) | 0,000 003 | 1 | environ 1 | 1 à 3 |
| Rayon (km) | 6 400 | 700 000 | environ 10 000 | environ 10 |
| Densité (g.cm-3) | 5 | 1 | 107 | 1014 |
| Vitesse de libération (km/s) | 11.3 | 620 | 5 000 | 250 000 |
| Rayon de Schwarzchild | 8 mm | 3 km | 10 km | 6 km |
| Compacité | 10-10 | 0,000 001 | 0,000 1 | 0,2 |
B - Singularité et horizon des événementshorizon des événements
L'idée de Baade et Zwicky selon laquelle l'effondrement gravitationnel d'étoiles massives en fin de vie pourrait donner des objets très compacts fut évidemment reprise pour accréditer l'existence d'objets de rayon inférieur à leur rayon de Schwarzschild. Mais ce ne fut pas suffisant pour que le concept de trou noir s'impose rapidement, suite à l'opposition d'Eddington, qui, très influent dans le domaine relativiste, avait déjà réussi à retarder énormément son acceptation. Par exemple, le fait que la singularité présente sur la surface de Schwarzschild n'est qu'un artefact mathématique avait été démontré à partir de 1921 par diverses personnes, dont le Français Paul Painlevé, l'Anglais Oliver Lodge et Eddington lui-même... Ceux-ci, ainsi que Lemaître en 1934, retrouvèrent sous d'autres formes, la solution de Schwarzschild, formes dans lesquelles il n'y avait plus de singularité sur la sphère de Schwarzschild, ce que notèrent Painlevé, Lodge et Lemaître, mais pas Eddington qui continua donc à refuser ces objets trop "exotiquesexotiques" pour lui.
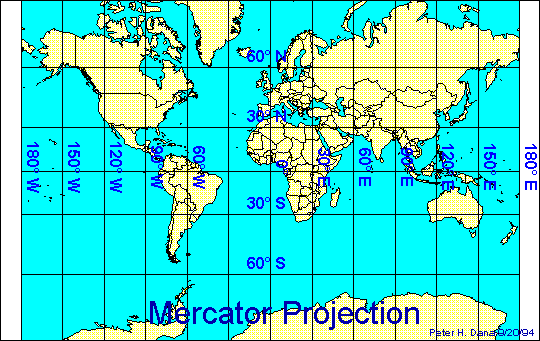
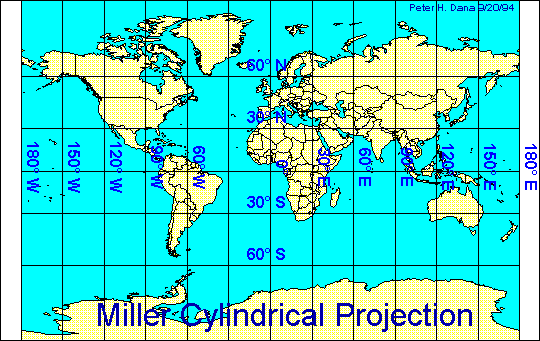
Mais avant de continuer plus en avant cette description historique, il est probablement nécessaire d'expliquer pourquoi diverses personnes purent réobtenir la solution de Schwarzschild, sous des formes qui ne présentaient plus de singularité sur la surface de rayon Rs. Cela fait en effet appel à certains aspects de la relativité générale qui avaient été volontairement assez peu développés dans les chapitres précédents. Ainsi, il a été dit que le principe de relativité généralisé implique que l'élément de longueur local ds² doit rester identique sous tous les changements de coordonnées, et pas seulement les transformations de Lorentz. Ceci signifie que tous les systèmes de coordonnées possibles sont envisageables, avec toutefois la restriction que, localement, ils permettent d'écrire la métrique sous la forme de Minkowski, ce qui est la transcriptiontranscription mathématique du principe d'équivalence : localement, on peut toujours trouver un système de coordonnées dans lequel l'espace-temps est plat. Cependant, un système de coordonnées qui vérifie cette condition n'est jamais unique, et il n'est pas nécessairement valable pour décrire tout l'espace-temps, ce qui est à rapprocher d'un sujet abordé lors de la brève description de la notion de courbure intrinsèque, la représentation sur une carte plane du globe terrestre. De la même manière que toutes les cartes géographiques ne permettent pas de représenter la surface terrestre dans son intégralité, tous les systèmes de coordonnées (qui sont des "cartes mathématiques") ne permettent pas de décrire un espace-temps donné dans son ensemble5. Plus précisément, l'analogieanalogie se comprend bien si l'on réfléchit à la représentation du Pôle Nord et du Pôle Sud sur la plupart des cartes terrestres : ces points sont "sacrifiés" et étalés tels des segments de droites...
 |
 |
La conclusion à retenir de tout ceci est qu'en relativité générale (et cette conclusion s'applique également de manière plus générale au cadre de la géométrie en espace courbe), on peut utiliser n'importe quel système de coordonnées pour décrire un espace-temps donné, mais il faut être très prudent lorsque l'on cherche à trouver des informations physiques au sujet de cet espace-temps. Les systèmes de coordonnées n'ont pas nécessairement de "réalité physique", la plupart n'en ayant même une que localement, là où se trouvent les observateurs qui peuvent facilement "localement effacer" la courbure. Dans un système de coordonnées donné, la variable "t" n'est pas obligatoirement un temps : on peut affirmer que c'en est un uniquement si l'on peut trouver un observateur physique qui aurait comme temps propretemps propre ce que l'on nomme donc un "temps-coordonnée". Et lorsque ce temps est bien le temps d'un observateur, qui est cependant distant du point spatial considéré, le temps permet certes de décrire ce que perçoit à distance cet observateur, mais absolument pas de dire ce que "vivrait" un autre observateur qui serait situé au point spatial en question. De manière générale, seul l'objet "géométrique" espace-temps a une "réalité physique", et non toutes les informations contenues dans les systèmes de coordonnées qui peuvent être utilisés pour le décrire : dans certains systèmes semblent se produire des phénomènes qui n'ont pas d'existence concrète, tel l'étalement des pôles terrestres.
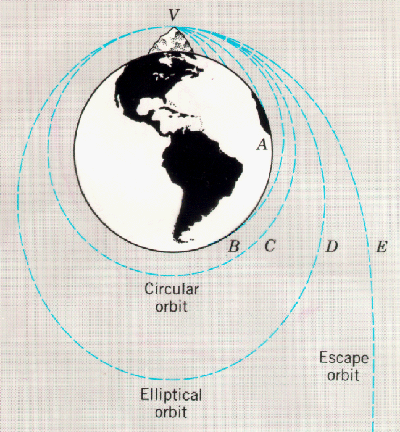
En conséquent, ce qui avait été démontré dès les années 1920-1930 par Painlevé, Lodge et Lemaître, c'était que la sphère de Schwarzschild n'était pas un endroit où l'espace-temps devenait singulier, même s'il s'y passe réellement quelque chose d'étrange. En effet, tous démontrèrent et comprirent que la sphère de Schwarzschild est ce que l'on nomme désormais un "horizon des événements", c'est-à-dire une surface que l'on peut traverser uniquement dans une seule direction. La raison pour laquelle la métrique décrite en coordonnées de Schwarzschild présente une singularité sur l'horizon vient du fait que ce système de coordonnées est adapté à des observateurs qui restent à distance constante de cet horizon, par exemple à l'infini. Or, plus on approche de l'horizon, plus il devient difficile de rester immobile par rapport à lui, et c'est même impossible, par définition, là où il se trouve. Si l'on considère un observateur pour lequel le système de coordonnées découvert par Schwarzschild est valable, et qui est donc au repos par rapport à l'horizon, il constate divers phénomènes contre-intuitifs. Par exemple, en regardant un autre observateur chuter librement dans le trou noir, il le voit s'approcher de plus en plus lentement de l'horizon, tout en devenant de moins en moins brillant, de plus en plus rouge et de plus en plus étiré. Les deux premiers effets viennent de la dilatationdilatation temporelle résultant de la forte courbure de l'espace-temps que génère le trou noir, le deuxième étant lié au fait que de moins en moins de photonsphotons parviennent à l'infini par "unité de temps-coordonnée", même si la source (= l'observateur en chute) continue à en émettre autant par "seconde mesurée près de l'horizon". Le troisième est quant à lui un exemple de l'effet Einstein, décalage vers le rougedécalage vers le rouge de la lumière émise dans un endroit où le champ gravitationnel est plus fort vers un endroit où il est plus faible. Finalement, l'étirement est lié à l'effet de maréemarée, et provient du caractère non-uniforme du champ gravitationnel. On note d'ailleurs que cet effet de marée près de l'horizon est d'autant plus prononcé que le trou noir est petit. Le résultat global de tout ceci est que les observteurs restant infiniment éloignés du trou noir ne verront jamais l'observateur qui chute passer l'horizon, mais celui-ci, une fois "près" de l'horizon, deviendra néanmoins invisible pour eux en un temps très court (on montre que l'intensité lumineuse baisse de manière exponentielle). De plus, selon son temps à lui, cet observateur chutant dans le trou passera l'horizon en une duréedurée finie, et savoir s'il y survivra dépend avant tout de la force des effets de marée et donc de la masse du trou noir. De toutes façons, il finira très rapidement par rencontrer la singularité « centrale » dont le statut "physique" (dans le cadre de la relativité générale) fut démontré par Hawking et Penrose au cours des années 1970 (voir plus loin), rencontre à laquelle il ne survivra pas puisqu'il s'agit d'une région de l'espace-temps où la courbure devient "infinie"6. La présence de cette singularité interne, qui pourrait disparaître dans le cadre d'une description quantique de la gravitation, illustre les limites de la relativité générale tout en soulevant cependant des difficultés plus profondes que les infinis qui apparaissent en physique newtonienne pour une masse ponctuelle. En effet, il ne faut a priori pas la visualiser comme une sorte de point de l'espace où se concentrerait la matièrematière qui tombe dans le trou noir, mais plutôt en quelque sorte comme un instant où la notion d'espace-temps cesse d'avoir un sens. Il est par exemple parfaitement possible que deux particules passées à travers l'horizon d'un trou noir rencontrent la singularité au même instant mais en des endroits différents.
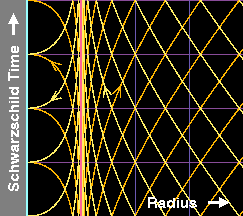
Certains des effets qui viennent d'être décrits ici peuvent être observés sur les figures suivantes. La première d'entre elles représente l'espace-temps (à une dimension d'espace et une de temps pour simplifier) à proximité de l'horizon d'un trou noir, selon un observateur de Schwarzschild, c'est-à-dire qui reste immobile par rapport à l'horizon. Les lignes qui correspondent, à l'extérieur, à l'espace à un instant donné pour cet observateur, sont horizontales et violettes. Inversement, les lignes verticales sont quant à elles les courbes qui gardent une même valeur de la coordonnée « radiale » et décrivent donc, à l'extérieur du trou noir, un lieu donné pour cet observateur qui reste à une distance fixe de l'horizon, lequel apparaît sous la forme d'une ligne verticale rouge. D'autre part, en jaune sont représentées les lignes d'UniversUnivers des particules de masses nulles qui délimitent par conséquent la surface des cônescônes de lumière (s'approchant ou s'éloignant du trou noir). L'existence de la singularité sur l'horizon apparaît dans la "condensationcondensation" de ces lignes d'Univers qui, près de l'horizon, deviennent de plus en plus verticales, ne le franchissant jamais, même venant de l'extérieur, ce qui traduit que l'observateur lointain ne voit jamais la lumière entrer dans un trou noir. Par ailleurs, le fait que les coordonnées de Schwarzschild ne sont pas adaptées à tout l'espace-temps apparaît aussi dans la présence de nouvelles lignes d'Univers pour les photons à l'intérieur du trou noir qui sont déconnectées des lignes externes (tout en semblant avoir un sens du temps inversé). Une fois franchi l'horizon, les choses se compliquent encore puisque, par exemple, les courbes verticales décrivent l'espace interne au trou noir à un « instant donné » et non plus une position à tous les instants, ce qui ne fait que confirmer que les coordonnées ont perdu leur sens. Par exemple, la singularité centrale est l'axe cyan tout à fait à gauche mais, comme on l'a vu auparavant, elle ne doit pas être imaginée comme un point de l'espace.
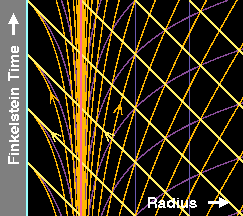
Ces problèmes sont absents de la deuxième figure, qui représente le même espace-temps, mais vu selon un observateur de Eddington-Finkelstein7. Un tel observateur découpe l'espace de la même façon que celui de Schwarzschild (on note les mêmes courbes verticales cyan, rouge et bleues), mais son temps est défini d'une manière telle qu'il reste physique, même une fois l'horizon passé. Cette caractéristique est visible dans le fait que sur cette deuxième figure, les lignes d'Univers délimitant les cônes de lumière entrants dans le trou noir restent orientées à 45 degrés (car les unités sont telles que la vitesse de la lumière est égale à 1), même à l'intérieur du trou noir. Avec les coordonnées de Schwarzschild, cela n'était le cas qu'à l'extérieur, loin de l'horizon. De plus, le fait que l'horizon du trou noir est bien un "horizon des événements", une surface qui ne peut être franchie que dans un sens, ressort du fait que les cônes de lumière sortants (oranges) deviennent de plus en plus verticaux, ceux situés à l'intérieur du trou noir étant attirés vers la singularité centrale au même titre que les cônes entrants. Finalement, la troisième figure (animée) aide à faire le lien entre ces deux systèmes de coordonnées, les lignes à temps de Schwarzschild constant étant lentement déformées pour perdre leur horizontalité et prendre l'allure qu'elles ont dans le système de coordonnées d'Eddington-Finkelstein. En quelque sorte, le système de coordonnées de Schwarzschild décrit l'espace-temps uniquement tel qu'il est vu par des observateurs qui restent distants et ne perçoivent pas l'intérieur du trou noir, alors que celui d'Eddington-Finkelstein est associé à des observateurs qui franchissent l'horizon et explorent donc en partie l'intérieur.
 |
 |
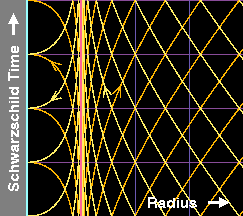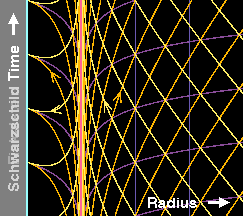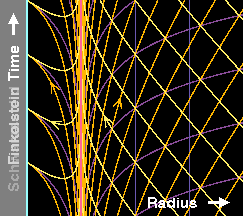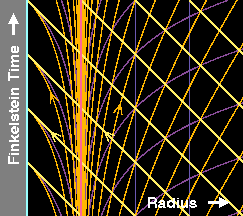 |
Géométrie de l'espace-temps de Schwarzschild (réduit à une seule dimension spatiale) illustrée en coordonnées de Schwarzschild et en coordonnées d'Eddington-Finkelstein. Ces dernières permettent de mettre en évidence le fait que l'horizon n'est pas une surface sur laquelle la géométrie devient divergente, mais uniquement un "horizon des événements", surface qui ne peut être franchie que dans une seule direction. Voir le texte pour plus de détails. Source A. Hamilton. |
C - Vers la découverte des trous noirs et des étoiles à neutrons
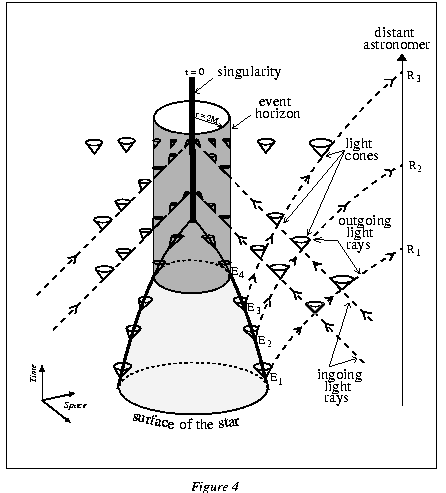
Toutefois, avant que de telles "analyses" ne soient réellement considérées comme physiques et que les "trous noirs" ne méritent l'appelation inventée pour eux en 1967 par le physicien américain John Wheeler, le concept de trou noir eut encore à attendre que l'idée d'effondrement gravitationnel proposée par Baade et Zwicky soit mieux étudiée et qu'Eddington cesse de lutter contre l'acceptation des objets astrophysiques compacts. Un important pas dans cette direction fut, en 1939, le premier calcul relativiste de l'effondrement gravitationnel d'une sphère fluide de poussière (= fluide sans pression) réalisé par les Américains Robert Oppenheimer et Hartland Snyder. Modélisant ainsi l'effondrement d'une étoile, ils montrèrent que, dans ce modèle, l'effondrement donnait lieu à l'apparition d'un horizon des événements coupant l'intérieur du reste de l'Univers. Mais à cause de leur "choix" de négliger la pression, ce résultat ne fut à l'époque pas considéré comme probant, la plupart des physiciens (Oppenheimer inclu) pensant que la pression pouvait changer le résultat. Avec la guerre, la communauté scientifique fut appelée à diverses autres occupations, et la question de l'existence des étoiles effondrées ne revint véritablement à l'ordre du jour que vers 1955, lorsque, en URSS comme aux USA, les physiciens responsables de la modélisationmodélisation numériquenumérique du mécanisme des bombes à hydrogènehydrogène décidèrent d'utiliser également leurs "nouveaux jouets" pour modéliser l'effondrement gravitationnel d'une étoile de manière réaliste. De cette façon, John Wheeler (USA) et Yakov Zeldovich (URSS) démontrèrent qu'Eddington (décédé en 1944) s'était trompé et que le modèle d'Oppenheimer et Snyder faisait la bonne prédiction, malgré son extrême simplicité. A partir de cette époque (fin des années 1950, début des années 1960), l'histoire des trous noirs et celle de "l'astrophysique relativiste" accélérèrent simultanément du fait de plusieurs découvertes théoriques et observationnelles.
 |
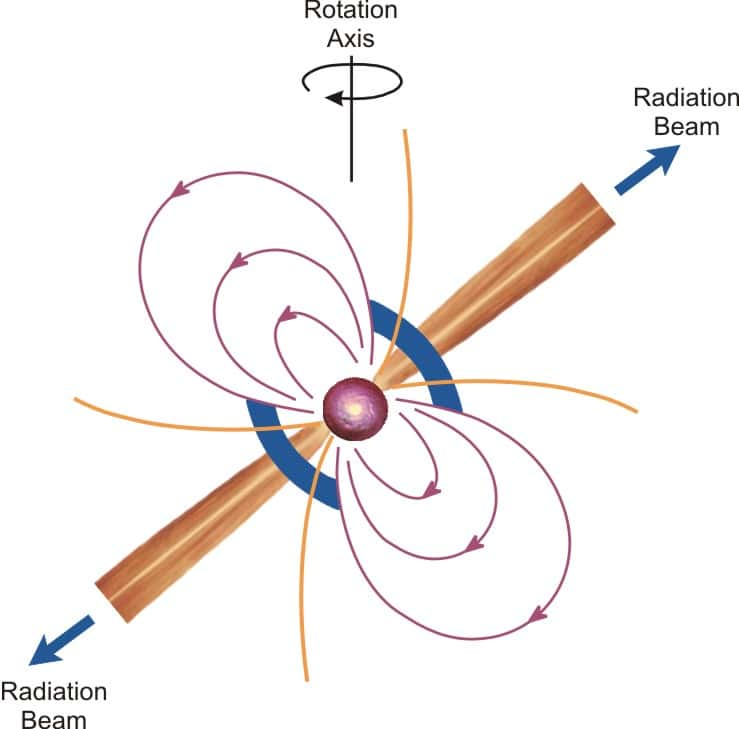
En ce qui concerne les étoiles à neutrons, le regain d'intérêt vint de la découverte en 1967 du premier "pulsarpulsar" par la Britannique Jocelyn Bell, étudiante d'Antony Hewish (qui reçut cependant seul le prix Nobel pour cette découverte). En effet, quelques jours à peine après la publication de l'observation de Bell et Hewish, l'Américain T. Gold et l'Italien F. Pacini proposèrent indépendamment d'interpréter le signal pulsant comme l'émission synchrotron produite par des particules chargées de hautes énergies se propageant le long des lignes de champ de la magnétosphèremagnétosphère d'une étoile à neutrons en rotation. Bien qu'il y eut initialement d'autres modèles, ce modèle dit du phare fut rapidement retenu et validé. La raison en est qu'après la première observation d'un pulsar, beaucoup d'astronomesastronomes tentèrent d'en trouver d'autres, et ainsi, à la fin de l'année 1968, une vingtaine déjà étaient connus. Or, le modèle du phare prédisait divers effets8 qui furent tous verifiés avant 1970. Avec l'amélioration des techniques observationnelles, on en connaît aujourd'hui plus de 2000, ce chiffre croissant sans cesse. Les étoiles à neutrons étant des objets extrêmement denses et compacts dans lesquels les noyaux atomiques sont dissous, l'espoir actuel est d'en faire des "laboratoires" pour étudier la matière à très hautes densités et énergies, et ce, en partie grâce aux ondes gravitationnellesondes gravitationnelles qu'ils émettent (voir plus loin).
Quant aux trous noirs, l'un des premiers événements/résultats-clés dans leur étude fut la découverte par le Néo-Zélandais Roy Kerr de la généralisation de la solution de Schwarzschild au cas où la masse M est en rotation avec un moment angulaire J fixé, découverte agrémentée de la démonstration que cette solution comporte elle aussi une singularité interne9. Dans la solution de Kerr, cette dernière est cependant annulaire et peut être évitée par un observateur qui entrerait dans le trou noir théorique. Ces propriétés ne sont toutefois pas pertinentes pour un véritable trou noir car l'intérieur de la solution mathématique de Kerr est instable, ce qui signifie que l'on ignore en grande partie ce qui se passe au-delà de l'horizon d'un trou noir physique en rotation, même si on a de bonnes raisons de penser que la singularité est, tout comme dans le trou noir de Schwarzschild, « un moment » plutôt qu'« un endroit ».
Peu après, la découverte de Kerr, les Britanniques Roger PenroseRoger Penrose et Stephen HawkingStephen Hawking démontrèrent de manière générale et rigoureuse que l'effondrement gravitationnel d'une étoile résulte inévitablement en l'apparition d'une singularité, une fois que son rayon est devenu plus petit que son rayon de Schwarzschild. Ainsi, le statut de cette singularité interne, dont la description échappe encore à la physique actuelle, est très différent de celui de la singularité de l'horizon : elle ne peut pas disparaître grâce à un simple changement de coordonnées et existe "réellement". Le théorèmethéorème démontré par Penrose et Hawking implique donc qu'en plus d'être irrémédiablement présente dans les équations, cette singularité est également inévitable lors de l'effondrement d'une étoile et est physique. Cette affirmation doit cependant être nuancée par le fait que leur démonstration est effectuée dans le cadre de la relativité générale. Ainsi, il est fort probable que les effets quantiques modifient cette conclusion, sans toutefois priver le "trou noir" de sa réalité physique, celle-ci dépendant avant tout de son horizon.
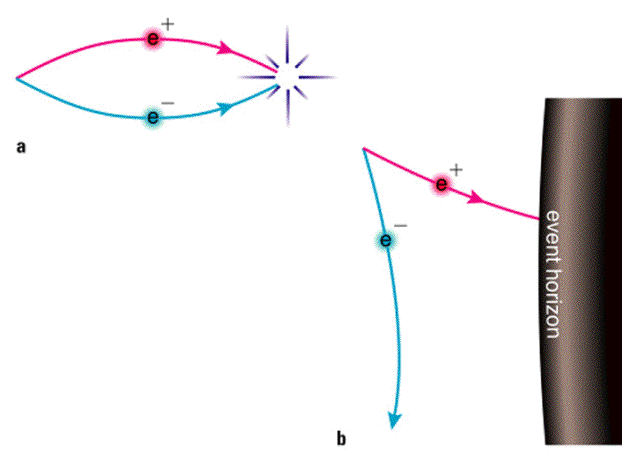
L'étape suivante dans la compréhension des trous noirs vint justement de l'étude des horizons possibles, avec les travaux du Canadien Werner Israel, de l'Australien Brandon Carter, du Britannique David Robinson et d'Hawking. Chacun d'entre eux apporta un (ou des) élément(s) de démonstration au théorème que Wheeler résuma en ces quelques mots "un trou noir n'a pas de cheveux" (à peu près à la même époque où il lança l'expression "trou noir"). Leur résultat stipule qu'indépendamment de son histoire passée, un trou noir ne peut être décrit que par trois paramètres, sa masse, sa charge électrique et son moment cinétiquemoment cinétique (encore une fois : dans le cadre de la relativité générale). Selon ce théorème, il ne reste aucune trace des autres caractéristiques décrivant l'objet avant son effondrement en trou noir (le nombre total de particules par exemple). Par ailleurs, Hawking démontra vers la même époque que la surface de l'horizon d'un trou noir ne pouvait que croître, amenant le physicien Israëlien Jacob Bekenstein à postuler que cette surface était une mesure de l'entropieentropie des trous noirs, marquant ainsi la naissance de la thermodynamiquethermodynamique des trous noirs. Cet autre pan de la physique des trous noirs fut réellement pris au sérieux par l'ensemble de la communauté lorsqu'en 1974, Hawking démontra que les trous noirs avaient effectivement une température et n'étaient donc pas complètement noirs. Utilisant la théorie quantique des champs dans le cadre des espaces-temps courbes, il venait de montrer que les fluctuations quantiques du vide à proximité de l'horizon résultent en effet en l'émission d'un "rayonnement d'Hawking". Toutefois, ce résultat est à la limite actuel entre ce qui est établi et ce qui reste spéculatif (une de ses prédictions est l'existence de mini trous noirs de durées de vie très courtes qui pourraient être formés au LHC (Large Hadron ColliderLarge Hadron Collider), ou dans d'autres collisionneurs de particules, mais sans provoquer la fin du monde comme certains l'ont craint), certains prétendant même que la démonstration d'Hawking repose sur des hypothèses encore incertaines. Ainsi, ce sujet ne sera pas plus approfondi, les observations probables de trous noirs étant un sujet bien moins spéculatif mais tout aussi intéressant.
 |
En effet, la physique des trous noirs fut également révolutionnée dans les années 1960-1970, d'un point de vue observationnel, grâce à l'apparition de la "radio-astronomie", née des importants développements techniques réalisés pendant la seconde guerre mondiale. Ainsi, commença alors l'observation du ciel non plus uniquement dans la partie visible du spectrespectre électromagnétique, mais également à d'autres longueurs d'ondeslongueurs d'ondes, notamment les ondes radio. On découvrit rapidement deux types de sources, certaines contenues dans le plan galactique, d'autres étant dispersées de manière plus isotropeisotrope, semblait-il. On pensa naturellement que les sources de cette seconde catégorie étaient extra-galactiques, ce qui fut confirmé lorsque l'amélioration des radio-télescopestélescopes permit d'associer ces sources à des galaxiesgalaxies observables. Toutefois, en 1962, la précision des mesures (cf. la précision de l'antenne utilisée en 1964 par Penzias et Wilson) était devenue suffisante pour établir avec certitude que certaines de ces sources distribuées de manière isotrope ne correspondaient à aucune galaxie connue, et qu'au contraire, on pouvait les associer à des objets qui ne se distinguaient presque pas d'étoiles. Pourtant, que des étoiles puissent émettre un rayonnement radio avec des telles intensités semblait inconcevable, mystère qui fut épaissi lorsque l'on étudia les spectres de ces "quasarquasar" (contraction de "quasi astronomical radiosource"), qui ne ressemblaient aux spectres d'aucun type d'étoiles connues et ne correspondaient pas aux raies des atomesatomes usuels. Ou tout du moins, c'est ce que l'on crut durant quelques mois, avant que l'astrophysicienastrophysicien hollandais Maarten Schmidt ne réalise que les spectres correspondaient bien à des éléments connus, mais qu'elles étaient très fortement décalées vers le rouge, ce qui signifiait que les sources étaient situées à des distances cosmologiques. Le mécanisme producteur de ces rayonnements devait donc être extrêmement puissant, et bien que les détails soient encore imparfaitement compris, l'explication actuellement reconnue vint du Britannique Donald Lynden-Bell. Celui-ci proposa en 1968 que les quasars (et autres "galaxies actives") pouvaient être la trace de l'existence au centre de ces lointaines galaxies de trous noirs supermassifstrous noirs supermassifs ayant des masses égales à plusieurs millions de fois celle du Soleil. Plus précisément, l'idée est que le rayonnement ne soit évidemment pas directement émis par ces trous noirs supermassifs, mais par de la matière située autour de ces derniers, sous forme de "disques d'accrétiondisques d'accrétion", "l'aspiration" de cette matière par le trou noir changeant l'énergie gravitationnelle de ces disques en énergie thermiqueénergie thermique émise sous forme de rayonnement.

Cliquez pour agrandir. Au-dessus, photos de quasars prises par le télescope spatial Hubble, certaines de ces photos montrant des collisions de galaxies. En dessous, illustration de l'éjection de particules de hautes énergies, en compagnie d'un schéma du "principe physique" derrière l'existence de tels jets. Source NASA.
Par ailleurs, dans les années 1960 eurent aussi lieu les premières observations astrophysiques de sources de rayonnement X. Dans un premier temps, il s'est agi de télescopes envoyés dans des ballonsballons ou fuséesfusées, jusqu'à ce qu'en 1970, soit mis sur orbite le satellite Uhuru. Grâce à celui-ci, de nombreuses sources X furent découvertes, parmi lesquelles le premier candidat trou noir stellairetrou noir stellaire, Cygnus X1, dont le spectre présentait de très brusques variations d'intensités, ce qui signifiait qu'elle était spatialement peu étendue. Rapidement, cette source X fut associée à une géante rouge HDE 226868 qui, ne pouvant être elle-même la source X, devait former avec celle-ci un système binairesystème binaire. Ce fut confirmé par les observations spectrales, qui permirent même, après quelques années, de reconstruire la dynamique du système et d'en déduire les masses de ces deux objets. En 1986, fut donc annoncé que Cygnus X1 a une masse d'environ 10 masses solaires, ce qui est bien trop important pour qu'elle soit une étoile à neutrons. Depuis cette époque, l'hypothèse selon laquelle Cygnus X1 est un trou noir a été confortée par divers autres moyens d'observation et satellites X, parmi lesquels ChandraChandra et XMM-NewtonXMM-Newton, de nombreux autres candidats trous noirs stellaires ayant également été observés. Ainsi, pour les astrophysiciens, il ne fait aujourd'hui plus l'ombre d'un doute que les trous noirs existent, même si leur observation directe est évidemment impossible par définition. Parmi les plus célèbres trous noirs, figure d'ailleurs le trou noir supermassif qui est au centre de notre Galaxie, la puissante source radio Sagittarius A*Sagittarius A*, dont on a d'abord montré qu'elle avait une masse égale à plusieurs millions de masses solaires, et plus récemment (en octobre 2002) que le volume occupé par ces masses est trop faible pour être compatible avec les explications autres que celle d'un objet de rayon inférieur à son rayon de Schwarzschild, un trou noir supermassif. Comme mentionné précédemment, il est probable que l'interférométrieinterférométrie à très longue base permette, à travers les expériences Event Horizon Observer ou GRAVITY, d'observer sous peu le voisinage de Sagittarius A*. Il existe cependant une autre observation attendue avec grande impatience et qui ne devrait pas tarder non plus, celle de leur rayonnement gravitationnel.
 |
Illustration du principe de l'émission de rayonnement X dans un système binaire dont l'un des membres est compact alors que l'autre est une étoile géanteétoile géante (système HDE 226868 / Cygnus X1 par exemple). De la matière arrachée à l'étoile s'enroule autour du trou noir et juste avant de disparaître dans celui-ci, chauffée par l'accélération gravitationnelle, elle émet ce rayonnement X. Source NASANASA. |
1 - En dehors de l'espace-temps de Minkowski, qui est bien évidemment une solution des équations d'Einstein dans le vide, c'est-à-dire "en l'absence de matière ou d'énergie pour courber l'espace-temps".
2 - Mais également autour de la Terre si on reste à des distances où l'influence du Soleil est bien plus faible que celle de la Terre.
3 - La donnée d'une "solution des équations d'Einstein" n'est rien d'autre que celle d'un tenseurtenseur énergie-impulsion décrivant la répartition de matière et celle de la métrique correspondante. Ainsi, dans le vide il s'agit uniquement de la donnée d'une métrique (mais telle que le tenseur de Ricci associé soit nul pour qu'elle soit solution des équations d'Einstein).
4 - On entend parfois dire que Landau aurait eu l'idée des étoiles à neutrons le soir même de l'annonce de la découverte du neutron, mais des études récentes montrent que la réalité serait encore plus surprenante que ce qui semble n'être qu'un mythe fondé sur de mauvais souvenirs : Landau aurait eu l'idée avant même la découverte du neutron.
5 - Il y a cependant une différence entre le cas de la Terre et celui de l'espace-temps de Schwarzschild qui est que pour décrire la Terre intégralement il faut nécessairement au moins deux cartes, alors qu'il existe des systèmes de coordonnées (=cartes) qui, si l'on néglige les coordonnées angulaires, décrivent l'espace-temps de Schwarzschild intégralement (voire même pour certains un espace-temps plus vaste dont l'espace-temps de Schwarzschild n'est qu'une partie).
6 - Le fait que la courbure devienne infinie en ce point de l'espace traduit simplement que la relativité générale échoue, tout comme la gravitation newtonienne, à décrire des objets véritablement ponctuels. Une telle description, exempte de divergences, viendra probablement d'une description quantique de la gravitation.
7 - Le physicien américain David Finkelstein est celui qui a popularisé en 1958 le système de coordonnées initialement découvert par Eddington tout en démontrant qu'il permettait également de décrire l'intérieur du trou noir de Schwarzschild.
8 - les trois principales prédictions sont :
- le temps typique de ralentissement découlant du freinage magnétique ;
- l'association entre pulsars et restes de supernovae, et l'on découvrit dès 1968 un pulsar au centre de la Nébuleuse du crabeNébuleuse du crabe, reste de la supernovareste de la supernova de 1054 observée par les Chinois, ainsi que dans Vela ;
- des périodes de rotationpériodes de rotation aussi faibles que celles du Crabe ou de Vela, respectivement 33 et 89 ms.
9 - la solution "trou noir en rotation" est différente de celle découverte par Schwarzschild à cause du caractère indélibile de la rotation, par opposition avec la quantité de mouvementquantité de mouvement. Le fait que cette dernière puisse être effacée par un changement de coordonnées adéquat illustre d'ailleurs en quoi la "masse relativiste", qui varie avec la vitesse, n'est pas un concept très utile en relativité générale : la courbure de l'espace-temps impliquée par un système massif résulte de sa masse au repos et non de sa masse relativiste.