au sommaire
La gravitation newtonienne face au principe de relativité
A - La gravitation newtonienne
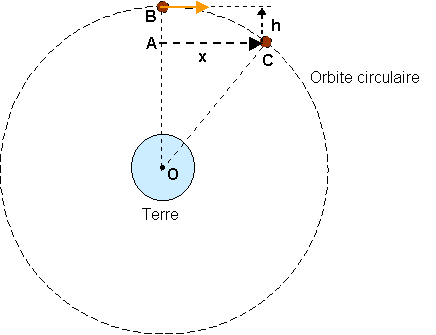
C'est avec Newton que commença réellement l'histoire de la gravitation, puisque la pesanteur et la cause potentielle du mouvement des planètes étaient auparavant considérées de manières indépendantes. Ainsi, la mécanique de Newton et sa théorie de la gravitation universelle réalisèrent l'unification des mondes sublunaire et céleste, mais bien évidemment, Newton n'eut pas, malgré son génie, une soudaine révélation, et comme il le dit lui-même, son oeuvre repose "sur les épaules des géants" qui l'avaient précédé. Il existe toutefois une légende selon laquelle il aurait eu l'idée du caractère universel de la gravitation en voyant chuter une pomme. Celle-ci lui aurait fait comprendre que la Lune tombait, à sa manière, vers la Terre, ce qui l'empêche de tomber en ligne droite étant son mouvement initial et son inertie. Selon l'interprétation de Newton, à chaque instant la Lune poursuit son chemin en ligne droite (suite à son inertie) et chute vers le centre de la Terre (à cause de la force de gravitation exercée par celle-ci), la combinaison des deux mouvements donnant lieu à une trajectoire circulaire.

Illustration de la composition instantanée du mouvement d'un satellite (la Lune par exemple) en orbite circulaire autour de la Terre. A chaque instant, la Lune poursuit sa route en ligne droite sur une longueur "x" (à cause de son inertie) et simultanément chute d'une hauteur "h" en ligne droite vers le centre de la planète (à cause de la gravitation), le mouvement résultant étant circulaire. Source R. Mauduit.
Cependant, Newton ne se contenta pas d'une explication qualitative comme celle-ci, et utilisant, entre autres choses, les travaux de Kepler (les trois lois), il réussit même à donner précisément l'expression de la force de gravitation. Rappelons toutefois que Newton élabora simultanément sa mécanique (où la notion de force est définie), sa gravitation et le formalisme mathématique pour les manipuler. Quant à sa gravitation, elle peut être décrite ainsi: étant donnés deux objets ponctuels de "masses graves" M1 et M2 séparés par une distance "r", la force qu'exerce la première masse sur la deuxième est
- attractive, dirigée le long de la droite joignant les deux masses;
- proportionnelle au produit des deux masses graves;
- inversement proportionnelle au carré de la distance entre les deux masses.
Ce qui conduit à l'écriture F = - G M1 M2 u/r²,
où G est la "constante de Newton" (qui vaut environ 6.67 × 10−11 dans les unités du système international, soit des kgkg-1 m3 s-2) et u un "vecteur unitaire" (flèche de longueur égale à 1) dirigé du premier objet vers le second.
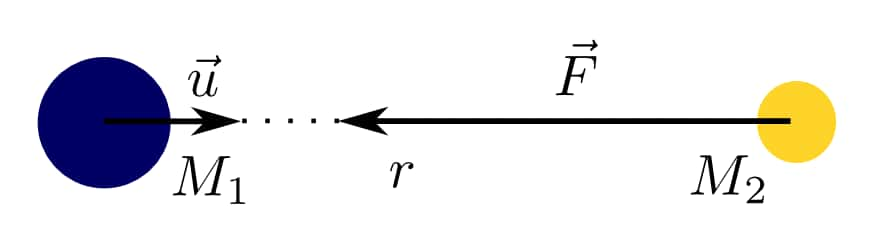
Illustration de la force de gravitation exercée selon Newton par la Terre sur la Lune.
Comme cela a déjà été expliqué, cette simple loi permit la compréhension de l'ensemble des mouvements célestes, la mécanique céleste n'étant toutefois complètement développée qu'aux XVIIIème et XIXème siècles, après les travaux du Suisse Leonhard EulerLeonhard Euler, ainsi que des Français Joseph Louis de Lagrange et Pierre-Simon LaplacePierre-Simon Laplace. Ces derniers découvrirent et appliquèrent les techniques mathématiques (calcul perturbatif, etc.) qui permettent de traiter le problème de corps non-ponctuels et/ou en nombre supérieur à deux, cas nécessaires à étudier pour aller au-delà de la description keplerienne. Cependant, un point très important a été pour le moment occulté dans la force gravitationnelleforce gravitationnelle newtonienne : la signification du terme "masse grave".
Quand Newton établit sa mécanique, il introduisit une grandeur physiquephysique nommée inertie (ou masse inerte), qui traduisait la capacité d'un corps à rester dans le même état de mouvement. Pour un matériaumatériau donné, cette "masse inerte" est proportionnelle à la "quantité de matièrematière" (autre notion introduite par Newton dans ses "Principia"), la densité (masse divisée par la quantité de matière) étant ce qui différencie deux matériaux. Mais la grandeur physique "masse inerte" n'est réellement définie que par son apparition dans la deuxième loi de Newton
F = m a.
Par ailleurs, comme Newton en était conscient, la "masse pesante" (ou grave), qui intervient dans la gravitation, est une grandeur physique qui n'a, a priori, rien à voir avec la première, puisqu'elle caractérise la faculté à attirer ou être attiré par une autre masse grave1. Toutefois, comme semblait l'indiquer la chute des corps et comme le vérifia Newton grâce à des pendules de diverses compositions, le rapport entre ces deux masses est égal à une constante "K" qui ne dépend pas de la composition. En effet, si l'on pose
g = - G M u/r²,
champ de pesanteur créé par la Terre (de masse grave M) à un endroit donné situé à une distance "r" de son centre, le principe fondamental de la dynamique newtonienne donne pour un objet en chute libre
mI a = mG g,
où l'on a introduit les masses inerte et grave de l'objet ponctuel. Cette équationéquation peut se réécrire
a = g mG/mI,
qui décrit bien le fait que l'accélération (et donc le mouvement) est la même pour tous les corps en chute libre si et seulement si K = mG/mI est une constante. En outre, en définissant la constante de Newton comme il faut, la constante "K" peut être posée égale à 1. Mais il est crucial de comprendre que cette égalité n'a, a priori, aucune raison d'être. Ainsi, il est nécessaire de la tester, ce qui fut fait, avec une grande précision au début du XXème siècle, par le Hongrois Loránd Eötvös grâce à un "pendule de torsiontorsion".
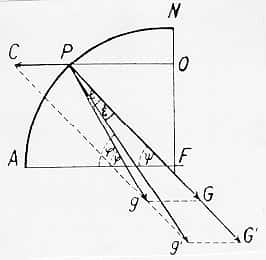 | |
| Illustration du principe de l'expérience d'Eötvös. Deux objets de compositions différentes mais de même masse inertielle situés au point P devraient subir la même force centrifugeforce centrifuge (due à la rotation de la Terre), avec cependant des forces gravitationnelles différentes, si les masses graves ne sont pas égales. Ceci devrait résulter par l'existence de deux champs de pesanteur effectifs différents (g et g' sur le dessin), impliquant une asymétrie du système formé des deux masses et donc un effet mesurable lorsque celles-ci sont interverties. Cependant, en accord avec le principe d'équivalence des masses grave et inerte, aucun effet ne fut détecté. Source P. Király. | |
L'idée originale d'Eötvös fut d'utiliser un système formé de deux masses de compositions différentes et de comparer deux configurations d'équilibre statique où ces masses avaient été inversées. Grâce à sa procédure, il obtint deux équilibres décrits par deux équations très semblables, la seule différence entre celles-ci étant la permutation des rapports "K" de chacun des corps. Le grand progrès réalisé ainsi vis-à-vis des expériences précédentes (la chute libre par exemple) est que l'on mesure de potentielles petites déviations par rapport à deux non-mouvements (= grandeur nulle), et non plus des déviations entre deux mouvements (= grande composante), ce qui permet une bien meilleure précision.
Eötvös vérifia que le rapport K était le même pour tous les matériaux avec une précision de l'ordre d'une partie pour 100 millions (1/108), son expérience étant améliorée jusqu'à une précision d'une partie pour 1000 milliards (1/1012), par le physicienphysicien américain Robert Henri Dicke, qui, dans les années 1960, réussit à refroidir suffisamment le système pour diminuer les "fluctuations thermiques" (agitements aléatoires des moléculesmolécules liés à la chaleurchaleur). Cependant, cette égalité restait, dans la théorie de Newton, une sorte de principe mystérieux, et c'est seulement avec EinsteinEinstein qu'elle acquit un caractère d'évidence grâce, encore une fois, à un changement de point de vue que ce dernier proposa. Mais même si cette égalité entre masses grave et inerte fut cruciale pour l'émergenceémergence de la relativité généralerelativité générale, celle-ci résulta avant tout des incompatibilités entre la gravitation newtonienne et le principe de relativité einsteinien.
B - La gravitation face à la relativité restreinte
Bien évidemment, la théorie newtonienne de la gravitation, née en même temps que la mécanique newtoniennemécanique newtonienne, respecte le principe de relativité galiléen. Néanmoins, comme cela a déjà été signalé, l'utilisation du concept de force instantanée agissant à distance la rend incompatible avec le principe de relativité revisité par Einstein. Ce dernier implique en effet le renoncement à la notion de simultanéité absolue et l'impossibilité d'avoir un transfert d'information à une vitessevitesse supérieure à "c", alors qu'une force instantanée à distance correspond justement à une vitesse infinie pour le transfert d'information. Techniquement, ces problèmes se traduisent par l'impossibilité d'écrire la théorie de Newton sous une forme qui ne dépende pas de l'observateur lorentzien choisi : on dit que les équations de Newton ne peuvent pas être mises sous une forme covariante vis-à-vis des transformations de Lorentz. Notons toutefois que la formulation de la gravitation newtonienne employée pour cette quête d'une gravitation covariante n'est pas exactement celle présentée plus haut, mais celle introduite en 1777 par Lagrange, qui a montré l'utilité du concept de potentiel gravitationnel, notion qui se rapproche beaucoup de celle de champ introduite plus tard en électromagnétismeélectromagnétisme par Faraday et Maxwell.
D'un point de vue moderne, le potentiel gravitationnel newtonien est un champ scalaire, c'est-à-dire un objet mathématique défini dans tout l'espace et qui associe à chaque point de l'espace un nombre. Si l'on trace des courbes joignant tous les points associés à la même valeur du potentiel, on obtient les courbes isopotentielles (en pointillés sur la figure suivante). Un exemple mathématiquement similaire est celui des courbes isobaresisobares utilisées en météorologiemétéorologie qui ne sont rien d'autre que les courbes le long desquelles la pressionpression (autre exemple de champ scalaire) garde une valeur constante. L'un des intérêts de ces lignes isopotentielles est qu'elles permettent de connaître, en un point donné, la force de gravitation qu'exerce le corps source du potentiel sur un objet situé en ce point, sans même savoir où se situe la source du champ considéré : c'est une description purement locale. Pour obtenir la "flèche" (= vecteur) qui représente cette force, il suffit de tracer une perpendiculaire à l'isopotentielle passant par le point, et de la diriger vers l'isopotentielle de valeur inférieure (on trouve ainsi la direction et le sens). L'intensité de la force (= longueur de la flèche) est quant à elle d'autant plus grande que la répartition des lignes isopotentielles est dense au point considéré (si la valeur du champ est constante dans tout l'espace, il n'y a donc pas de force, puisqu'il n'existe pas d'isopotentielle de valeur inférieure). Sur la figure suivante, qui représente le champ gravitationnel créé par l'objet central, les forces sont représentées par des flèches d'autant plus longues (= force intense) qu'elles sont situées près du corps (= là où l'on observe plus de lignes sur une même surface). Si l'on souhaitait poursuivre l'analogieanalogie météorologique entamée plus haut, on pourrait mentionner la force résultant des inhomogénéités de la pression. Pour que cela soit utile et relié aux cartes habituellement présentées, par exemple les ventsvents, il faudrait toutefois également prendre en compte la rotation de la Terre, les effets liés à la température et diverses autres complications. Ainsi, on se contentera de signaler que la force exercée par la pression est elle aussi d'autant plus grande que ses variations sont rapides, mais qu'en pratique les déplacements d'airair ne sont pas uniquement liés à cela.
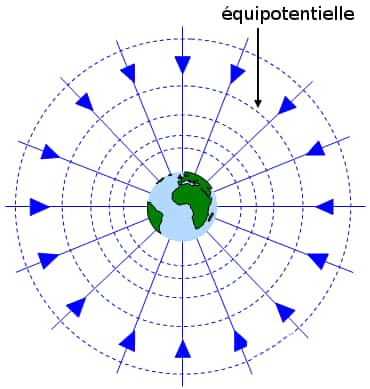
Illustration du concept de potentiel gravitationnel introduit par Lagrange. Sur cette figure, apparaissent des courbes isopotentielles, qui sont des sphères dans le cas d'une source à symétrie sphérique, ainsi que quelques flèches représentant la valeur de la force de gravitation en certains points. Ces forces étant orthogonales aux isopotentielles, elles sont toutes radiales et dirigées vers le centre de la source. Source : http://www.schoolphysics.co.uk/
Se reposant sur le concept de potentiel gravitationnel, Poincaré fit encore une fois preuve d'initiative et d'originalité, puisqu'il se pencha sur la recherche d'une théorie de la gravitation qui soit invariante sous les transformations de Lorentz avant même 1905, alors qu'Einstein ne se pencha sur la question que vers 1907. Cependant, même s'il eut l'intuition que la vitesse de propagation de la gravitation était probablement égale à "c" et qu'il existait peut-être des "ondes gravifiques"2, Poincaré fut à nouveau trop conservateur dans ses points de vue, et il n'aboutit pas, ne se décidant pas à traiter la gravitation différemment de l'électromagnétisme (comme le fit finalement Einstein). Mais à sa décharge, il convient de signaler que nombreux sont ceux qui échouèrent également face à ce problème, celui-ci n'étant réellement résolu qu'en 1915 par Einstein.
Pour trouver une théorie relativiste de la gravitation, le problème était pourtant clair : il s'agissait "tout simplement" de passer de l'équation schématique newtonienne
Variation du champ de gravitation = densité de masse,
à l'équation relativiste
Variation relativiste du champ relativiste de gravitation = densité relativiste de masse-énergie,
dans laquelle le "champ relativiste de gravitation" et la "densité relativiste de masse-énergieénergie" étaient toutefois des variables à identifier, alors que la "variation relativiste" était également un nouvel opérateur mathématique à découvrir.
Cependant, la "densité relativiste de masse-énergie" n'était pas si difficile que ça à identifier. En effet, un objet mathématique généralisant la densité de masse de manière relativiste, le tenseurtenseur énergie-impulsion3, avait été rapidement mis en évidence dans le contexte de la relativité restreinterelativité restreinte. Ce tenseur apparaît naturellement, dans le cadre de la relativité, suite à l'apparition de deux (quadri)vecteurs précédemment mentionnés : celui rassemblant l'énergie d'une particule et son impulsion (le quadrivecteur impulsion-énergie), ainsi que celui rassemblant la densité de charge électrique et son flux (=vecteur tridimensionnel associé à "l'écoulement" de cette charge). Plus précisément, l'existence du premier quadrivecteur montre que l'on ne peut plus séparer énergie et impulsion (et implique l'équivalence entre masse et énergie), alors que le deuxième montre que toute grandeur physique distribuée de manière continue (comme la densité de charge) doit être associée au vecteur tridimensionnel décrivant son transport pour former un quadrivecteur. Ainsi, si l'on considère la quantité physique décrite par le quadrivecteur énergie-impulsion, on comprend intuitivement très bien que si l'on souhaite s'intéresser à une distribution continue de cette grandeur (généralisation de la notion de distribution continue de masse), alors sa description complète passe par un "flux relativiste" pour chacune de ses composantes, soit 4 x 4 = 16 nombres formant le tenseur énergie-impulsion4.
Parmi les diverses tentatives qui furent réalisées, il est intéressant de mentionner la théorie du physicien finlandais Gunnar Nordström, dont le nom est avant tout resté dans l'histoire de la physique pour sa découverte, avec l'Allemand Hans Reissner, d'une solution des équations de la relativité générale qui décrit un trou noirtrou noir possédant une charge électrique non-nulle. Essayant comme Poincaré5 le cas le plus simple possible, Nordström proposa en 1912 une théorie de la gravitation relativiste dans laquelle le pendant relativiste du potentiel gravitationnel newtonien était un champ scalaire vérifiant une équation covariante sous les transformations de Lorentz. Plus précisément, l'idée était qu'il existe une équation "aux dérivées partielles" covariantes reliant ce potentiel gravitationnel et une autre quantité "scalaire" formée à partir du tenseur énergie-impulsion. Mais c'était là l'une des erreurs stratégiques de Nordström que d'essayer de continuer à décrire la gravitation par un champ scalaire. En effet, le succès d'Einstein, quelques années plus tard, repose entre autres choses sur une description de la gravitation dans laquelle le champ gravitationnel est lui-aussi un tenseur, la source de cette gravitation étant le tenseur énergie-impulsion. Cependant Einstein ne fut évidemment pas le seul à avoir abordé le problème de cette façon, et s'il réussit c'est uniquement grâce à une autre intuition géniale qu'il avait eue : sa relecture de l'universalité de la chute libre.
1 en toute rigueur, il conviendrait également de différencier la "masse grave active" (qui crée la force) de la "masse grave passive" (qui subit la force). Mais cette complication sera ignorée ici puisque les expériences indiquent, avec une très grande précision, l'égalité entre ces deux masses.
2 on parle aujourd'hui plutôt "d'ondes gravitationnellesondes gravitationnelles", voir plus loin.
3 cf., si besoin était, la brève explication sur la notion de "tenseur" présentée lors de la description du tenseur antisymétrique, formé par les champs électriquechamps électrique et magnétique, dans la page sur les applicationsapplications de la relativité restreinte.
4 pour qui serait à l'aise avec les notions tensorielles et la mécanique des milieux continus mais pas la relativité, on peut ajouter que le tenseur énergie-impulsion est également la généralisation relativiste du tenseur des contraintes visqueuses. Par ailleurs, il faut noter que ce "tenseur" est en fait un "champ tensoriel symétrique" : à chaque point de l'espace-tempsespace-temps est associée une valeur de ce tenseur dont seules 10 composantes sont indépendantes.
5 il faut cependant signaler que les travaux de Nordström suivirent les premières publications d'Einstein sur la gravitation relativiste alors que ceux de Poincaré les précédèrent.