au sommaire
En résumé : ce qu'il faut retenir sur le corps noir
Le dossier précédent semblera certainement difficile à lire à beaucoup, et avec juste raison, car le sujet est vaste et fait intervenir de nombreux concepts physiques et mathématiques non triviaux.
Même si l'on peut apprendre beaucoup de choses en première lecture, en passant sur les parties les plus délicates, il est certain que ce dossier demande du temps et du travail pour explorer son contenu. Pour le lecteur pressé, ou ayant besoin de trouver rapidement quelques uns des liens donnés tout au long du texte, on a donc ajouté un résumé des choses importantes à retenir de ce voyage dans l'histoire et les arcanes du monde fascinant de la physique du XX ième siècle.
La théorie du corps noir est l'un des plus vieux problèmes de la physique théorique et il est à l'origine de la physique quantique. On retrouve la théorie du corps noir aussi bien lorsque l'on veut comprendre ce que sont fondamentalement la lumière et la matière que lorsque l'on étudie les étoilesétoiles, les trous noirstrous noirs et même la cosmologiecosmologie.
Le problème de la théorie du corps noir prend racine dans des considérations très concrètes : pourquoi et comment un corps émet-il de la lumière lorsqu'on le chauffe ?
Ces questions, les physiciensphysiciens du début du XIX ième siècle se les étaient posés dans le cadre de la naissance de la thermodynamiquethermodynamique. On était alors en pleine révolution industrielle, le problème de savoir comment construire des machines à vapeur puissantes et performantes était à l'esprit de beaucoup d'ingénieurs.
Quelles étaient les lois qui permettaient de transformer la chaleurchaleur en travail mécanique ? Pouvait-on brûler moins de charboncharbon en produisant plus de travail ? Comment la chaleur pouvait-elle produire telles réactions chimiquesréactions chimiques intéressantes pour l'industrie ?
A côté de cela, les théoriciens cherchaient aussi une image unitaire du monde. Pouvait-on considérer la lumière, la chaleur, la gravitationgravitation, l'électricité et le magnétismemagnétisme comme différentes faces d'une même série de lois ?
Comprendre et quantifier les caractéristiques de la lumière émise par un corps chauffé semblait donc à l'intersection de beaucoup de problèmes importants de la physique et de la technologie. On savait bien que la couleurcouleur d'un corps changeait, passant du rouge au blanc au fur et à mesure que sa température augmentait. On savait aussi qu'il émettait alors d'autant plus de lumière, mais, quelles étaient les formules numériquesnumériques précises pour rendre compte de ces phénomènes ?
C'est Kirchhoff qui fut le premier à trouver ces lois. Il découvrit qu'il existait une série de lois universelles valables pour tous les corps, quels que soient leurs compositions et leur états, gazgaz ou solidesolide. Ces lois étaient plus faciles à mettre en évidence si l'on considérait la lumière émise par un corps noir.
Cela semble surprenant et même absurde, un corps noir n’émet pas de lumière par définition non ?
Pas avec la définition qu'en donnent les physiciens. Un corps soumis à de la lumière en absorbe une partie, en réémet une autre, et ces quantités peuvent être définies par des coefficients. Un corps noir n'est pas un corps qui ne fait qu'absorber à toutes les longueurs d'ondeslongueurs d'ondes, ce qui est une définition intuitive de base, il peut aussi réémettre à toutes les longueurs d'ondes. La définition du corps «noir» par un physicien n'est donc pas celle d'un corps absolument pas lumineux, mais celle d'un corps parfaitement absorbant.
Une autre caractéristique importante d'un corps noir en physique est reliée étroitement à la notion d'équilibre thermique. Deux corps sont en équilibre thermique/thermodynamique lorsqu'ils sont à la même température, comme c'est le cas au bout d'un moment lorsqu'un bloc de métalmétal chaud est plongé dans de l'eau.
On peut réaliser un rayonnement de corps noir en chauffant uniformément à la température T les parois d'une enceinte de composition quelconque et en faisant un petit trou dans celle-ci pour laisser passer le rayonnement résultant.
Pour comprendre la nature du rayonnement produit il faut avoir à l'esprit que si l'on considère un corps quelconque on peut introduire les quantités et
, respectivement le pouvoir absorbant et le pouvoir émissif d'un corps à la fréquencefréquence
.
La thermodynamique implique alors l'existence d'une fonction universelle , caractérisant la quantité d'énergieénergie émise par unité de temps à l'équilibre thermique et ne dépendant que de la température et de la fréquence de ce rayonnement. C'est l'une des lois découvertes par Kirchhoff
On doit nécessairement avoir aussi la relation suivante qui est la seconde loi découverte par Kirchhoff (Attention à ne pas confondre ces lois avec celles qu'il a découverte en spectroscopie et en théorie des circuits électriques).
Si l'on suit la définition de Kirchhoff d'un corps noir, un corps parfaitement absorbant, alors vaut 1. Le pouvoir émissif de ce corps est donné par la fonction
mais comme
vaut 1, cette fonction s'identifie avec la fonction
.
On aura donc :
Quel que soit le corps émettant de la lumière, à l'équilibre thermodynamique, la formule donnant la répartition de l'énergie rayonnée par bande de fréquence sera celle d'un corps noir !
Bien sûr, les corps ne sont jamais exactement des corps noirs, et surtout, ils ne sont pas toujours en équilibre thermodynamique avec un rayonnement. Il n'en restera pas moins que l'on aura toujours, à l'équilibre thermodynamique, une loi reliant absorptionabsorption et émissionémission de ce corps à une fréquence donnée avec ce qu'on appellera désormais la loi du corps noir.
Les physiciens Wien, Stefan et Boltzmann, en l'absence d'une forme précise pour la fonction (Black body voulant dire corps noir en anglais) vont tout de même réussir à prouver qu'elle doit nécessairement conduire à deux autres relations fort importantes : la loi de déplacement de Wien et la loi de Stefan-Boltzmann
Cette dernière donne la quantité d'énergie qu'émet, par unité de surface et par unité de temps, un corps noir à la température T
Pour une surface A elle implique donc une luminositéluminosité totale L donnée par:
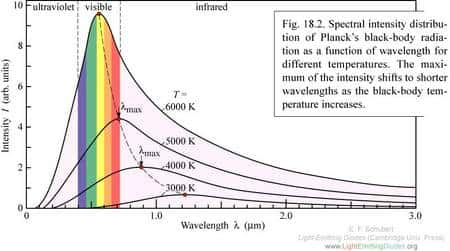
Enfin, si l'on exprime la loi du corps noir en fonction de la longueur d'onde du rayonnement, et que l'on cherche le maximum de l'émission à une température donnée en kelvinskelvins, on démontre que celui-ci se trouve à une longueur d'onde lambda vérifiant ce qu'on appelle la loi du déplacement de Wien.
En général, dans la bande visible, celle-ci correspond à une couleur, ce qui permet d'estimer la température d'un corps chauffé rayonnant juste à partir de celle-ci.
Sur la figure ci-dessous, on a représenté la courbe expérimentale de la distribution spectrale du corps noir à différentes températures mais en fonction, non plus de la fréquence , mais de la longueur d'onde. On voit clairement que le maximum de l'intensité lumineuse émise varie avec la température.

Ces lois sont importantes en astrophysiqueastrophysique et en physique car, de la couleur d'un corps chauffé on peut déduire sa température.
Si, dans le cas des étoiles par exemple, on connaît la luminosité L en plus de la température déterminée par la loi de Wien, on peut remonter à la surface A et donc au rayon de l'étoile. Il faut bien sûr qu'une étoile puisse être considérée en première approximation comme un corps noir : c'est bien le cas et, comme indiqué précédemment, cela n'est pas contradictoire avec la définition du corps noir donnée par la physique.
Pendant longtemps, les volcanologuesvolcanologues se sont servis de la couleur des laveslaves pour estimer leur température: une applicationapplication directe de la loi de Wien. On parle d'ailleurs dans ce cas, comme pour la théorie des étoiles, de température de couleurtempérature de couleur. La température effective sera celle estimée avec la loi de Stefan-Boltzmann.

Fontaine de lave à Krafla en Islande (Crédit : ereiter.free.fr).
Le corps noir et la naissance de la mécanique quantique
Il a fallu attendre le 19 octobre 1900 pour que Max PlanckMax Planck rende public le résultat de ses dernières recherches dans un article désormais célèbre: "Sur la théorie de la loi de la distribution d'énergie du spectrespectre normal". Dans celui-ci, il donnait enfin la formule exacte pour le rayonnement d'un corps noir.
La formule de Planck s'écrivait alors sous la forme suivante :
Ce qui, si l'on préfère une distribution en longueur d'onde, plus adaptée aux mesures en spectroscopie, donnera :
C'était le début d'une révolution, car Planck, pour dériver sa formule, était contraint d'admettre que les échanges d'énergies entre la matière et le rayonnement ne pouvaient se faire que par quanta d'énergie discrets.
Une révolution théorique et technologique était en marche car ce n'est ni plus ni moins que la date de naissance de la physique quantique, laquelle est à l'origine, par exemple, de toute notre électronique moderne avec les laserslasers et les semi-conducteurssemi-conducteurs.

Par l'intermédiaire des travaux d'Einstein de 1917, le laser est une application de la théorie quantique.
Toutefois, refusant de remettre en cause fondamentalement la physique classique, Planck ne réalisa pas tout de suite les conséquences de sa découverte.
EinsteinEinstein fut le premier à comprendre qu'il ne s'agissait pas seulement de restriction à la façon dont l'énergie pouvait être échangée entre les systèmes physiques, mais bien que l'énergie elle-même se présentait toujours sous forme granulairegranulaire conformément à la formule de Planck-Einstein reliant un quanta d'énergie E à une fréquence
(Dans le cas de la lumière, ces grains furent plus tard appelés des photonsphotons par le chimiste et physicien américain Gilbert Lewis).
Il fut bientôt suivi par Bohr en 1913, l'année de l'introduction de son modèle atomique basé sur l'hypothèse des quanta de Planck et les années 1925-1927 virent peu à peu la constitution d'une nouvelle science : la mécanique quantiquemécanique quantique.
Pour tous les physiciens de cette période, notamment Einstein, Heisenberg, Born, Jordan, Bose, Dirac, l'analyse de la formule de Planck sous tous ses aspects allait se révéler très fructueuse pour l'exploration du monde quantique.
La clé du monde atomique ouvrit alors d'autres portesportes: celles des étoiles et de la cosmologie.
Il devenait possible de comprendre en détails la lumière émise par des objets astrophysiques fort variés en compositions chimiques, températures et champs magnétiqueschamps magnétiques. Là encore, les formules de Kirchhoff, Wien, Stefan-Boltzmann et Planck furent employées en plus des équationséquations générales de la mécanique quantique. L'application la plus spectaculaire est sans doute celle de la cosmologie elle-même.
Le corps noir et la théorie du Big Bang
Si l'on prend en effet au sérieux les équations de la relativité généralerelativité générale d'Einstein, on trouve, comme l'expérience le vérifie, que l'UniversUnivers peut très difficilement rester dans un état statique : il doit être en expansion ou en contraction et cela doit s'accompagner d'un décalage spectral d'autant plus prononcé que la lumière émise par les astresastres nous provient de régions éloignées de notre GalaxieGalaxie.
L'Univers observable pouvait donc être dans un état plus dense et plus chaud il y a des milliards d'années. En effet, comprimer un gaz revient à le chauffer et lorsque la matière présente dans l'Univers observable, essentiellement sous forme d'hydrogènehydrogène et d'héliumhélium, pensait-on alors, était réduite à un volumevolume beaucoup plus petit qu'actuellement, elle devait être chaude et donc rayonner.
On peut montrer qu'un équilibre thermique devait alors régner, ce qui veut dire que l'intensité lumineuse de la lumière, à cette époque reculée, devait suivre la loi de Planck. En outre, des vestiges de celle-ci, des photons fossilesfossiles, devaient persister aujourd'hui.
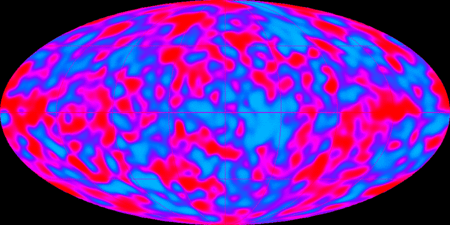
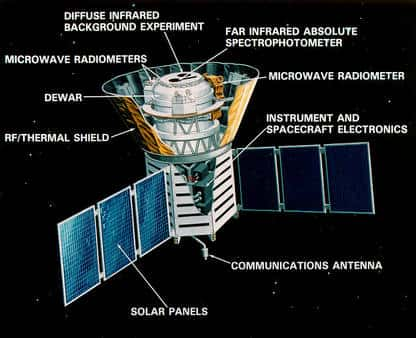
Ce rayonnement de corps noir fut effectivement découvert en 1965 par Penzias et Wilson et sa température est d'environ 2, 7 K. Ce fut la première preuve de la théorie du Big BangBig Bang et l'étude des détails fins de ce rayonnement millimétrique, le CMB ou Cosmic Microwave Background, a fait l'objet de toutes les attentions avec les satellites COBE, WMAPWMAP et bientôt PLANCK. Deux prix Nobel sont venus récompenser les auteurs de ces travaux, Penzias et Wilson en 1979, et Smoot et Mather en 2006.
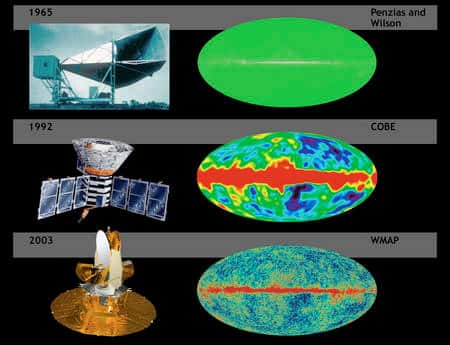
Le gain en précision pour les images du rayonnement fossile au cours du temps (Crédit : NASA).
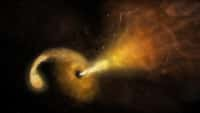
Stimulés par le succès des prédictions de la relativité générale, les astrophysiciensastrophysiciens ne tardèrent pas à étudier intensivement une autre de ses prédictions : les trous noirs.
Là aussi, de façon très étonnante, la loi du corps noir de Planck intervient.
Wheeler, Bekenstein, Hawking et le corps noir
Le grand physicien John Wheeler, qui avait été l'auteur de la première théorie de la fission nucléairefission nucléaire avec Niels BohrNiels Bohr, le directeur de thèse de Feynman et l'un des créateurs de la bombe H américaine, après avoir été un ardent promoteur de l'étude des étoiles totalement effondrées qu'il avait fini par baptiser "trous noirs", s'était interrogé sur les principes de la thermodynamique en cosmologie.
Comme une étoile s'effondrant pour former un trou noir ressemble beaucoup à un Univers en expansion, mais avec le sens du temps inversé (l'expansion se changeant en contraction), cela revenait à étudier si oui ou non un trou noir respectait les lois de la thermodynamique.
En particulier, avec son étudiant Jacob Bekenstein, il cherchait à savoir si le second principe de la thermodynamiquesecond principe de la thermodynamique, introduisant une grandeur appelée entropieentropie, pouvait s'appliquer dans des situations où le champ de gravitation était extrêmement fort, comme au cœur des trous noirs et lors du Big Bang.
Bekenstein montra que oui...si l'on associait l'entropie S d'un trou noir à sa surface A.
Stephen HawkingStephen Hawking ne fut pas convaincu. Et pourtant, il avait lui-même démontré que la surface d'un trou noir augmentait nécessairement au cours du temps d'après les équations classiques de la relativité générale, tout comme devait le faire l'entropie d'un système physique isolé. Ce résultat avait été baptisé le théorèmethéorème de la croissance des aires.
Pour lui, l'idée de Bekenstein était tout simplement absurde car alors, possédant une entropie, un trou noir devait aussi avoir une température et rayonner comme un corps noir. Or, même si un trou noir est parfaitement absorbant, il ne devait rien émettre à cause de sa définition même: un région de l'espace-tempsespace-temps séparée du reste de l'Univers par une sorte de soupape ne fonctionnant que dans un seul sens : son horizon.
Regardons tout cela d'un peu plus près
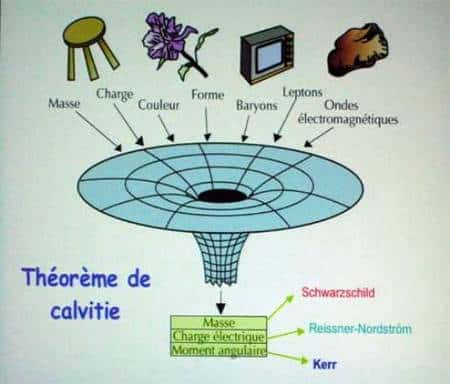
D'après Hawking donc, aucun processus classique ne peut dissocier un trou noir en deux, car la somme des aires des deux trous noirs serait alors inférieure au trou noir initial. Inversement, la fusionfusion de deux trous noirs doit donner un nouveau trou noir dont l'aire est supérieure à la somme des deux aires précédentes. Lorsqu'on connaît la relation entre l'aire A d'un trou noir et sa massemasse M (on a posé G=c=1):
il est facile de s'en convaincre, il suffit d'élever la somme des masses des trous noirs au carré.
Cependant, lors d'une école des Houches sur les trous noirs, Hawking, en collaboration avec Bardeen et Carter, avait démontré la relation suivante valable pour un trou noir en rotation et chargé:
Elle reliait les variations de la masse M d'un trou noir aux variations de la surface de son horizon A, de son moment cinétiquemoment cinétique J et enfin de sa charge Q. L'analogieanalogie avec le premier principe de la thermodynamiquepremier principe de la thermodynamique exprimé par l'équation suivante saute aux yeuxyeux:
Le terme de gauche étant celui de l'énergie totale E d'un système thermodynamique, il s'identifiera avec la masse du trou noir.
Le premier terme de droite étant celui de l'échange de travail, lorsqu'on comprime un volume V de gaz avec une pressionpression P, il correspondra aux deux derniers termes de la relation précédente. Enfin, il semble naturel, pour aller jusqu'au bout de la logique de la connexion établie, d'interpréter la surface A du trou noir comme une mesure de son entropie S, ce qui fixe aussitôt une notion de température pour le trou noir.
Cela l'est d'autant plus que le théorème de croissance de l'aire de Hawking, comme mentionné précédemment, exprime bien justement le second principe de la thermodynamique, avec sa loi de la croissance de l'entropie.
En employant une description quantique de la matière en interaction avec un trou noir, Hawking fut particulièrement surpris de découvrir que ceux-ci ne l'étaient pas vraiment. Sous l'action de forces de maréeforces de marée séparant des paires de particules/antiparticulesantiparticules juste à l'horizon d'un trou noir, un rayonnement était produit dont le spectre était précisément celui d'un corps noir! Les trous noirs possédaient bien une température et une entropie mesurée par leur surface
Hawking pouvait maintenant donner une formulation exacte de la relation que Bekenstein avait conjecturée pour l'entropie d'un trou noir. Il s'agit de la formule suivante faisant intervenir les constantes les plus importante de la physique, la vitesse de la lumièrevitesse de la lumière c, la constante de la gravitationconstante de la gravitation G et enfin celles de Boltzmann kb et de Planck .
De façon intéressante, on peut faire apparaître le carré de la longueur de Plancklongueur de Planck, lp , en dénominateur de l'aire du trou noir A. Numériquement, l'entropie d'un trou noir de masse M est donnée par la formule suivante où la masse du SoleilSoleil apparaît au dénominateur dans sa notation standard.
La luminosité totale d'un trou noir de température T et possédant une surface d'aire A va bien sûr être donnée par la loi de Stefan-Boltzmann:
Avec comme valeur de la constante de Stefan
Sa température, quant à elle sera donnée par:
où l'on voit qu'un trou noir de masse solaire est particulièrement froid si on le compare à la température du rayonnement fossilerayonnement fossile.
Un trou noir de la masse de la Terre ne rayonnerait que comme un corps noir à une température de 0,02 K environ.
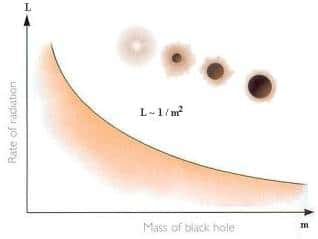
Plus un trou noir est léger plus sa température augmente et donc sa luminosité d'après la loi de Stefan-Boltzmann.
Enfin, plus un trou noir est petit moins il met de temps pour s'évaporer. Ramené à la masse de Planck Mp et au temps de Plancktemps de Planck tp de 10-44 s, le temps de vie d'un trou noir de masse M est donné par la formule suivante:
Un trou noir de la masse du Soleil mettrait ainsi environ 1067 ans pour s'évaporer. Par contre, un trou noir de 961 kgkg aurait un rayon de Schwarzschildrayon de Schwarzschild de seulement 2,85 10-24 m, serait aussi lumineux que le Soleil et aurait un temps de vie assez court. Malheureusement, jusqu'à présent, aucun mini trou noir primordial d'une masse de 1014 g et moins, susceptible de s'évaporer actuellement en émettant un rayonnement intense détectable, n'a été observé.

Représentation d'artiste d'un mini trou noir s'évaporant en émettant une gerbe de particules (Crédit : Aurore Simmonet).
On pourra s'amuser à calculer plusieurs de ces nombres grâce au programme présent sur ce site.
Posons pour simplifier les équations donnant la température et l'entropie d'un trou noir posons:
Alors, la température et l'entropie d'un trou noir pourront s'écrire sous les formes suivantes:
Un problème encore ouvert pour la physique du XXIième siècle
Les découvertes de Jacob Bekenstein et Stephen Hawking se sont révélées plus profondes et plus problématiques que prévu, au fur et à mesure que les années passaient.
D'abord, si l'on peut associer une entropie à un trou noir, comme l'entropie est aussi une mesure du désordre d'un système ou encore de l'information manquante sur ce système pour un observateur, tout se passe comme si l'information caractérisant un objet quelconque tombant dans un trou noir était enregistrée d'une façon ou d'une autre par son horizon.
En reprenant les analyses de Bekenstein, le prix Nobel de physique Gérard 't Hooft a montré que si l'on divise la surface d'un trou noir en carrés dont la longueur des côtés est donnée par la longueur de Planck, alors chaque petite plaquetteplaquette possédant une surface dite de Planck-Wheeler (10-70 m2 environ) peut stocker un bit d'information sous forme de 0 ou de 1.
Tout se passe donc comme si l'information perdue pour un observateur extérieur, et portée initialement par la structure en 3D des objets traversant l'horizon du trou noir, était maintenant codée sur une surface en 2D : exactement comme pour un hologrammehologramme !
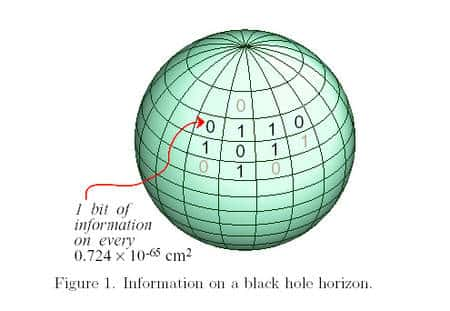
(Crédit : Gerard 't Hooft).
Si toutes ces analyses devaient être confirmées expérimentalement, alors cela conduirait à revoir de nombreuses notions sur la structure des lois de l'Univers. Les lois de la mécanique quantique et même les notions d'espace et de temps de la relativité générale pourraient n'être que des propriétés émergentes et non fondamentales. Comme 't Hooft et d'autres l'ont suggéré, la véritable nature du monde pourrait être mieux comprise si on le considérait sous l'angle de la théorie de l'information et de la théorie des automates cellulairesautomates cellulaires. Les notions de mouvementmouvement et d'énergie cesseraient alors d'être fondamentales en physique.
Toujours dans cette perspective, un problème grave se pose assez rapidement.
Comme Stephen Hawking a été le premier à le découvrir, le rayonnement d'un trou noir reste celui d'un corps noir jusqu'à ce qu'il atteigne environ la longueur de Planck. Les lois de la mécanique quantique exigent donc que le rayonnement émis soit aussi chaotique et désordonné que possible. Mais alors presque toute l'information stockée par une masse pouvant représenter des milliards de masses solaires semble irrémédiablement détruite, car il ne reste plus assez d'énergie sous forme de masse dans l'état final du trou noir pour que des processus de gravitation quantique inconnus codent l'information initiale dans les dernières phases de l'évaporation du trou noir.
Cette non-conservation de l'information entre en contradiction avec ces mêmes lois de la mécanique quantique qui imposent sa conservation : on est confronté à ce qu'on appelle le paradoxe de l'information pour les trous noirs.
Pour Gerard 't Hooft, Léonard Susskind et d'autres physiciens comme John Preskill, cela ne peut vouloir dire qu'une seule chose : le rayonnement des trous noirs n'est pas exactement celui d'un corps noir et les lois de la mécanique quantique ne doivent pas être modifiées.
Pour Stephen Hawking, au contraire, les conclusions de ses calculs, qui ne font pas intervenir de la gravitation quantique, persisteront même quand on sera allé au-delà des approximations faites jusqu'ici dans la dérivation du comportement des trous noirs. Un célèbre pari en a résulté entre lui, Kip Thorne et John Preskill, ce dernier défendant la thèse de la conservation de l'information lors de l'évaporation d'un trou noir.

De gauche à droite John Preskill, Kip Thorne et Stephen Hawking lors du pari sur le paradoxe de l'information. Hawking ne pouvant signer les termes du pari, on prend une empreinte de son pouce (Crédit : John Preskill).
Au milieu des années 90, en utilisant des résultats de la théorie des cordes, la façon dont l'information pouvait être stockée dans des trous noirs, puis libérée sous forme de radiation Hawking, a commencé à être mieux comprise. Sous l'influence des travaux de Cumrun Vafa, Andrew Strominger, Juan Maldacena, Léonard Susskind et Edward Witten, Stephen Hawking a d'ailleurs fini par changer d'avis.

Edward Witten (Crédit : Institute for Advanced Study).
Au même moment, une approche alternative et peut-être complémentaire au problème de la gravitation quantique, la théorie de la gravitation quantique à bouclesgravitation quantique à boucles (Loop Quantum Gravity ou LQG en anglais), jetait elle aussi une vive lumière sur le problème de l'entropie des trous noirs.
D'après des chercheurs comme Abhay Ashtekar et Lee Smolin, l'espace-temps de la gravitation quantique est en fait granulaire. C'est en appliquant ces résultats à la quantificationquantification de la surface d'un trou noir que Carlo Rovelli, de l'Université de Marseille, est arrivé lui aussi à comprendre un peu mieux l'origine de l'entropie des trous noirs. Si l'espace-temps est en effet discret, cela renforce d'ailleurs l'idée de 't Hooft consistant à regarder l'Univers sous l'angle des automates cellulaires et de la théorie de l'information.

Carlo Rovelli (Crédit : John Baez).
Que ce soit pour le problème du paradoxe de l'information, ou celui du comportement holographique de l'information liée aux trous noirs, bien des choses restent encore à élucider. Le possible rayonnement de corps noir des trous noirs semble à beaucoup une clé pour explorer la physique du XXI ième siècle et l'aventure continue.
Liens
Les liens du dossier pour des cours ou des article faisant le point sur un domaine ont été regroupés ci-dessous.
Mécanique quantique et mécanique statistique
- cours de Claude Aslangul sur l'ancienne théorie des quanta.
- Cours de thermodynamique statistique de Claire Lhuillier, Eric Brunet et Redha Mazighi du laboratoire de Physique Théorique de la Matière Condensée : Université Pierre et Marie Curie