au sommaire
Un premier intérêt de la racine carrée de 2 est qu'elle constitue une porteporte d'entrée vers des pans entiers des mathématiques aussi bien anciennes que modernes : la géométrie et la théorie des nombres, mais aussi la logique, l'algèbre, l'arithmétique, l'analyse, et plus récemment l'algorithmiquealgorithmique, les structures de données, les nombres p-adiques ou encore la dynamique symbolique.

Même si, bien sûr, elle n'est pas au centre de toutes les théories qu'elle permet d'introduire, l'incroyable quantité de contextes dans lesquels la racine carrée de 2 est susceptible de fournir un fil directeur cohérent suffit à justifier que lui soit attribuée une place au panthéon des nombres. D'ailleurs, l'intention initiale de mon travail à son sujet était précisément celle-ci : utiliser la racine carrée de 2 comme point de départpoint de départ vers quelques destinations d'où peuvent s'admirer certains des plus beaux paysages mathématiques. À l'instar du mathématicienmathématicien indien du XXe siècle Srinivasa RamanujanSrinivasa Ramanujan, qui passait pour vivre au milieu des nombres comme si chacun d'eux était pour lui un ami personnel, j'ai songé un temps à prendre la racine carrée de 2 comme simple compagne de voyage pour faire partager au lecteur des aventures intellectuelles qui ne se vivent que dans le monde mathématique.

Une étude plus poussée montre que la racine carrée de 2 est bien davantage qu'un simple guide
Constante fondamentale des mathématiques, à l'image de ce que sont aux sciences physiques la vitesse de la lumière ou la charge de l'électron, la racine carrée de 2 est un nombre aux mille visages, aussi bien théoriques qu'appliqués et historiques. Bien sûr, cela ne signifie pas qu'il faille chercher à toute force un particularisme exclusif de √2 au détour de chaque résultat ou de chaque remarque.
En mathématiques en effet, il n'y a pas d'intérêt à parler d'un objet unique à l'exclusion de tous les autres. C'est en bonne partie à travers les liens qu'elle entretient avec les autres nombres que se déploient les propriétés les plus remarquables de la racine carrée de 2. Lorsqu'elle partage certaines de ses caractéristiques avec d'autres nombres, elle se fait le maillon d'une chaîne de nombres indissolublement liés par tel ou tel caractère particulier : grandeur géométrique, quantité irrationnelle, racine carrée, nombre algébrique, nombre quadratique, « k-nombre d'or »... Ces propriétés de la racine carrée de 2 éclairent chacune à leur manière l'une de ses facettes, si variées que l'on peine à trouver un autre nombre qui marquerait d'une empreinte comparable des contextes aussi différents que la musique, l'architecture ou la photographiephotographie.
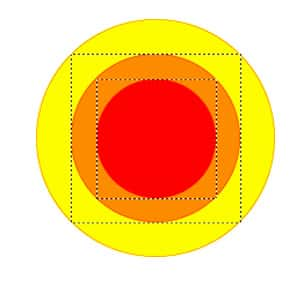
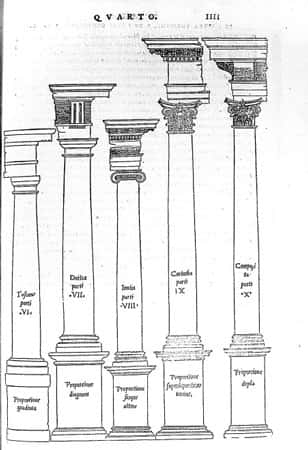
« À quand un livre sur la racine carrée de 3 ? » me demandent régulièrement quelques esprits gentiment moqueurs. On pourrait les prendre au mot : pour visiter les terres mathématiques, √3 serait un guide tout à fait acceptable, dont il est question chez Platon et Archimède aussi bien que chez l'architectearchitecte Palladio. Malgré tout, pour ce que nous en savons, la diversité dont nous parlions pour la racine carrée de 2 ne se retrouve que partiellement pour un nombre comme √3, et disparaît presque complètement pour la plupart des autres nombres.
Parmi les rares nombres, dont la multitude des aspects soit comparable à celle de la racine carrée de 2, figure le « nombre d'or », noté φ (phi), égal à (1+√5)/2 (soit environ 1,618).
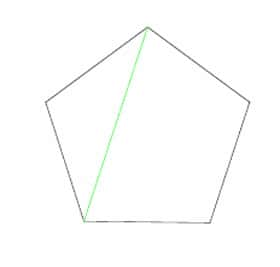
Véritable frère de la racine carrée de 2, cet Apollon des mathématiques est lui aussi présent sur le terrain des mathématiques pures comme sur celui de la réalité la plus concrète. Ces deux constantes fondamentales sont si intimement liées qu'il est difficile de décider laquelle des deux est « la plus fondamentale ». S'intéresser aux propriétés de l'une est d'ailleurs souvent utile pour mettre en relief certaines caractéristiques de l'autre. Ces liens qui se tissent entre √2 et φ, ainsi que d'autres qui s'observent entre √2 et π, montrent que les nombres remarquables, bien loin d'être des étrangers les uns pour les autres, constituent une seule et même famille.
































