au sommaire
Reprenons le triangle d'or que nous venons de construire. C'est pour ce triangle qu'EuclideEuclide, dans Les éléments démontre géométriquement la constructionconstruction d'un triangle isocèle dont chaque angle à la base est le double de l'angle au sommet et il montre la proportion « moyenne et extrême raison » du côté sur la base.

Rappelons-nous qu'ABC est appelé triangle d'or parce qu'il présente deux dimensions dont le rapport est le nombre d'or. Côté/base = Φ, ce que nous avons trouvé avec notre ficelle.
Jouons avec le triangle d'or
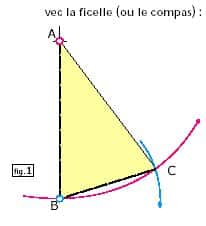
Pour construire la figure 2, partons du triangle ABC. Complétons la figure 1 en prolongeant l'arc de cercle de centre B et de rayon BC (en bleu) et en traçant aussi le cercle complet à partir du centre A.
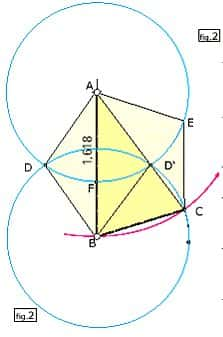
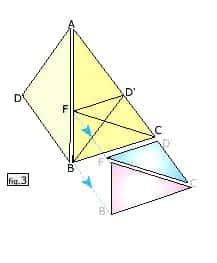
Il suffit de regarder la figure obtenue où l'on remarque :
- BC = BD' = BD = AD = AF = AD' = AE qui, pour cette figure, sera = 1. Si BC = 1, nous avons AB = AC = 1,618 (d'après ce qui précède) ;
- ABC, déjà vu, côté/base = Φ, triangle d'or dit « sublime » pour le différencier du triangle suivant ;
- ABD, base (AB)/côté (AD) = Φ, triangle d'or appelé « divin » ;
- Triangle ABD', identique à ABD avec lequel il forme un losange d'or dont la diagonale AB et un côté sont dans le rapport Φ ;
- AECBD est un pentagone régulier formé par un triangle sublime et deux triangles divins. Sa diagonale AB/le côté BC = Φ ;
- Le triangle sublime ABC peut se décomposer en deux triangles : le triangle AD'B qui est divin et le triangle BD'C qui est sublime.