au sommaire
Dans la nature, de la coquille d'escargot à la marguerite, on retrouve très souvent des motifs basés sur la suite de Fibonacci et le nombre d'or. Ce nombre est la limite de l'harmonie, sa définition.

Faisons le point après ce premier jeu, regardez bien la coquille ci-dessous.
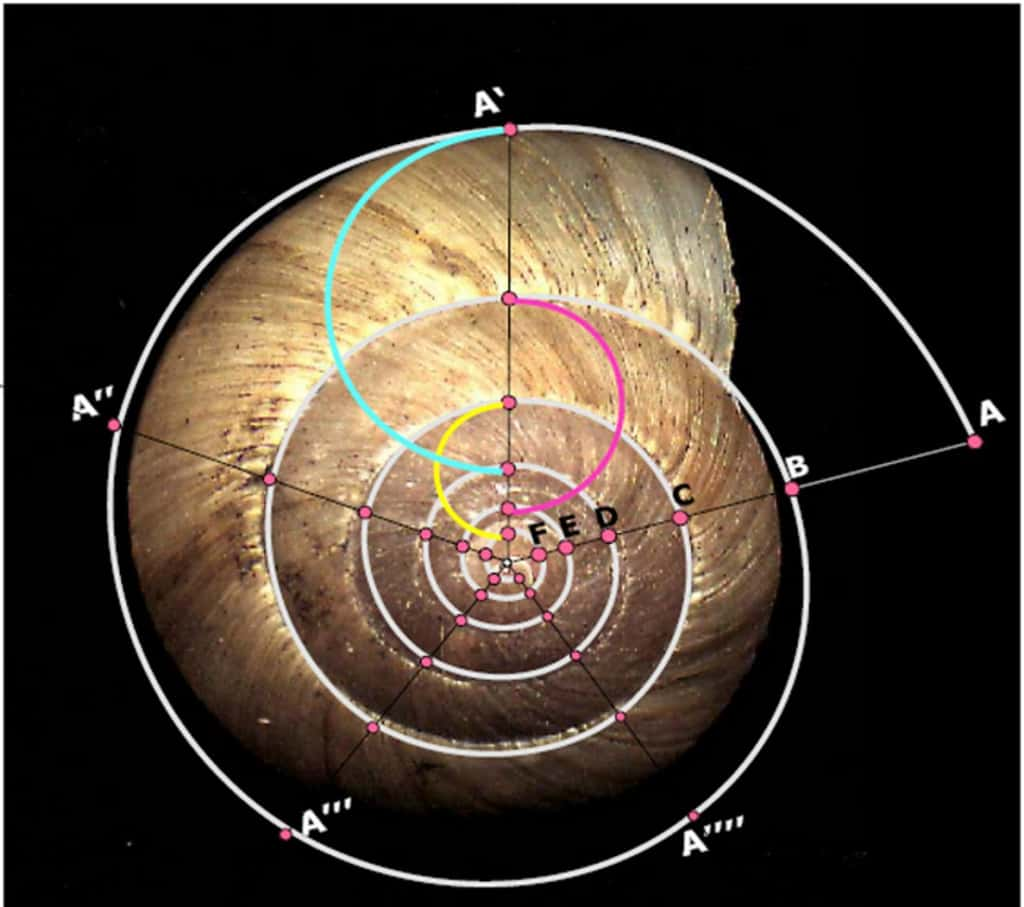
Les arcs de cercle bleu, rouge et jaune sont suffisants pour affirmer que sur un rayon (OA) l'écartement de la spire (AB) est égal à l'addition des deux écartements précédents (BC+CDCD). C'est bien vrai ? Ce que nous avons réalisé dans le premier jeu se retrouve sur un escargot ! Et c'est lié au nombre d'or !
Une suite de nombres appelée « Suite de Fibonacci »
Les longueurs que nous avons ajoutées (a et b), nous aurions pu les mesurer et nous aurions alors pu ajouter des chiffres, une méthode plus facile que des dimensions avec une ficelle. Nous aurions obtenu une suite de nombres dont chaque terme est égal à la somme des deux précédents. Une telle suite s'appelle une suite de Fibonacci, du nom du mathématicienmathématicien qui l'a publiée il y a plus de 800 ans... mais elle existait bien avant.
Les deux nombres de départ pouvant être quelconques, il y a donc une infinité de suites possibles. Pour toutes ces suites, le rapport entre deux termes consécutifs tend vers le nombre d'or Phi (= 1,618...), Phi venant de Phidias, l'architectearchitecte grec du Parthénon.
La plus simple de ces suites est celle commençant par les chiffres 1 et 1, d'où la suite classique : 1 1 2 3 5 8 13 21 34 55 89 144 233...
Ici, 1 représente une unité, qui peut être 1 mètre, 1 pied... les autres nombres représentent autant de fois cette même unité. Dans cette suite, 8/5 = 1,6 puis plus loin 55/34 = 1,617 ou encore 89/55 = 1,61818 puis 233/144 = 1,61805... Il faudrait poursuivre jusqu'à l'infini pour découvrir tous les chiffres après la virgule, et ainsi obtenir le nombre Phi, ce qui est impossible.
Deuxième jeu où l'on rencontre des surfaces d'or
Nous allons nous servir des longueurs du premier jeu, ou des nombres de la suite classique de Fibonacci pour construire la figure 1.
Soit un point A et une droite verticale passant par A. Tracer l'arc de cercle de centre A et de rayon AB (en rouge). Prendre AB = une de vos dimensions du jeu précédent, par exemple la dimension i (où AB = un nombre de la suite classique, par exemple 89, donc 89 cm à la ficelle, 89 mm au compas).
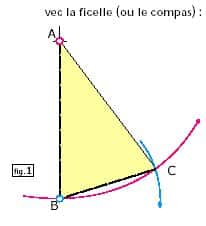
Tracer l'arc de cercle de centre B et de rayon BC (en bleu), prendre BC = votre dimension h, la première à gauche de i (où B = le premier nombre à gauche de 8, soit 55).
Joindre AC.
Le résultat est un triangle isocèle ABC appelé triangle d'or parce qu'il présente deux dimensions dont le rapport est le nombre d'or. Son côté divisé par sa base est égal à Phi : AB/BC = Φ = 1,618.
N.B : 89/55 = 1,6181818... alors que Φ = 1,61803398. La précision est très suffisante pour des tracés. Nos ancêtres se contentaient souvent du rapport 8/5 = 1,6.


































