au sommaire
L'infini n'a pas été accepté facilement, et on a longtemps espéré pouvoir s'en passer. AristoteAristote refusait l'infini actuel (ou infini en acte), c'est-à-dire pris d'un seul tenant. Il déniait toute existence physique à l'infini, mais lui reconnaissait une certaine existence mathématique, car il lui semblait nécessaire d'envisager des grandeurs de plus en plus élevées : chaque entier est suivi d'un autre ; aucun point n'est le dernier point d'une droite. Les mathématiciensmathématiciens ont tenté de se contenter de cet infini potentiel ou en tout cas de s'y ramener, en évitant autant que possible l'infini actuel.

Spirale du temps infini. © Sashkin, Fotolia

Georg Cantor a montré qu’il est possible de dénombrer l’ensemble des nombres rationnels, qui paraît plus grand que l’ensemble des nombres entiers. © Belin
EuclideEuclide, par exemple, n'énonce pas qu'il existe une infinité de nombres premiers, mais que « les nombres premiers sont en plus grande quantité que toute quantité de nombres premiers proposée », ce qu'il démontre en établissant que si des nombres premiers sont donnés par avance p1, p2,... pk, on peut en construire un (le plus petit diviseur premier de p1 p2... pk+1) qui sera différent de tous ceux qui étaient donnés.
La raison profonde de cette méfiance vis-à-vis de l'infini actuel est le paradoxe de la réflexivité : si un ensemble est infini, il est possible de le mettre en correspondance un à un (on dit aussi bijective, ou biunivoque) avec une de ses parties propres (c'est-à-dire différente de lui-même). La relation qui associe n2 au nombre n, par exemple, établit une correspondance bijective entre les nombres entiers 0, 1, 2, 3,... et les carrés 0, 1, 4, 9,... lesquels sont pourtant moins nombreux.
Le même problème surgit à propos du segment des nombres réels compris entre 0 et 1 (noté aujourd'hui [0, 1]) et celui des nombres réels compris entre 0 et 2 (la correspondance bijective est celle qui, à x, associe 2x) ; généralisant, on met sans aucune peine en correspondance bijective deux segments de droite AB et A'B' quelconques. Plus gênante encore, la correspondance qui à x associe 1/(x+1), car elle met en correspondance bijective l'intervalle les nombres réels compris entre 0 et 1, noté ]0, +1[, et l'ensemble des nombres réels positifs, noté ]0, +∞[.
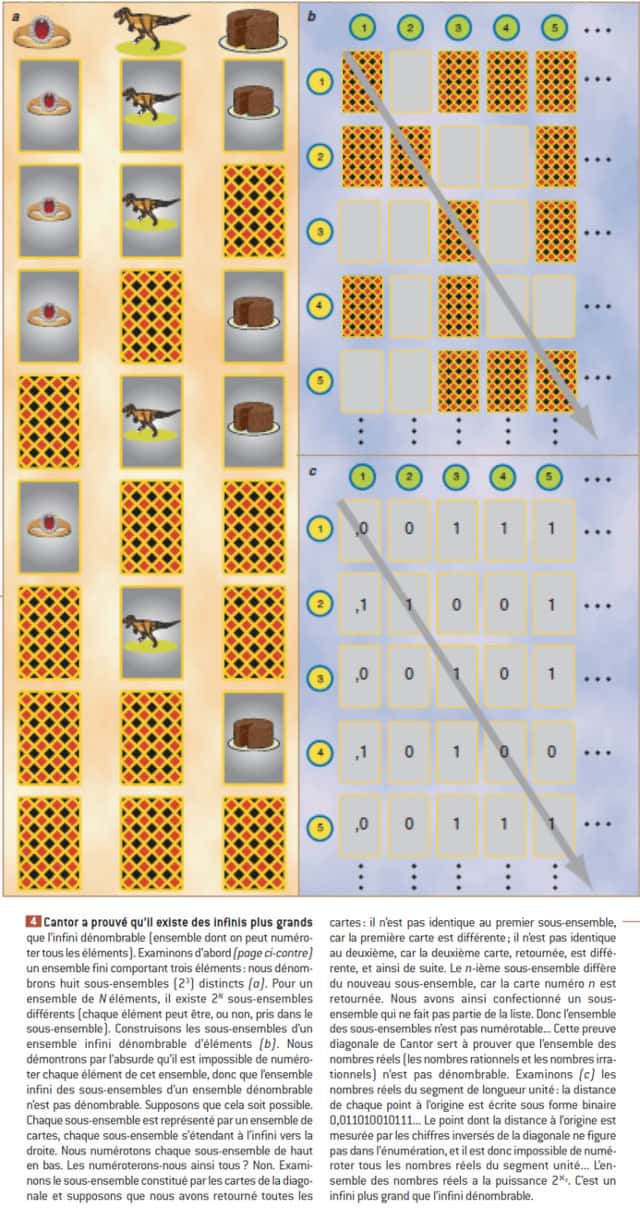
Cette démonstration de Cantor permet de prouver l’existence d’infinis plus grands que l’infini dénombrable. © Belin
En quoi le paradoxe de la réflexivité est-il un paradoxe, nous demandons-nous aujourd'hui ? C'est un paradoxe, car le principe du tout et de la partie qui indique que « le tout est plus gros que la partie » y est mis en défaut. On n'imagine pas de renoncer à une vérité aussi claire. On craint que notre raison ne puisse résister à la remise en cause d'un tel principe immédiat. Reconsidérer ce principe du tout et de la partie apparaîtrait d'une audace insensée, et c'est pourquoi on a bien souvent préféré conclure que seul un être infini lui-même, Dieu par exemple, peut penser l'infini. L'Église s'opposait d'ailleurs à toute tentative des hommes de penser l'infini actuel. Saint Thomas d'Aquin considérait que quiconque pensait concevoir l'infini actuel entrait en concurrence avec la nature unique et absolument infinie de Dieu.
Il faudra 2.000 ans pour franchir cet obstacle. Le principe du tout et de la partie qui, à vrai dire, n'est guère utile en mathématiques, devait être reconsidéré : ce principe éminemment paradoxal empêchait tout progrès dans la compréhension de l'infini actuel.
Cette audace sera le fait du philosophe mathématicien tchèque Bernhard Bolzano (1781-1848), dont l'ouvrage Les paradoxes de l'infini, publié après sa mort en 1851, envisage des correspondances bijectives entre une totalité et l'une de ses parties propres, sans s'en émouvoir. Au contraire, Bolzano propose de voir dans ces correspondances la caractéristique des totalités infinies, ce qui revient à abandonner, pour les totalités infinies, le principe du tout et de la partie. Plus tard, le mathématicien allemand Richard Dedekind (1831-1916) définira qu'un ensemble est infini s'il peut être mis en bijection avec une de ses parties propres : aujourd'hui, on adopte souvent cette définition en théorie des ensembles pour définir un ensemble infini.
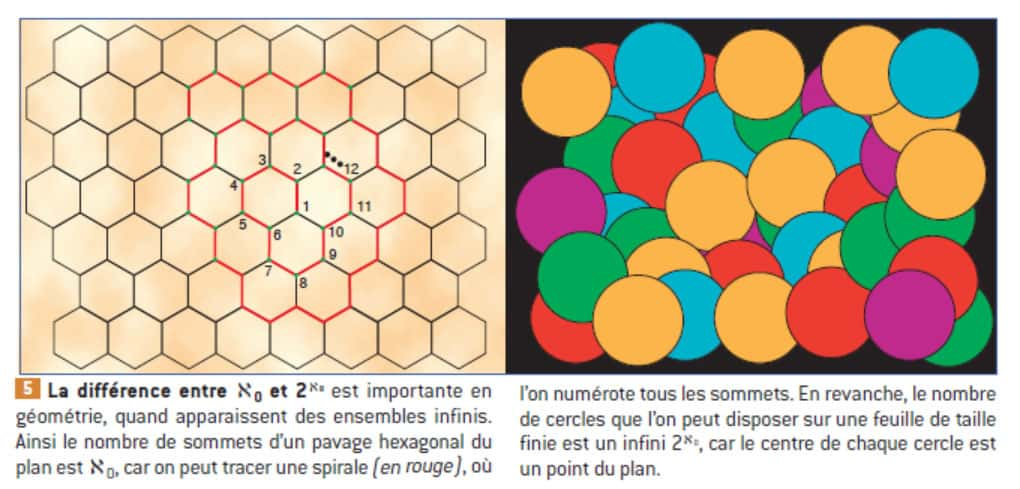
La différence entre ces deux infinis est importante en géométrie. © Belin
Avant Bolzano, Gottfried Leibniz avait défendu l'idée de l'infini actuel. « Je suis tellement pour l'infini actuel qu'au lieu d'admettre que la nature l'abhorre, comme l'on dit vulgairement, je tiens qu'elle l'affecte partout, pour mieux marquer la perfection de son Auteur » (Leibniz, Opera omnia studio Ludov. Dutens, tome II, partie X). Bolzano place cette citation en exergue de son ouvrage révolutionnaire.

Cantor a proposé et détaillé une notation pour les infinis. © Belin
Cependant, l'infini actuel que défend Leibniz est différent de celui des totalités infinies considérées actuelles dans le problème du paradoxe de la réflexivité. Leibniz défend plutôt un infini philosophique, celui du monde physique pris comme un tout. L'infiniment petit (qui est confronté à d'autres paradoxes qu'on utilise parfois pour attaquer les nouvelles méthodes de calcul que Leibniz défend) ne saura vraiment trouver une place confortable et assurée en mathématiques qu'en se débarrassant de son objectualité, c'est-à-dire quand on ne parlera plus des infiniment petits comme d'objets mathématiques, mais comme de limites. Les mathématiciens du XXe siècle sauront redonner aux infiniment petits un statut d'objet authentique. La méthode utilisée au XIXe siècle pour rendre rigoureux le calcul infinitésimal est un renoncement à l'infini actuel, auquel on substitue un infini potentiel, celui de quantités qui s'approchent de plus en plus de leur limite.

Les découpages paradoxaux découverts par Stephan Banach et Alfred Tarski choquent le sens commun. © Belin
Le prince des mathématiciens, Gauss (1777-1855), exprimant le sentiment partagé par la communauté mathématique de son époque, écrivait par exemple : « Je conteste qu'on utilise un objet infini comme un tout complet ; en mathématiques, cette opération est interdite ; l'infini n'est qu'une façon de parler. »

Bolzano, puis Gauss et Leibniz, ont amené notre conception actuelle de l’infini. © Belin
On peut donc affirmer que malgré quelques tentatives diverses pour fonder une science mathématique de l'infini, c'est Bolzano et nul autre qui, en affrontant le paradoxe de la réflexivité, a le premier ouvert la voie à ce qui aujourd'hui est notre conception de l'infini mathématique pris comme un tout.