au sommaire
La théorie des catastrophes est la théorie mathématique des modifications spectaculaires ou soudaines. Les mathématiciensmathématiciens Tim Poston et Ian Stewart fournissent des exemples : « Le grondement d'un tremblement de terretremblement de terre, la densité critique de population en dessous de laquelle certaines créatures se développent comme sauterellessauterelles et au-dessus comme criquets... Le rythme de reproduction change brusquement, et ne cesse de doubler, de façon cancéreuse. Un homme est pris d'une vision sur le chemin de Damas ».

La théorie des catastrophes est la théorie mathématique des modifications abruptes, comme le comportement des sauterelles lorsque la densité de population s’accroît. La recherche laisse penser que les nuées soudaines sont provoquées par les contacts accrus des pattes arrière des insectes sur une période de quelques heures. Les nuées elles-mêmes peuvent se composer de milliards d’insectes. © Taken, CCO
Histoire de la théorie des catastrophes
La théorie des catastrophes a été développée par le mathématicien français René Thom (1923-2002) dans les années 1960. Elle fut ensuite popularisée dans les années 1970 par le mathématicien Christopher Zeeman, qui continua à appliquer la théorie aux sciences comportementales et biologiques. René Thom reçut la médaille Fields en 1958 pour ses travaux en topologie, l'étude des formes géométriques et de leurs relations.
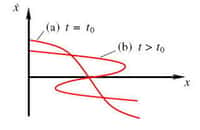
La théorie des catastrophes concerne généralement les systèmes dynamiques qui décrivent la dépendance temporelle de certaines quantités (comme le battement du cœur) et la relation de ces systèmes avec la topologie. Elle se concentre en particulier sur certains types de « points critiques » dans lesquels la dérivée première d'une fonction et une ou plusieurs dérivées supérieures sont égales à zéro. David Darling écrit : « De nombreux mathématiciens ont entrepris l'étude de la théorie des catastrophes, qui connut un certain temps un engouement extraordinaire ; cependant, elle n'atteignit jamais le succès la théorie du chaos, car elle n'est pas parvenue à se montrer à la hauteur de ses promesses en matière de prédictions utiles ».
L'hommage de Salvador Dali à René Thom
La recherche de René Thom visait à mieux comprendre comment les actions continues (comme un comportement régulier et stable dans les prisons ou entre deux pays) pouvaient conduire brusquement à une modification discontinue (mutinerie ou guerre).
Il montra comment de tels phénomènes pourraient être décrits sous la forme de surfaces mathématiques abstraites, sous des noms tels que le papillon ou la queue d'arondearonde. Le dernier tableau de Salvador Dali, Queue d'aronde (1983), s'inspirait de la théorie des catastrophes. Son tableau intitulé Enlèvement topologique d'Europe : Hommage à René Thom (1983) décrivait un paysage fracturé, ainsi que l'équation qui l'expliquait.