au sommaire
La théorie de Ramsey a partie liée avec la recherche d'ordre et de modèles au sein des systèmes. Paul Hoffman écrit à son sujet : « L'idée sous-jacente à la théorie de Ramsey est l'impossibilité d'un désordre complet... Si la recherche s'effectue au sein d'un univers suffisamment large, il est possible de trouver n'importe quel "objet" mathématique. La théorie de Ramsey souhaite connaître le plus petit univers qui contienne un objet donné ».

Qu'est-ce que la théorie de Ramsey ? © Maproom GFDL
La théorie de Ramsey doit son nom au mathématicienmathématicien anglais Frank Plumpton Ramsey (1903-1930). Cette branche des mathématiques a commencé à se développer en 1928, quand Frank Ramsey s'est intéressé à un problème de logique.
Comme le sous-entend Paul Hoffman, la théorie de Ramsey recherche le nombre nécessaire d'éléments d'un système pour qu'une propriété particulière se vérifie. À l'exception de certains travaux intéressants de Paul Erdös, ce n'est qu'à compter de la fin des années 1950 que la théorie de Ramsey a réellement progressé.
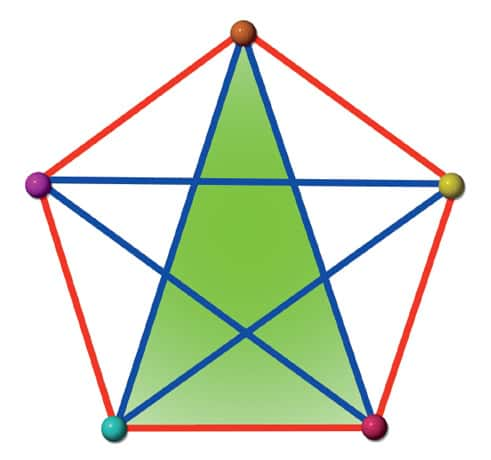
Chaque point est connecté aux quatre autres à l’aide de traits de couleur rouge ou bleue. Dans cette description, il n’existe pas de triangle dont tous les côtés soient exclusivement bleus ou exclusivement rouges. Six points sont nécessaires pour être certain d’obtenir un triangle entièrement bleu ou entièrement rouge. © Dunod, droits réservés
La théorie de Ramsey et le principe du pigeonnier
Un exemple de l'une des applications les plus simples est le principe du pigeonnier qui établit que si nous avons m pigeonniers et n pigeons, nous pouvons être certain qu'au moins un pigeonnier abrite plusieurs pigeons si n > m. Autre exemple, plus complexe, celui d'une dispersion de n points sur une feuille de papier. Chaque point est relié à tous les autres points par un trait de couleurcouleur rouge ou bleue. Le théorèmethéorème de Ramsey montre que n doit être égal à 6 pour être sûr de la présence d'au moins un triangle bleu ou un triangle rouge.
Le problème des groupes
Une autre façon d'envisager la théorie de Ramsey concerne le problème dit des groupes. Par exemple, quelle taille minimale doit avoir un groupe pour qu'au moins trois de ses membres soient (deux à deux) des étrangers ou qu'au moins trois d'entre eux soient deux à deux des connaissances mutuelles ? La réponse est 6. En revanche, il est beaucoup plus difficile de trouver la taille d'un groupe incluant au moins quatre amis mutuels ou quatre étrangers mutuels. Il se peut même que l'on ne parvienne jamais à résoudre le problème dans le cas de groupes beaucoup plus grands.