Symétries et applications mathématiques

Les correspondances qui définissent une symétrie se traduisent mathématiquement par des applications T : E → E internes à l'ensemble E des éléments que l'on cherche à décrire.

Fleur Passiflora caerulea. © Petar Miloševic, Wikimedia commons, CC by-sa 4.0

Par exemple, une symétrie miroir associe P à T(P) = P'. Appliquer deux fois une symétrie miroir consiste à ne rien modifier, mais ce n'est pas une propriété générale. On étend la notion de symétrie à des applications dont les n-ièmes itérées peuvent conduire à de plus longues suites P, P', P'', P''', etc. Ainsi, en prenant pour T une rotation plane d'un q-ième de tour autour d'un point O, on engendre à partir de P (différent de O) une suite finie de q points distincts sur le cercle de rayon OP si q est entier, et une suite infinie de points, dense sur le cercle, si q est irrationnel.

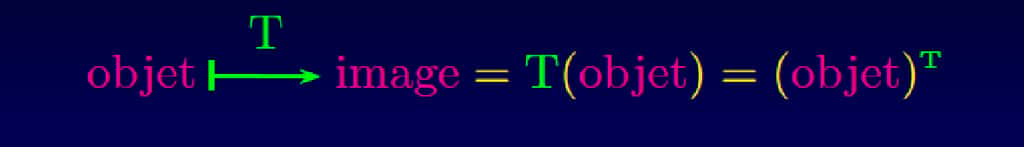
Différentes manières de noter mathématiquement la transformation d’un objet en son image. © Amaury Mouchet

Les applications

Plus généralement, une symétrie est associée à un ensemble G d'applications (par exemple les itérés comme précédemment) et les quatre facettes décrites précédemment se précisent en :

• (i) une transformation : on change x en T(x) (sans garder x) pour une seule application T de G ;
• (ii) un regroupement : on engendre l'ensemble S(x) obtenu en gardant toutes les images T(x) de toutes les applications T de G ;
• (iii) une invariance : l'action de n'importe quel T de G sur S(x) redonne l'ensemble S(x) : chaque élément n'est pas forcément invariant, mais l'ensemble S(x), lui, reste globalement invariant.
• (iv) une projection (les mathématiciens préféreraient parler de section, en réservant exclusivement le terme de projection aux applications égales à leurs itérées) : plutôt que de spécifier chacun des éléments des ensembles invariants (dits encore globalement invariants ou symétriques) S(x₁), S(x₂),..., S(x_n), on se donne un seul point par S, c'est-à-dire que formellement, la projection se traduit donc par un choix d'application S → x où l'on choisit un x représentatif de chaque S. L'invariance de S est brisée, car x n'est pas invariant. C'est pourquoi on rencontre le terme de brisure de symétrie (symmetry breaking).

 
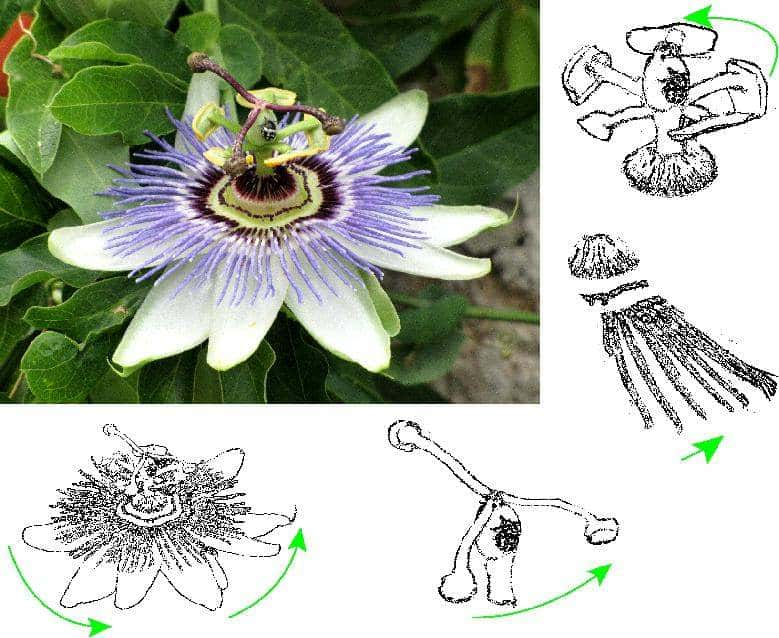
Dans la nature la symétrie de rotation d'une fraction de tour se retrouve fréquemment comme ici, dans la fleur de la passiflore. © Amaury Mouchet, Dunod

Le regroupement, opération inverse de la projection, permet, une fois données les règles qui définissent T, de classer les éléments reliés par symétrie, puis de supprimer la partie redondante de l'information contenue dans les différentes classes en considérant que chaque élément de la classe est équivalent aux autres. Pour cela, on introduit la notion fondamentale [voir la note en bas de page, NDLRNDLR] de relation d'équivalence qui désigne une relation binairebinaire symétrique, réflexive, transitive entre les éléments d'un ensemble E.

Plus précisément, si x et y sont deux éléments de E, la notation x ~ y signifie que x est relié à y. On définit alors les propriétés suivantes :

• (a) Réflexivité : tout x de E est relié à lui-même : x ~ x ; 
• (b) Symétrie (ce n'est pas un hasard si l'on retrouve ce terme ici) : pour tous x et y de E, si x ~ y, alors y ~ x ; 
• (c) Transitivité : Pour tous x, y et z de E, si x ~ y et y ~ z, alors x ~ z. 

À partir d'un ensemble d'applications G, on peut donc définir la relation binaire par : x ~ y si et seulement s'il existe dans G une application T telle que y = T(x). Dire que cette relation est réflexive, c'est dire que pour tout x, il existe une application T pour laquelle x est invariant. En particulier il suffit que :

• (a') G contienne l'identité.

Pour avoir la symétrie, il suffit que :

• (b') toute application considérée T soit inversible et que son inverse T^-1 soit dans G.  

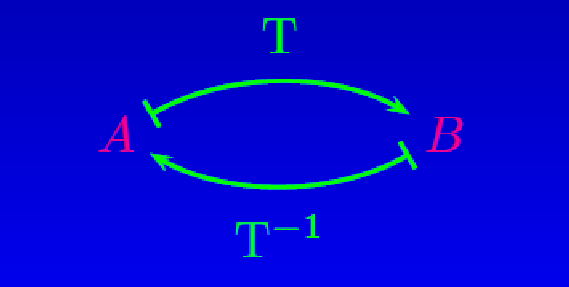
L’application T transforme A en B, et son inverse B en A. © Amaury Mouchet

Enfin, pour avoir la transitivité, il suffit d'avoir une loi de composition interne :

• (c') Si T₁ et T₂ sont dans G, alors la composition T₁ o T₂ aussi.

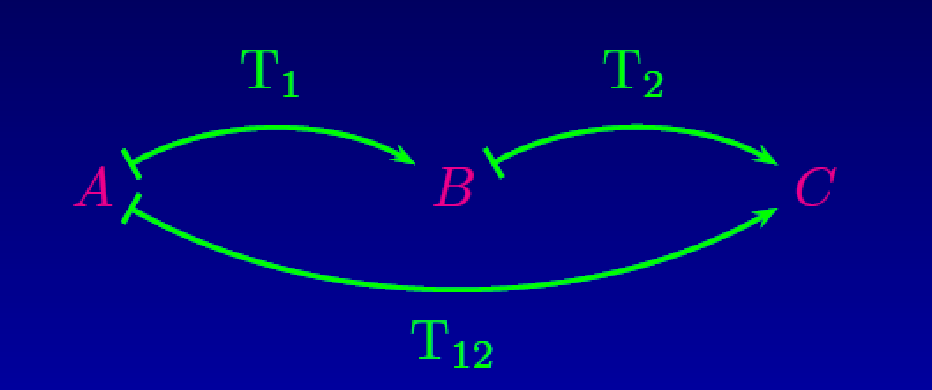
L’application T₁ transforme A en B, T₂ fait de même avec B en C, et la composition permet de passer de A à C. © Amaury Mouchet

De plus, la loi de composition des applications est toujours associative, autrement dit :

• (d') pour tout triplet de transformations de G, on a (T₁ o T₂) o T₃ = T₁ o (T₂ o T₃).

Les propriétés (a'), (b'), (c') et (d') caractérisent alors l'ensemble T comme étant un groupe. Les classes d'équivalence sont alors précisément définies par les ensembles S définis en (ii).

L'ensemble des classes de E, appelé ensemble quotient, noté E/~ pour bien souligner que l'on divise (quotiente) E en classes, est plus petit que E, sans que l'on ait perdu en richesse : on transpose les opérations de E directement sur les classes S, ces dernières étant considérées comme les nouveaux éléments de base, plus abstraits puisque l'on peut alors aisément oublier comment ils ont été définis. Parmi une multitude d'exemples, on peut retenir le cas des nombres rationnels : un nombre rationnel positif peut être considéré comme une classe d'équivalence regroupant tous les couples d'entiers naturels (E = N²) ayant un multiple commun ; (p,q) dans N², est équivalent à (p',q') si et seulement si pq' = p'q. En géométrie euclidienne, un vecteur peut être vu comme une classe d'équivalence regroupant toutes les paires de points formant des parallélogrammesparallélogrammes.

Note : pas uniquement en mathématiques, puisque si l'on y réfléchit, elle est inhérente à toute forme de pensée rationnelle et permet de préciser ce que l'on entend par abstraction. Ce que vous désignez par « ce livre » ou par « la planète Mars » représente une classe d'équivalence qui fait abstraction des transformations inévitables comme une rotation, un changement d'éclairage, les incrustations de poussières, vos modifications synaptiques, le mouvementmouvement des luneslunes de JupiterJupiter, etc. Tout l'art consiste à identifier les paramètres les plus pertinents et à supprimer les innombrables autres. C'est une caractéristique de la pensée rationnelle que d'établir ainsi des modèles susceptibles d'être mis à l'épreuve de l'expérience. Élaguer le surplus d'information est nécessaire pour identifier les propriétés émergentes comme la forme d'un objet ou, plus quantitativement, celles issues de moyennes d'ensemble comme, en physiquephysique statistique, la pressionpression, la température, la compressibilité, la transparencetransparence, etc. Cette difficile opération va dans le sens opposé à celui de la démarche purement réductionniste qui, elle, décompose un tout en parties ; elle reste néanmoins une tâche incontournable pour qui prétend comprendre.