Il avait introduit le temps imaginaire en cosmologie avec Hawking : James Hartle est décédé

Le département de physique de l'UC Santa Barbara a fait savoir il y a presque un mois maintenant que James Hartle était décédé à l'âge de 83 ans. Né le 20 août 1939 à Baltimore, sur la côte est des États-Unis, il s'est éteint paisiblement en Suisse alors qu'il luttait contre la maladie d'Alzheimermaladie d'Alzheimer. Le grand public le connaît sans doute implicitement pour l'une de ses contributions majeures à la cosmologie quantique, le fameux modèle de Hartle-Hawking dont Futura a parlé à plusieurs reprises notamment dans le précédent article ci-dessous auquel nous renvoyons, et aussi aux vidéos qui vont suivre.

Le grand public le connaît aussi peut-être en raison de l'ouvrage que Thomas Hertog a récemment publié et qui parle justement des développements de la théorie de James Hartle et Stephen HawkingStephen Hawking. Thomas Hertog a obtenu son doctorat à l'Université de Cambridge sous la direction de Hawking et il est actuellement professeur de physique théorique à l'Université catholique de Louvain, en Belgique.

Stephen Hawking, James Hartle, Thomas Hertog et l'Univers sans frontière

Le modèle de Hartle-Hawking tente de donner une réponse à la question de l'origine de l'Univers et de son contenu en galaxies en utilisant une théorie reposant sur une des formulations de la mécanique quantiquemécanique quantique que l'on appelle "l'intégrale de chemin" du prix Nobel de physique Richard Feynman. Hartle a raconté comment il s'est trouvé fasciné très tôt au cours de ses études -- alors qu'il était encore en licence à l'Université de Princeton et avait rien de moins que John Wheeler comme professeur -- par la formulation de la théorie quantique découverte par Feynman alors qu'il était le thésard de Wheeler à Princeton. Cela lui permettra plus tard d'utiliser cette formulation pour déduire d'une façon nouvelle le rayonnement des trous noirstrous noirs et préciser leurs propriétés thermodynamiquesthermodynamiques en compagnie de Hawking en 1976, ce qui le conduira à collaborer une fois de plus avec Hawking, mais cette fois-ci sur le mystère des singularités en cosmologie issues des travaux du prix Nobel de physique Roger Penrose, donnant donc naissance au modèle de Hartle-Hawking éliminant la singularité cosmologique primordiale grâce à la mécanique quantique.

La théorie de Hartle et Hawking fait introduire au tout début du Big BangBig Bang, si l'on peut dire, un changement de l'état de l'espace-tempsespace-temps qui devient purement espace en raison de l'apparition d'une composante dite imaginaire du temps, c'est-à-dire en fait à la prise en compte des nombres complexes en mécanique quantique comme un ingrédient fondamental de la réalité et pas comme une simple astuce mathématique simplifiant des calculs avec des nombres ordinaires.

L'impact de la cosmologie sur la mécanique quantique

De manière intéressante, les travaux d'Abhay Ashtekar et Carlo Rovelli, portant sur une des formulations possibles d'une théorie quantique de la gravitationgravitation et qui a donné lieu à la découverte de la théorie dite de la cosmologie quantique à boucles, prédisent eux aussi une phase avec un temps imaginaire au « début » quantique du Big Bang classique.

Après Princeton, James Hartle avait continué ses études en master de physique aux fameux Caltech où enseigne précisément Feynman, ce qui va lui permettre au début des années 1960 de suivre ses cours sur la gravitation et d'approfondir ses connaissances sur l'intégrale de Feynman (il existe un célèbre ouvrage à ce sujet). James Hartle écrira plus tard lui aussi un cours de physique sur la gravitation pour les débutants en master.

Mais c'est avec un autre prix Nobel de physique, Murray Gell-Mann, qu'il va passer sa thèse et elle portera sur la théorie des étoilesétoiles relativistes, tout comme à ce moment-là aussi, Kip Thorne, mais sous la direction de Wheeler, qui décrochera par la suite un prix Nobel de physique pour ses travaux sur les ondes gravitationnellesondes gravitationnelles. Rappelons qu'à ce moment-là, on venait tout juste de découvrir les quasarsquasars mais pas encore le rayonnement fossilerayonnement fossile. L'avis de beaucoup de chercheurs, sauf du calibre de Wheeler, Gell-Mann et Feynman, était encore que les études en relativité générale étaient sans avenir car les équationséquations d'EinsteinEinstein étaient trop difficiles à résoudre et en général ne débouchaient sur quasiment rien de mesurable et d'observable, à part en ce qui concerne l'expansion du cosmoscosmos observable.

Hartle fera équipe par la suite avec Gell-Mann pour tirer au clair l'applicationapplication des lois de la mécanique quantique à l'Univers tout entier. En effet, l'interprétation standard de la mécanique quantique appliquée à un système physique décrit les mesures qu'un observateur fait de l'extérieur de ce système. L'observateur faisant partie de l'Univers qu'il observe, en quel sens peut-on donc appliquer les lois de la mécanique quantique à celui-ci ?

Hartle et Gell-Mann vont utiliser pour cela l'interprétation dite des histoires consistantes (également appelées histoires décohérentes ou histoires rationnelles) notamment proposée et développée par Roland OmnèsRoland Omnès et Robert B. Griffiths. D'autres chercheurs préfèrent utiliser la théorie des mondes multiples d’Everett.

Le communiqué de l'UC Santa Barbara annonçant le décès de James Hartle le 17 mai 2023 explique que « Jim était intellectuellement curieux et un lecteur éclectique, appréciant l'étude de l'archéologie du Moyen-Orient et maya, du cunéiformecunéiforme sumérien, de l'histoire coloniale américaine, de la littérature russe, de la biologie évolutive et des figures religieuses féminines excentriquesexcentriques du XIX^e siècle. Il aimait la musique classique et en particulier l'opéra, voyageait beaucoup et avec curiosité, et était un grand conteur d'anecdotes bien conçues et compositeur de toasts appropriés et amusants ».

Big Bang : le modèle de Hartle-Hawking est-il faux ?

Article de Laurent SaccoLaurent Sacco, publié le 20 juin 2017

Le modèle de Hartle-Hawking est un modèle de cosmologie quantique très populaire mais il souffre de problèmes mathématiques. Trois physiciensphysiciens, dont le célèbre Neil Turok, ont tenté de résoudre ces problèmes. Aujourd'hui, ils pensent avoir montré que le modèle de Hartle-Hawking conduit à des conséquences en contradiction avec les observations du rayonnement fossile. La théorie du Big Bang de Stephen Hawking pourrait donc être fausse.

L'année 2015 fut marquée par le centenaire de la formulation finale de la théorie de la relativité générale par Einstein. Cette année 2017, nous pouvons célébrer deux autres centenaires : celui de la formulation du premier modèle de cosmologie relativiste et celui de la découverte de l'effet laser, également par Einstein ; cette découverte a posé les bases de la mécanique des matrices de Heisenberg, un des piliers de la mécanique quantique.

En 1970, Roger PenroseRoger Penrose et Stephen Hawking ont publié un théorèmethéorème montrant qu'appliquée à la théorie du Big Bang, la théorie d'Einstein amenait inexorablement à la conclusion que notre univers devait être né d'une singularité de l’espace-temps. Toutefois, aucun de ces chercheurs n'était dupe : leur théorème montrait simplement l'effondrementeffondrement du pouvoir prédictif de la théorie de la gravitation d'Einstein tant qu'on ne cherchait pas à la rendre quantique. Or, tout comme les électronsélectrons d'un atomeatome étaient sauvés de l'effondrement inévitable sur le noyau en physique classique par les équations de la mécanique quantique, on devait s'attendre à ce que la singularité cosmologique soit, elle aussi, supprimée par ces équations appliquées à la nature et la dynamique de l'espace-temps. Mais, pour le montrer, il fallait aller au-delà de la théorie de la relativité généralerelativité générale.

Heureusement, une théorie quantique de la gravitation était déjà en cours d'élaboration pendant les années 1960. John Wheeler, l'un des pionniers de la physique des trous noirs, et Bryce DeWitt, l'époux de la physicienne et mathématicienne française Cécile DeWitt-Morette, étaient arrivés à découvrir une équation à la base de la cosmologie quantique, la fameuse équation de Wheeler-DeWitt (WD).

La cosmologie quantique et les solutions de l'équation de Wheeler-DeWitt

Cette équation est malheureusement fort difficile à résoudre, sauf si elle est appliquée à des modèles cosmologiques très simplifiés. De grandes classes de solutions ont été trouvées dans le cadre de la théorie de la gravitation quantique à bouclesgravitation quantique à boucles. Au début des années 1980, Stephen Hawking, fort des succès qu'il avait rencontrés en appliquant les travaux du prix Nobel Richard FeynmanRichard Feynman en théorie quantique des champs au cas de l'évaporation des trous noirs, a cherché, lui aussi, à utiliser cette équation pour comprendre le début de l'univers. Avec son collègue James Hartle, Stephen Hawking a dont tenté de résoudre, de façon au moins approchée, l'équation de WD dans des cas simples à l'aide de l'intégrale de chemin de Feynman.

La stratégie semblait prometteuse car les équations de la relativité générale sont des analogues des équations de Yang-MillsYang-Mills à la base du modèle standardmodèle standard en physique des particules. Or, le prix Nobel Gerard 't Hooft avait fortement contribué à montrer que l'intégrale de Feynman était un outil exceptionnellement efficace et pratique pour faire des calculs de théorie quantique des champs avec les équations de Yang-Mills.

De fait, en transposant les techniques qui marchaient en physique des particules au traitement quantique de l'espace-temps en cosmologie, Hawking et Hartle ont émis une proposition en 1983 qui allait faire grand bruit. Ils ont ainsi avancé des arguments permettant de supprimer naturellement la singularité initiale, mais au prix de considérer que la nature de l'espace-temps pouvait profondément changer au voisinage de la naissance du Big Bang. Dans les équations, le temps, au lieu d'être décrit par des nombres réels, était décrit par une généralisation de ces nombres que les mathématiciensmathématiciens ont appelé « des nombres complexes » et qui sont à la base de la fameuse équation de Schrödingeréquation de Schrödinger, l'un des postulatspostulats fondamentaux de la mécanique quantique.

Plus précisément, le temps devenait alors « imaginaire pur », dans le jargon des mathématiciens, ce qui revenait à dire que l'espace-temps à 4 dimensions devenait de l'espace à 4 dimensions. Au lieu de « débuter », par un point de densité infini et avec une courbure également infinie de l'espace-temps, le cosmos aurait alors émergé d'une géométrie quantique floue, comme le sont les trajectoires des particules dans un atome. Une image de cette géométrie serait alors celle de la surface d'une sphère sans frontière ni bord. Il est possible de se déplacer sur cette surface sans rencontrer d'obstacle, ce qui n'est pas le cas sur celle d'un cônecône, puisque son sommet est précisément une singularité de la géométrie, ou encore sur la surface d'un cylindre qui possède deux bords.

L'effet tunnel et le temps imaginaire en cosmologie quantique

La proposition sans frontière (No boundary proposal) avec temps imaginaire de Hartle-Hawking allait fasciner par son élégance et parce qu'elle proposait une solution au problème de la naissance du temps. Une variante de cette cosmologie quantique a été proposée par le physicien russe Alexander Vilenkin, également pionnier de la théorie de l'inflation éternelle. Vilenkin a développé une idée en germegerme dans la théorie de l'atome primitif de Lemaître, conçu comme une sorte de noyau subissant une désintégration radioactive par effet tunneleffet tunnel.

Il se trouve que le temps imaginaire intervient d'une certaine façon dans la théorie de l'effet tunnel quantique et il est donc possible, comme l'ont fait Hartle et Hawking, d'y voir plus qu'une astuce de calcul mais bien un changement dans la nature de l'espace-temps. La théorie de Vilenkin suggère donc que l'univers a fait une sorte de saut par effet tunnel quantique d'un état qui n'est ni espace ni temps (qui peut être abusivement appelé « le néant » mais qui suppose tout de même l'existence préalable des lois de la physique) directement dans l'espace-temps primordial.

Un modèle en deux dimensions de l'espace-temps proche du Big Bang dans le cadre du modèle de cosmologie quantique de Hartle-Hawking semblait prédire un espace-temps avec un contenu très homogène et lisse au début de son existence. C'est le modèle de gauche. Mais ses prédictions seraient plutôt conformes au modèle de droite, avec des fluctuations de température et de la géométrie de l'espace-temps tellement considérables qu'elles ne ressemblent pas à ce qui est observé. © J.-L. Lehners, Max Planck Institute for Gravitational Physics

Malheureusement, ces deux théories de cosmologie quantique souffrent de problèmes qui sont particulièrement bien définis dans le cadre de l'intégrale de chemin de Feynman. Les calculs ne sont mathématiquement pas très bien fondés et des critiques se sont donc rapidement élevées à leur sujet, par exemple de la part de Roger Penrose. (Toutefois, certains calculs menés dans le cadre de la théorie de la cosmologie quantique à boucles prédisent eux aussi une phase primitive de l'univers avec un temps imaginaire, comme l'a expliqué Aurélien Barrau sur son blogblog.)

La cosmologie quantique et le rayonnement fossile

Neil Turok et Job Feldbrugge, des physiciens du Perimeter Institute, au Canada, en collaboration avec Jean-Luc Lehners, de l'Albert Einstein Institute, en Allemagne, pensent être arrivés à surmonter certaines de ces difficultés en utilisant ce que les mathématiciens appellent « la théorie de Picard-Lefschetz », comme les chercheurs l'expliquent dans plusieurs publications sur arXiv. Cette théorie permet notamment de traiter les idées de Hartle, Hawking et Vilenkin dans un cadre plus large où elles fusionnent. Cette théorie permet aussi de mieux mettre sous contrôle les calculs avec l'intégrale de Feynman dans lesquels l'espace-temps peut être décrit par les nombres complexes qui contiennent les nombres réels et imaginaires comme des sous-ensembles distincts.

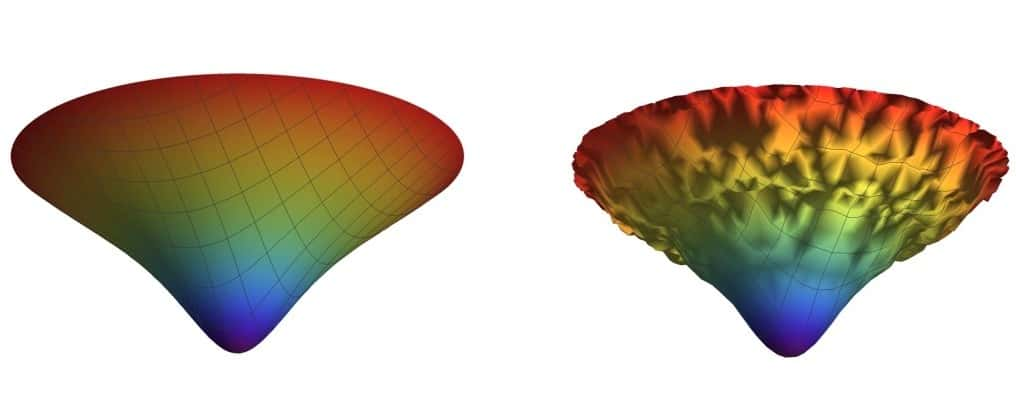
Mauvaise surprise selon ces trois chercheurs. La théorie qui fait débuter en quelque sorte l'espace-temps avec une géométrie aussi lisse que la surface d'une sphère, ce qui est en particulier le cas du modèle de Hartle-Hawking, conduit en fait à des fluctuations de la courbure de l'espace-temps qui sont très fortes et l'on devrait donc observer des fluctuations de température également très fortes dans le rayonnement fossile. Or, comme nous le savons depuis les observations de Cobe, et encore plus avec celles de PlanckPlanck, ce n'est absolument pas le cas.

Est-ce la fin du modèle sans bord de Hartle-Hawking ? Pas sûr ! James Hartle a contre-attaqué avec des collègues dans une récente publication sur arXiv. Le débat ne fait probablement que commencer et, tant que nous n'aurons pas une vraie théorie de la gravitation quantique, il risque de durer encore longtemps.