au sommaire

Itzhak Bars (Crédit : University of Southern California).
Quelques rappels historiques
Depuis les travaux de Kaluza, Klein et même EinsteinEinstein dans les années 20/30, l'idée d'ajouter des dimensions spatiales supplémentaires ne cesse de hanter la physique. En fait, tout est parti de la découverte d'Einstein au sujet de la physique de la force gravitationnelleforce gravitationnelle. On sait qu'afin de rendre compatible la théorie de la gravitation avec sa théorie de la relativité restreinte, il avait été conduit à utiliser la théorie de l'espace-temps de Minkowski, mais en la généralisant, pour rendre celui-ci dynamique et susceptible de courbure.
Les succès de sa théorie sont impressionnants mais Einstein lui-même ne se laissait pas intimider, il savait que ce n'était qu'un préliminaire. Pour lui, la structure physique de l'Univers devait avoir la beauté et la pureté d'un temple grec. La situation restait donc détestable car, d'une part, les particules de matière comme l'électronélectron et le protonproton étaient des hypothèses additionnelles à sa théorie des équationséquations du champ de la gravitation (on ne pouvait pas les déduire de celles-ci), d'autre part, le champ électromagnétiquechamp électromagnétique lui-même ne semblait pas une manifestation de la géométrie de l'espace-temps.
Il devait nécessairement exister, à un niveau plus fondamental, un seul système d'équations de champ aux dérivées partielles, non linéaires, gouvernant une géométrie de l'espace-temps généralisée au-delà de la géométrie de Riemann. Dans un tel cadre théorique, les particules chargées intervenant dans les équations de Maxwelléquations de Maxwell du champ électromagnétique étaient des solutions, sous forme de paquetspaquets d'énergieénergie particulièrement concentrés, d'une théorie unitaire liantliant les interactions gravitationnelles et électromagnétiques.
Que fallait-il faire pour arriver à ce but ?
Une des idées les plus prometteuses est venue assez rapidement de Théodore Kaluza, et ce, dès 1919. Lorsqu'on écrit l'équation de mouvementmouvement d'une particule chargée se déplaçant dans un espace-temps courbé, il est facile de remarquer (p 212 et suivante) qu'on peut faire fusionner les termes décrivant la force de gravitation et la force électromagnétique en ajoutant une cinquième dimension spatiale à l'espace-temps. La voie est alors toute tracée, il suffirait de prendre les équations de la relativité généralerelativité générale et de les écrire dans un espace-temps à 5 dimensions.
Ce programme s'est alors heurté à plusieurs difficultés assez rapidement.
D'abord, pourquoi ne voit-on pas la cinquième dimension ? Quelques années plus tard Oscar Klein répondra Parce qu'elle est compactifiée ! ». En effet, en refermant cette dernière selon un cercle microscopique et partant dans la direction orthogonale à l'espace-temps quadridimensionnel, en chacun de ses points, elle devient trop petite pour qu'un objet macroscopique puisse y entrer. On appelle maintenant ce genre de théorie une théorie de type Kaluza-Klein.
Malheureusement, dans ce cadre, une cinquième force inconnue émerge automatiquement sous forme d'un champ scalaire que l'on n'observe pas. On peut se débarrasser des conséquences phénoménologiques désagréables d'un tel champ mais à vrai dire de façon un peu ad hoc.
L'autre problème est bien sûr, qu'entre-temps, la mécanique quantiquemécanique quantique s'était développée.
Quel rôle le quantum d’action allait-il avoir ?
En fait, bien qu'il soulève des problèmes, comme ceux de l'apparition d'infinis non renormalisables, il se trouve que c'est une bénédiction, car la dimension spatiale ajoutée étant microscopique, une particule de matière quantique voit sa composante de quantité de mouvementquantité de mouvement devenir un multiple d'un nombre entier. La conséquence incroyable est alors que la conservation de la quantité de mouvement, le long de la cinquième dimension, est juste celle de la conservation de la charge électrique !
Arrivé à ce point, les choses se compliquent encore, car c'est maintenant les forces nucléaires fortes et faibles qui font leur apparition en étant découvertes dans les années 30. En l'absence de prédictions testables, et devant des problèmes insolubles que soulevaient déjà les théories de Kaluza-Klein, les physiciensphysiciens désertent massivement le champ de recherche de l'unification pour se consacrer à la physique nucléaire et à la théorie quantique des champs, avec les succès que l'on connaît. Tous sauf Einstein, et une poignée de mathématiciensmathématiciens et de physiciens théoriciens d'envergures comme John Wheeler et Bryce DeWitt. Ce dernier, grand pionnier de la théorie quantique du champ de gravitation, est d'ailleurs un des premiers à introduire plus d'une dimension spatiale supplémentaire. Il explique en effet, qu'en rajoutant des dimensions compactifiées, sous forme de sphères ou de tores par exemple, les symétries spatiales de ces objets se traduisent simplement par les lois de conservation des particules élémentairesparticules élémentaires des champs quantiques des forces nucléaires. En fait, ces symétries correspondent précisément aux symétries de jauge des champs de Yang Mills !
Au début des années 70, les théoriciens des interactions fortesinteractions fortes des hadronshadrons explorant les conséquences étonnantes de l'amplitude de Veneziano tombent sur deux os. La théorie n'est cohérente que si l'on écrit ses équations dans un espace-temps à 26 dimensions et elle prédit deux particules bizarres que l'on n'observe apparemment pas dans les réactions nucléairesréactions nucléaires: une particule décrite par un champ scalaire et une autre par un champ tensoriel de rang deux, comme celui du champ de gravitation de Kaluza-Klein.
Joël Scherk et Yoneya sautent sur l'occasion. Ils expliquent que la théorie de Veneziano, devenue la théorie des cordesthéorie des cordes entre les mains de Susskind et Nambu, ne parle pas seulement des forces nucléaires fortes, elle doit aussi être la clé d'une unification de la physique en fournissant une théorie quantique des théories de type Kaluza-Klein !
Depuis lors, malgré 35 années de recherches intensives mélangeant mathématiques avancées et physique, riches en percées conceptuelles et révolutions théoriques, le programme d'Einstein n'est toujours pas réalisé. Dans l'état actuel, ce qui se fait de mieux est la fameuse théorie Mthéorie M où 11 dimensions sont considérées, 10 d'espace et 1 de temps.
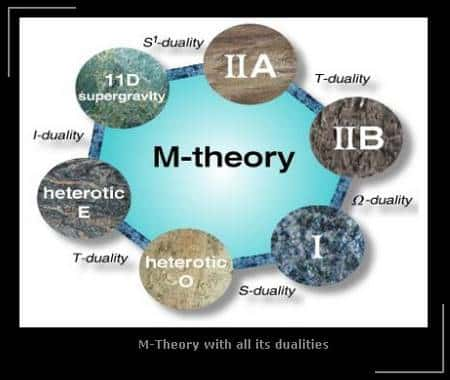
Les 5 théories des cordes en 10 dimensions et la supergravité en 11 dimensions sont les formes que prend la mystérieuse théorie M à basse énergie.
Il manque visiblement un ingrédient, même si des outils théoriques aussi puissants que les Dp-branes de Polchinski et les équations de Seiberg-Witten ont permit d'unifier les 5 théories des cordes existantes à l'aide d'un réseau de ce qu'on appelle des transformations de dualités, et de comprendre l'origine de l'entropieentropie des trous noirstrous noirs grâce aux travaux de Andrew Strominger et Cumrun Vafa de l'Université de Harvard.

Edward Witten et Joseph Polchinski en pleine discussion.
C'est là qu'Itzhak BarsBars de l'University of SouthernSouthern California entre en scène. C'est un physicien théoricien respecté dont les publications sur l'unification des interactions, la théorie des cordes, les torseurs de Penrose sont nombreuses et font autorité.
Depuis 1996, il suspecte qu'un des derniers ingrédients ne serait autre qu'une deuxième dimension temporelle compactifiée. De fait, à peu près en même temps, Cumrun Vafa avait fait remarquer qu'une des 5 théories des cordes possibles unifiées aux autres par la théorie M, la théorie mère (Mother en anglais), ne l'était que de façon assez artificielle, alors qu'en ajoutant une dimension temporelle de plus les choses se passaient beaucoup mieux. Edward Witten, le pape de la théorie M (qu'il venait d'introduire), reste quant à lui assez dubitatif devant la théorie F (Father donc père en anglais) de Vafa. Pour lui ce n'est qu'une astuce mathématique sans plus, et s'il se trompait ?

Cumrun Vafa, le père de la théorie F dans son bureau à Harvard (Crédit : Lubos Motl).
Au cours de ses recherches sur les symétries des équations des théories des cordes, de Grande Unification et de supergravitésupergravité, Itzhak Bars avait été conduit à examiner une symétrie bien particulière. Lorsque l'on considère en mécanique quantique l'ensemble des variables de position et de quantité de mouvement
d'une particule, celles-ci doivent être remplacées par des objets mathématiques que l'on appelle des opérateurs. Il y alors une condition fondamentale qui transforme les équations classiques du mouvement d'une particule en leurs correspondants quantiques en utilisant la formulation en terme d'opérateurs. Pour simplifier, on va garder la même notation pour ces nouveaux objets mathématiques en mécanique quantique. Les variables de position et d'impulsion permettent alors d'écrire cette condition fondamentale sous la forme :
[Xn, Pm] =XnPm - PmXn = i h deltadeltanm
On peut montrer que les équations de mouvement possèdent une invariance si l'on change X en P et inversement mais de la même façon en tous points de l'espace et du temps où se trouvent la particule. Or, les équations de la physique des interactions fondamentales sont basées sur des symétries de transformations appliquées, non pas globalement dans l'espace, mais localement. Ce sont les fameuses symétries dites de jauge basées sur des groupes de Lie.
Que se passerait-il si cette symétrie globale entre position et impulsion devenait locale ?
Dans ces conditions, positions et impulsions deviendraient fondamentalement impossibles à distinguer dans les équations en chaque point de l'espace. Quelque chose de stupéfiant a commencé à émerger des calculs de Itzhak Bars, cette symétrie locale n'était possible que si l'on rajoutait une dimension spatiale de plus et une dimension de temps supplémentaire ! En outre, plusieurs équations décrivant le mouvement de différentes particules, dans des espaces-temps de dimensions et de géométries différentes, devenaient alors des cas particuliers d'une équation plus générale.
Itzhak Bars a alors écrit des équations similaires à celles du modèle standardmodèle standard, mais dans un espace-temps à 4 dimensions spatiales et deux dimensions de temps. En terme technique, il a écrit un LagrangienLagrangien avec les mêmes groupes de jauge que ceux du modèle standard, SU(3)*SU(2)*U(1), mais comportant des champs de neutrinosneutrinos aussi bien droits que gauches (alors que seuls des neutrinos gauche apparaissent dans le modèle standard), un champ de Higgs dont la massemasse n'est pas donnée et un champ scalaire. En compactifiant à la façon des théories de Kaluza-Klein pour retomber sur 3 dimensions d'espace et une de temps, il a obtenu les résultats suivants :
- le terme du Lagrangien de chromodynamique quantiquechromodynamique quantique responsable d'une violation CPviolation CP non observée est automatiquement exclu. Il n'est plus nécessaire de « tuer » ce terme de façon ad hoc en introduisant une nouvelle particule inobservée, l'axionaxion ;
- la masse du Higgs et surtout la brisure de symétrie du modèle électrofaible, que l'on devrait observer avec le LHCLHC, sont sous contrôle d'un champ scalaire que l'on peut identifier au fameux dilaton de la théorie des cordes. C'est important car potentiellement, si la théorie des cordes est exacte, on aurait des prédictions testables à basses énergies de cette théorie ;
- des neutrinos droits existeraient mais ils ne se coupleraient que faiblement par l'intermédiaire du Higgs avec les autres particules. Ils pourraient donc être des candidats pour la matière noirematière noire.
De telles prédictions persisteraient dans le cadre de la théorie M et de la plus spéculative encore théorie F. Sauf qu'on passerait alors à un espace-temps à 13 dimensions, 11 spatiales et 2 de temps. Le sceptique pourra dire que cela commence à faire vraiment beaucoup d'épicycles, et il aura peut être raison. De plus, l'introduction de deux dimensions de temps peut conduire à des paradoxes avec la causalité dont certains pourraient être fatals à la théorie. Il y aussi des problèmes potentiels avec la mécanique quantique et la réduction du paquet d'ondes. Difficile de dire si l'on a affaire à une simple astuce de calcul, comme l'emploi de fonctions complexes en théorie des ondes classiques, d'une dimension spatiale supplémentaire en géométrie projective, ou si deux dimensions temporelles font vraiment partie de notre Univers. Il est en tout cas certain qu'en explorant cette voie, des propriétés cachées des équations de la physique dans un espace-temps plus 'conventionnel' pourront être mises en évidence.























