au sommaire

Ernst Ising, le physicien à l'origine d'un célèbre modèle décrivant les matériaux magnétiques. Crédit : th.physik.uni-frankfurt.de
La physique de la matière condensée n'est pas aussi médiatique que la physique des particules élémentaires. Pourtant, il existe bien des liens entre la plus célèbre théorie de la physique des hautes énergies, la théorie des supercordes, et la physique des transitions de phasestransitions de phases, décrivant par exemple le passage de la glace à l'eau liquideliquide ou encore l'apparition d'un état supraconducteursupraconducteur.
Certains des outils mathématiques et même certains concepts physiques sont employés dans les deux domaines et plusieurs des théoriciens des supercordes ont réalisé des travaux importants en physique de la matière condensée. On peut citer par exemple les cas de Curtis Callan et Alexander Polyakov.
L'essentiel des outils mathématiques partagés entre ces deux disciplines repose sur la notion de champ conforme mais certains suspectaient un autre lien, à nouveau purement mathématique. Il s'agirait d'un groupe de Lie, l'un de ces fameux groupes de symétries que l'on retrouve dans toute la physique des particules, et pas l'un des moindres puisqu'il s'agit de E8. Ce groupe a été fortement médiatisé ces dernières années, notamment grâce aux travaux de l'équipe du projet de l'Atlas of Lie Groups and Representations.
Utilisé pour décrire l'unification des particules élémentaire médiatrices des forces à l'aide de la théorie hétérotique des supercordes, ce groupe devait intervenir pour comprendre l'apparition de certaines pseudoparticules, analogues aux phononsphonons, dans certains matériaux magnétiques.
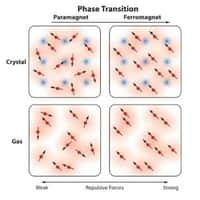
On peut comprendre le comportement des matériaux magnétiques à partir de théories généralisant un modèle proposé dans les années 1920 par Ernst Ising dans sa thèse. Il s'agit d'un modèle simple dans lequel on peut considérer des particules sur une ligne qui serait horizontale comme des petits aimantsaimants dont l'aimantationaimantation serait toujours verticale. On fait en fait intervenir la notion de spinspin avec deux états possibles, « haut » et « bas ». Comme deux aimants, ces particules sont en interaction magnétique mais on suppose que chaque particule n'est sensible qu'à l'influence de ses deux voisines.
La question que s'était posée Ising était de savoir si une aimantation spontanée pouvait se produire avec une majorité de spins orientés dans une seule direction. Sa réponse fut négative dans le cas à une dimension et il pensait qu'il devait en être de même pour un objet en 3 dimensions comme un cristal dont les atomesatomes se comporteraient de façon similaire. Il se trompait.
Alors qu'il avait abandonné la recherche pour se consacrer à l'enseignement, il ignora pendant des dizaines d'années que son modèle avait attiré l'attention de Heisenberg dans ses propres tentatives pour expliquer le ferromagnétismeferromagnétisme des aimants et que des théoriciens comme Rudolph Peierls et surtout Lars Onsager avaient étendu ses calculs au cas à deux dimensions. A la fin des années 1940 et au début des années 1950, Onsager et Chen Ning Yang concluaient qu'une transition de phase expliquant la magnétisation spontanée au-dessous de la température de Curie d'un aimant apparaissait effectivement dans un model d'Ising à deux dimensions. Depuis lors, on ne compte plus le nombre d'articles publiés utilisant le modèle de Ising pour décrire des phénomènes de transition de phase en physique statistique.
Il ne s'agissait encore que d'une transition de phase dite classique mais depuis quelque temps, les physiciensphysiciens se sont rendu compte qu'il existait aussi des transitions de phase dites quantiques.
Si l'on considère un modèle simple d'atomes dans un cristal à une température en dessous de son point de fusionfusion, l'agitation thermique de ces atomes peut se comprendre comme des mouvementsmouvements d'oscillations désordonnées autour des sites où se trouvent ces atomes. L'ensemble constitue tout de même une phase encore ordonnée sous forme d'un réseau. Les oscillations des atomes font intervenir des fréquencesfréquences déterminées par les caractéristiques des atomes et du réseau cristallinréseau cristallin du solidesolide. Au-dessus de la température de fusion, les fluctuations thermiques sont si importantes que le solide fond.
Dans le cas de la physique classique, lorsqu'on refroidit un tel solide en faisant tendre sa température vers le zéro absoluzéro absolu, les mouvements d'oscillations des atomes doivent se figer jusqu'à atteindre théoriquement l'immobilité absolue à 0 kelvinkelvin. Dans le cadre de la mécanique quantiquemécanique quantique, une telle immobilité est impossible en raison des inégalités de Heisenberginégalités de Heisenberg qui interdisent une immobilité et une localisation parfaites des particules. Il doit exister des fluctuations quantiques associées à une énergie dite du point zéro pour un oscillateur quantique et la fréquence des oscillations du point zéro doit être reliée aux caractéristiques du réseau cristallin.
Au zéro absolu, les fluctuations quantiques prennent le dessus sur les fluctuations thermiques. La nature de ces fluctuations dépend des paramètres en liaison avec le réseau cristallin que l'on peut modifier de l'extérieur, par exemple en comprimant le solide. Les calculs indiquent que, tout comme les fluctuations thermiques peuvent devenir arbitrairement grandes à une température critiquetempérature critique et provoquer un changement de phase, d'autres phases quantiques pour un système au zéro absolu peuvent apparaître en modifiant certains des paramètres du système considéré. On parle alors de transitions de phases quantiques.
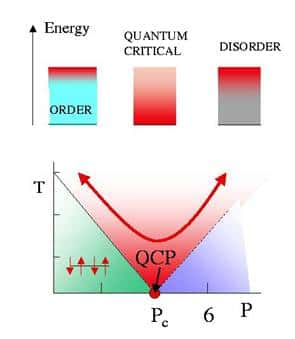
Ce schéma illustre certaines caractéristiques d'une transition de phase quantique avec un point critique quantique. Le paramètre P décrit un état ordonné dans un système, par exemple une alternance régulière de spin haut et bas à gauche qui apparaît à basse température T dans un matériau magnétique. Le point critique quantique QPC au zéro absolu indique la supperposition des états d'ordre et de désordre pour le système. Crédit : www.physics.rutgers.edu
Lorsqu'un solide fond, son état passe de l'ordre au désordre et on peut relier l'importance de l'état d'ordre de ce solide à un paramètre. Lors d'autres transitions de phases on peut obtenir une situation analogue. Toujours d'après les calculs, il existe un point critique quantique à température nulle ou un système est dans une superposition quantique d'état d'ordre et de désordre. On connaît dans le cas des transitions de phases classique un cas similaire où on n'est en présence ni vraiment d'un liquide ni vraiment d'un gazgaz mais dans le cas quantique la situation ressemble plus au cas du chat de Schrödingerchat de Schrödinger.
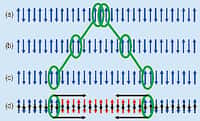
C'est en considérant un modèle de Ising dans un état correspondant à celui d'un point critique quantique que des physiciens comme Alexander Zamolodchikov avaient prédit l'émergenceémergence de pseudoparticules analogues aux phonons des solides décrits par le groupe de Lie E8.
L'émergence de pseudoparticules dans un modèle de Ising qui est une chaîne de spins n'est en soi pas nouvelle et est même bien connue. En revanche, étudier ce phénomène à 0 K fait intervenir des phénomènes nouveaux. Dans le cas considéré par Zamolodchikov, on a une chaîne de spins orientés haut et bas que l'on plonge dans un champ magnétiquechamp magnétique perpendiculaire à ces orientations. Cela va favoriser un basculement des spins qui, s'influençant magnétiquement, vont provoquer la propagation d'autres basculements, un peu à la façon d'une onde se déplaçant sur une corde. Les règles de la mécanique quantique impose alors l'existence d'un quantum d'énergie, une pseudoparticule, associé à cette onde.
Bien sûr, le zéro absolu étant une limite inatteignable, on pourrait croire que la notion de transitions de phase et de point critique quantiques n'est qu'un artefact purement mathématique sans véritable conséquence physique. De façon surprenante, il n'en est rien et la possibilité pour un système d'exhiber ces phénomènes à 0 K a des conséquences observables à des températures supérieures. On suspecte par exemple que cela a à voir avec les supraconducteur à hautes températures critiques.
Remarquablement, les calculs de Zamolodchikov montrent que 8 pseudoparticules d'énergies différentes décrist par le groupe E8 doivent apparaître et que le rapport des énergies des deux premières particules doit être donné par un nombre bien connu depuis l'antiquité : le nombre d’or.
Récemment, Radu Coldea de l'Université d'Oxford et ses collègues du Rutherford Appleton Laboratory et du Helmholtz Zentrum Berlin (HZB) ont réalisé l'équivalent de l'expérience de pensée de Zamolodchikov en plongeant du niobate de cobaltcobalt refroidis à 40 mK dans un champ magnétique. En bombardant ce matériaumatériau par un flux de neutronsneutrons, il est simultanément possible de provoquer l'apparition des quasi-particules prédites par Zamolodchikov et de mesurer leurs énergies.
Comme il l'explique dans un article de Science, lorsque la valeur critique de 5,5 teslasteslas a été approchée, les physiciens ont effectivement découvert l'apparition de deux quasi-particules avec les énergies prédites par la théorie. Malheureusement, il n'a pas encore été possible de vérifier toutes ces prédictions et d'observer tout le spectrespectre de particules découlant de l'apparition de la symétrie E8 pour les états d'énergies des quasi-particules.