au sommaire
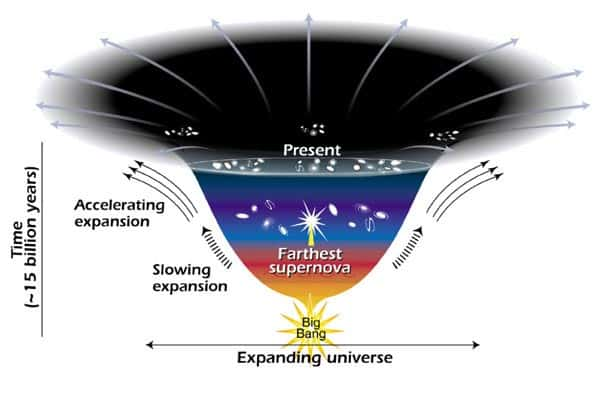
L'expansion de l'Univers depuis le Big Bang et sa phase d'accélération actuelle (Crédit : NASA).
Brian Greene, l'un des théoriciens des supercordes les plus réputés, et bien connu du grand public pour son ouvrage "L'Univers élégant", vient de faire avec sa collègue Janna Levin une proposition intéressante pour expliquer à la fois l'expansion accélérée de l'Univers et la stabilité des dimensions spatiales supplémentaires que l'on utilise dans les théories de Kaluza-Klein, et surtout, en théorie des cordes. En étudiant un modèle simple capturant l'essentiel du problème physique que l'on cherche à résoudre, les théoriciens parlent de "modèle jouet" (Toy model en anglais), ils viennent de trouver une alternative au mécanisme de Bousso-Polchinski utilisant des membranes. Ils font pour cela intervenir un phénomène célèbre en physique, l'effet Casimir. Celui-ci est d'ailleurs étroitement connecté à la notion d'énergie exotiqueexotique, que l'on fait intervenir dans les équations pour stabiliser là aussi les trous de vers et empêcher qu'ils ne se fermentferment en interdisant tout voyage à la "Stargate". Surprise ! Ce mécanisme de stabilisation génère alors aussi un modèle cosmologique avec expansion accélérée.

Brian Greene (Crédit : NOVA).
Comprendre ce que Briane Greene et Janna Levin ont fait n'est pas aussi difficile qu'on pourrait le croire, même si cela nécessite un peu de travail. Cet article se propose donc de mener le lecteur à travers une petite "excursion en montagne". Il y aura quelques équations mais que personne ne s'effraie, il n'y aura pas besoin de maîtriser la physique ou les mathématiques qui tournent autour pour les comprendre, de même qu'il n'y a pas besoin de savoir peindre comme Michel-AngeAnge pour analyser et comprendre une de ses peintures. Elles ne seront là que pour faire passer des idées et donner un aperçu de l'Univers des physiciensphysiciens théoriciens.
On ne dissimulera pas quand même le fait que la consultation des dossiers de Futura-Sciences sur la relativité générale et la théorie des trous de vers pourrait bien être nécessaire pour certains. En outre, ces dossiers possèdent des liens permettant d'approfondir bien des points sur la relativité généralerelativité générale.
Le contexte : Les théories de Kaluza-Klein

Theodor Kaluza.
Pour bien comprendre les problèmes auxquels les physiciens ont été confrontés, il faut remonter aux premières tentatives de théorie unitaire, celles d'EinsteinEinstein et Kaluza-Klein. Dans le cadre de la théorie de Kaluza-Klein, en étendant le nombre de dimensions spatiales de l'espace, on arrive à donner une interprétation géométrique de toutes les forces, et pas seulement de la gravitationgravitation, à partir de la géométrie/topologie de l'espace-tempsespace-temps.
Si l'on considère les équations d'Einstein reliant la courbure de l'espace-temps à une distribution d'énergie et d'impulsion, elles s'écriront, dans le cas où la source du champ de gravitation est un champ électromagnétiquechamp électromagnétique, sous la forme suivante :
Le membre de gauche fait intervenir la géométrie de l'espace-temps. Il est construit à partir des dérivées spatiales et temporelles de la métrique de cet espace-temps.
Le membre de droite fait lui intervenir ce qu'on appelle le tenseurtenseur impulsion-énergie des sources du champ de gravitation. Ici, il s'agit d'un champ électromagnétique (em) pur. Dans le vide, les équations précédentes se réduiraient à l'équation donnée par l'annulation du tenseur de courbure contracté dit tenseur de Ricci :
La magie de la théorie de Kaluza-Klein est, qu'en écrivant cette dernière équation pour un espace-temps à 5 dimensions avec une dimension d'espace supplémentaire compactifiée sous forme de cercle, on retombe sur les équations du champ de gravitation en 4 dimensions couplées à un champ électromagnétique gouverné par les équations de Maxwelléquations de Maxwell !
C'est à dire que l'on a les équations ci dessous :
Le processus peut être généralisé, en ajoutant à notre espace-temps macroscopique à 4 dimensions des espaces géométriques microscopiques "internes" à m dimensions pour chaque point de cet espace, comme on le verra un peu plus en détails plus loin. Ces dimensions supplémentaires doivent être compactifiées et de très petites tailles pour être compatibles avec le fait qu'on ne détecte pas ordinairement des dimensions spatiales de plus dans lesquelles les atomesatomes pourraient se déplacer.
Les symétries géométriques des dimensions supplémentaires donnent alors les types de groupes de jauges associés aux forces et aux particules. Ce sont des groupes de Lie dont l'importance en physique et en mathématique ne saurait être sous-estimée.
Ainsi, selon une dimension supplémentaire donnant un cercle, la conservation de l'impulsion d'une particule le long de cette dimension compacte découle de l'invariance par rotation des équations selon ce cercle. Il se trouve que cette loi de conservation en 5 dimensions se traduit par la loi de conservation de la charge électrique en 4 dimensions associée au groupe de Lie U(1) des équations de Maxwell.
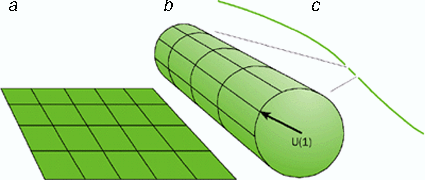
Une surface enroulée et compactifiée sous forme d'un cylindre ressemble de loin à un objet à une dimension, une ligne. Le groupe de rotation déplaçant un point d'un cercle en un autre est le groupe de Lie U(1) (Crédit : physicsweb).
Si on avait une n sphère on en sortirait SU(2), SU(3) etc...et donc, à chaque fois, la conservation des charges de QEDQED, QCDQCD etc...c'est juste la conservation de l'impulsion en dimensions supplémentaires! Ces charges donnent aussi la valeur de la constante de couplage de ces interactions en liaison avec la géométrie et la taille des dimensions supplémentaires.
Merveilleusement simple, élégant et économique
Maintenant, on sait que l'équation de Schrödingeréquation de Schrödinger pour une particule confinée dans une boîte donne pour celle-ci des niveaux d'énergies en fonction de la taille et de la forme de la boîte. Si on écrit une telle équation pour une particule relativiste (Klein Gordon en fait) à 4+n dimensions, une partie de la fonction d'onde est confinée dans les dimensions supplémentaires. En conséquence, il apparaît un spectrespectre discret d'énergie qui par E=mc2 donne des massesmasses en 4D à des particules initialement sans masse en 4+n dimensions.
On peut voir un aperçu plus précis de ce mécanisme à l'aide des équations suivantes.
Commençons par Klein-Gordon en 4 dimensions sans masse (on pose c=1).
Maintenant passons à KGKG en 5 dimensions avec une dimension supplémentaire compactifiée selon un cercle de rayon R et paramétrisée par la coordonnée s
On peut alors, en raison de la périodicité et de la compacité de la dimension supplémentaire, décomposer le champ en série de Fourier discrète. On obtient alors comme solution (le n ne correspond pas aux dimensions de l'espace ici):
qui une fois reportée dans l'équation précédente nous donnera une série d'équations sous la forme:
Cela constitue des équations de KG avec masse Mn pour différentes particules !
Ce mécanisme est très général et il s'applique aux autres équations décrivant les champs de particules de la physique.
En résumé : les quarksquarks, les électronsélectrons, les photonsphotons, les neutrinosneutrinos et les gluonsgluons avec leurs masses et leurs constantes de couplages/charges, ce ne serait que de la relativité générale plus de la mécanique quantiquemécanique quantique en 4+n dimensions.
Malheureusement, dans leurs formes initiales, les théories de types Kaluza-Klein souffrent de nombreux problèmes (non renormalisation, absence de spectre chiral des particules etc...). Bien que reposant elles aussi sur des dimensions supplémentaires, les théories des cordes soit résolvent les problèmes précédents, soit donnent de meilleures perspectives de les surmonter.
La cosmologie selon Kaluza-Klein
Passons maintenant à la cosmologiecosmologie de KK et imaginons un modèle simple de l'Univers où l'espace-temps est plat et en deux dimensions spatiales. Les équations d'Einstein permettent de construire un modèle de type Big BangBig Bang très semblable à celui que l'on a avec 3 dimensions d'espace plus une de temps et une géométrie plate. L'intervalle d'espace-temps en coordonnées cartésiennes est alors donné par l'équation ci-dessous:
Le facteur a(t) dépendant du temps est tout simplement le facteur responsable de la dilatationdilatation des distances spatiales au cours du temps, et il représente donc l'expansion de notre Univers en 3 dimensions. Cette solution des équations d'Einstein est obtenue lorsqu'on fait l'hypothèse que la distribution de matièrematière et d'énergie est homogène et isotropeisotrope.
En quatre dimensions, si l'on introduisait une densité de matière sous forme d'un fluide, et avec une pressionpression
qui pourrait être reliée à une densité d'énergie du vide, alors la dérivée seconde par rapport au temps du facteur d'expansion a(t), et que l'on écrit comme d'habitude avec deux points au-dessus de la lettre a, vérifiera la relation suivante :
Clairement, cette dérivée seconde du facteur d'expansion représentera une accélération ou une décélération en fonction du signe de la somme présent dans le second membre.
Prenons maintenant notre Univers plat en 2D et supposons qu'il soit l'analogue d'une feuille avec une largeur et une longueur. Commençons, comme précédemment, par enrouler la feuille pour en faire un cylindre puis refermons notre cylindre pour en faire un pneupneu. Mathématiquement, l'objet que l'on obtient est un tore et la géométrie à sa surface reste plane. On a toujours affaire à la géométrie d'EuclideEuclide, ce qui ne serait pas le cas sur une sphère.
Ce tore est caractérisé par deux rayons correspondant aux deux cercles le formant. On peut en effet générer une telle surface en prenant un petit cercle centré sur un grand et en déplaçant le long de celui-ci ce petit cercle.
Le modèle d'Univers que l'on vient de réaliser est un autre modèle jouet. Il reste homogène mais cette fois il est anisotropeanisotrope, car en se déplaçant dans une de ses direction on ne revient pas à son point de départpoint de départ en parcourant la même distance, ce qui serait le cas sur une sphère par exemple.
Tout naturellement, on peut obtenir là aussi un Univers en expansion. Mais rien ne nous oblige à avoir le même rythme d'expansion selon les deux cercles caractérisant notre Univers-tore. On aura donc deux facteurs d'expansion a(t) et b(t) et une métrique d'espace-temps qui s'écrira :
De la même façon que l'on construit un espace à trois dimensions en prenant une dimension supplémentaire orthogonale à un plan, on peut construire un espace à plus de trois dimensions en rajoutant des dimensions supplémentaires orthogonales à ce plan. Un processus simple et général de constructionconstruction d'espace à plusieurs dimensions peut être vu de la façon suivante : on prend un espace à n dimensions et on ajoute une dimension orthogonale aux autres et on répéte le processus avec l'espace à n+1 dimensions obtenu.
Ces espaces peuvent avoir des formes très compliquées, comme des "tores" à deux dimensions mais plusieurs "trous", ou encore être des multi-tores construits non plus avec deux cercles mais m cercles. Le premier cas est représenté par le schéma ci-dessous où l'on imagine que l'on obtient un espace à 4 dimensions en rajoutant à chaque point d'un plan deux directions orthogonales supplémentaires mais refermées sur elle-même pour faire un tore dit de genre 3 puisque possédant trois trous. Le nombre de trous d'un tore, son genre, sert à classifier ce type de surface. On parle alors de topologies différentes car aucune transformation continue ne permet de passer de l'une de ces surfaces à l'autre par déformation.
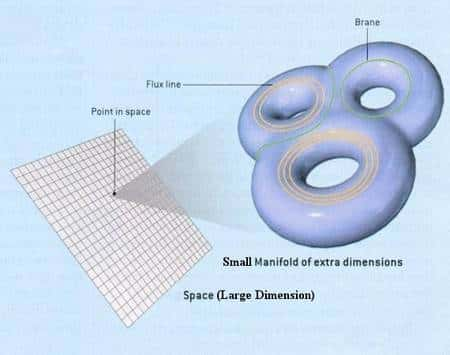
Crédit : http://universe-review.ca/
Dans le cas d'un multi-tore, que l'on peut obtenir en 3 dimensions en collant non plus les côtés opposés d'une feuille mais les faces opposées d'un cube, on aura donc un autre modèle d'Univers homogène mais anisotrope avec cette fois trois facteurs d'expansion (De tels Univers avec des topologies non triviales ont été considérés par Jean-Pierre Luminet et ses collègues). La règle générale pour un espace-temps de ce genre à n+1 dimensions se devine aisément. En prenant n facteurs ai dépendant du temps on aura la métrique suivante:
Brian Greene et Janna Levin ont utilisé des Univers jouets de ce genre dont un multi-tore où toutes les dimensions sont multipliées par un même facteur de dilatation au cours du temps. Si l'on note dy2 l'intervalle de distance sur ce tore alors on se trouve ramené à la métrique déjà vue précédemment avec deux facteurs d'expansion.
C'est là où tout se complique !
On a en effet passé sous silence toute une série de questions qui doivent recevoir des réponses lorsqu'on cherche à bâtir une physique et une cosmologie avec des dimensions spatiales supplémentaires.
- Qu'est-ce qui fixe la taille et la forme de ces dimensions supplémentaires ?
- Pourquoi 3 des dimensions spatiales sont-elles entrées en expansion au début du Big Bang et pourquoi les autres non ?
- Si je perturbe ces dimensions supplémentaires très petites, cela va-t-il rester stable ? Cela ne va pas s'effondrer comme un trou noirtrou noir ou au contraire entrer en expansion ?
La théorie des cordes, en fait plutôt son extension qui fait intervenir en plus d'objets à une dimension comme les cordes des objets à p dimensions les membranes, offre une solution possible, comme Joseph Polchinski et Raphaël Bousso l'ont démontré avec quelques autres au début des années 2000.
En s'enroulant autour des dimensions supplémentaires comme des élastiques, et surtout en introduisant des champs dans les dimensions supplémentaires analogues à des champs magnétiqueschamps magnétiques, on peut, grâce aux membranes, stabiliser celles-ci et empêcher qu'elles ne s'effondrent ou n'entrent en expansion.

Joseph Polchinski, le découvreur de la théorie des Dp-branes en théorie des cordes et Sugumi Kanno une physicienne Japonaise lors d'un colloque (Crédit Sugumi Kanno).

Raphael Bousso, l'ancien thésard de Hawking est devennu depuis célèbre pour ses travaux sur le principe Holographique et le mécanisme de stabilisation des dimensions supplémentaires qu'il a découvert en collaboration avec Joe Polchinski (Crédit : Université de Berkeley).
Cet espace-temps à plusieurs dimensions devient alors comme un milieu élastique pouvant exister sous plusieurs formes stables (ex sphère, ellipsoïdes, réseau cristallinsréseau cristallins etc..) et donc avec des minimums d'énergies possibles plus ou moins métastablesmétastables dans d'autres cas.
Nous habiterions ainsi selon ces théories dans un des états d'énergie stables/métastables possibles de ce milieu élastique spatio-temporel, avec des courbures et des tensions particulières.
Ces niveaux d'énergies, et donc les types de forces et de particules possibles, dépendent des paramètres définissant la forme et la topologie des dimensions supplémentaires. Or, en physique, l'état d'énergie minimale des champs est aussi appelé l'énergie du vide...et il s'agirait en fait de la célèbre constante cosmologiqueconstante cosmologique que l'on peut écrire dans les équations d'Einstein sous la forme d'une constante C comme on peut le voir ci-dessous.
Si j'appelle H cette énergie du vide et qu'elle dépend de plusieurs des paramètres précédents, elle va se représenter par une surface dans l'espace des paramètres des formes des dimensions supplémentaires.
Si j'imagine un monde où les dimensions supplémentaires ne dépendent que de 2 paramètres alors je peux représenter les énergies possibles du vide et ces dimensions comme une surface de niveau dont la hauteur définit cette énergie justement. J'ai donc un "paysage" avec des vallées (les minimums stables de l'énergie du vide) et des sommets.
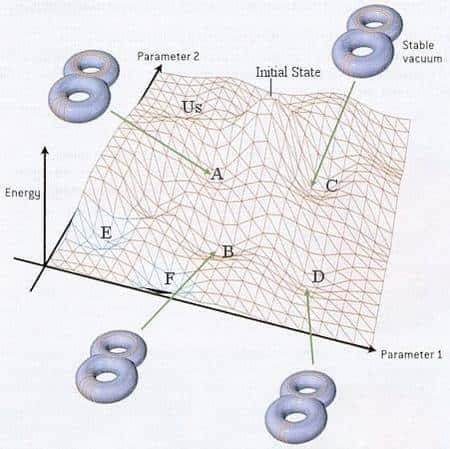
Le landscape d'un Univers jouet avec deux dimensions spatiales compactes supplémentaires enroulées sous la forme d'un tore de genre 2 et stabilisé dans différents états de taille et de forme par les modes d'enroulement des cordes/membranes et les flux "magnétiques" des champs introduits par la présence des membranes (Crédit : http://universe-review.ca/)
En anglais paysage se dit "Landscape", il y a donc toute une série d'Univers possibles donnés par différentes localisations sur le Landscape.
Nous vivons dans une des vallées/creux de ce paysage car c'est une loi de la physique qu'un système occupe un minimum d'énergie pour être stable. Eventuellement on est en train de rouler lentement d'une vallée dans une autre plus basse (vide métastable), ou de passer d'une vallée à l'autre par effet tunneleffet tunnel.
Ok, ok... mais combien y a t-il de creux ou des vallées possibles stables dans un paysage de cordes avec 10/11 dimensions ?
Dans le cas des théories de corde les plus réalistes, on compactifie les dimensions supplémentaires sous forme de figures géométriques à 6 dimensions, les espaces de Calabi-Yau. Ce sont des objets complexes qui peuvent être décrits par un grand nombre de paramètres en liaison avec leur topologie.
Au final, ils donneraient lieu à au moins 10500 vides métastables ou stables possibles!
Un nombre bien évidemment gigantesque et qui rend potentiellement très difficile, et peut être impossible, la prédiction exacte des masses et des constantes de couplages des particules du modèle standardmodèle standard.
L'expansion accélérée de l'Univers
On sait maintenant depuis 1998 que l'Univers observable, après une phase de décélération juste après le Big Bang, est en phase d'accélération depuis plusieurs milliards d'années. On le sait en raison des mesures sur les supernovaesupernovae de type SNSN Ia. La raison de cette accélération peut se comprendre si l'on revient à l'équation gouvernant le facteur d'expansion a(t) de l'Univers.
Une constante cosmologique C peut se manifester comme une sorte de pression négative ou positive. Selon son signe et son importance par rapport aux autres contributions de densité de matière, de rayonnement et aux pressions associées, l'expansion s'accélérera ou au contraire ralentira.
On pense généralement que cette constante cosmologique représente une énergie du vide et c'est pourquoi on parle d'énergie noireénergie noire, car quasi invisible directement, lorsque l'on rend compte de l'accélération de l'expansion de l'Universaccélération de l'expansion de l'Univers par cette constante.
Si l'on adopte la théorie des cordes et le mécanisme de Bousso-Polchinski alors l'énergie noire serait reliée aux dimensions supplémentaires. Mais on a vu qu'il n'est absolument pas évident de trouver un bon vide, stable et représentant aussi bien le modèle standard que le modèle cosmologique avec matière noirematière noire que nous observons. On voudrait un mécanisme avec beaucoup moins de paramètres libres et prédisant de façon beaucoup plus générique la stabilité des dimensions et l'accélération de l'expansion.
Brian Greene et Janna Levine se sont alors rappelé de l'effet Casimireffet Casimir. Une modification de l'énergie du vide dans une portion finie de l'espace se produit lorsqu'on confine une partie des champs de particules, comme c'est le cas avec l'exemple bien connu de deux plaques conductrices avec l'effet Casimir. Or, les champs sont aussi confinés lorsqu'ils se trouvent piégés dans les dimensions compactes des théories de KK. La modification de la densité d'énergie y est alors très forte.
Dans le modèle jouet que les deux physiciens ont considéré on trouve qu'effectivement, de manière presque automatique, les n dimensions compactes sont stabilisées pour certaines classes de topologie aussi bien des dimensions supplémentaires que de l'Univers en 3D, alors que les 3 autres entrent en expansion puis en expansion accélérée. De plus, l'ordre de grandeurordre de grandeur de l'énergie du vide produit par la prise en compte de l'effet Casimir dans les dimensions supplémentaires est bien celui de l'énergie noire.
A ce jour, malgré tout, le mécanisme exact à l'origine de la constante cosmologique et de l'expansion accéléré de l'Univers n'est toujours pas connu et bien des possibilités pour le destin futur de l'Univers restent ouvertes comme on peut le voir sur le schéma ci-dessous.
- La valeur de l'énergie du vide pourrait changer et devenir attractive au lieu de répulsive comme dans les modèles de supergravitésupergravité proposés par Andrei Linde et sa femme Renata Kalosh. L'Univers finirait par un big Crunchbig Crunch.
- La constante cosmologique en serait bien une et l'Univers continuerait éternellement son expansion accélérée avec des amas de galaxiesamas de galaxies contenant des étoilesétoiles mortes.
- Enfin, la valeur de l'énergie du vide pourrait devenir avec le temps tellement répulsive que même les noyaux d'atomes finiraient par être dissociés. C'est le scénario du Big RipBig Rip.
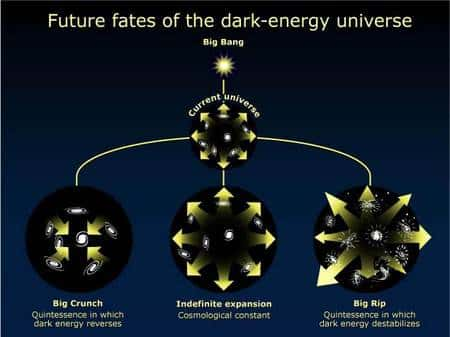
(Crédit : NASA).