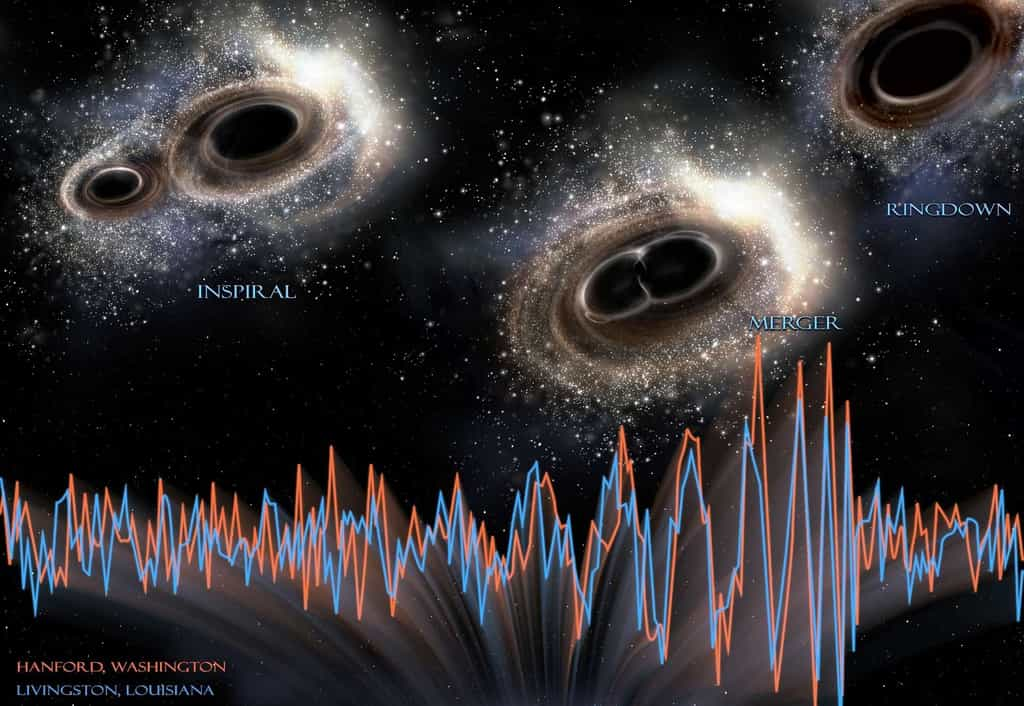
La découverte conjointe par LigoLigo et VirgoVirgo de l'émission d'une onde gravitationnelle par la source GW170817 associée à un sursaut gamma SGRB170817A, qui a, de plus, toutes les caractéristiques d'une kilonova, montre spectaculairement tout le potentiel de l'astronomie gravitationnelle. Elle confirme également que nous sommes entrés dans l'ère de l'astronomie « multimessager ».

L'évènement aurait sans aucun doute ravi le prix Nobel de physique indien Subrahmanyan ChandrasekharSubrahmanyan Chandrasekhar, qui a été un pionnier de la théorie des étoiles relativistes dans les années 1960 et de celle des trous noirs dans les années 1970. D'autant plus que l'analyse des ondes (détectées non seulement par Ligo et Virgo mais aussi par environ 70 instruments au sol ou dans l'espace dans tout le spectre des ondes électromagnétiquesondes électromagnétiques) nous assure maintenant que GW170817 était une collision d'étoiles à neutronsétoiles à neutrons mais aussi qu'au moins certains sursauts gamma courts sont bien le résultat de telles collisions qui, très vraisemblablement, forment finalement un autre objet compact, un trou noir.

L'avènement d'une nouvelle astronomie, fort justement récompensé par le prix Nobel de physique 2017, ne concerne pas seulement l'astrophysiqueastrophysique relativiste et l'astrophysique nucléaire (en éclairant l'origine des éléments lourds tels l'or et le platineplatine). Elle concerne aussi la physique fondamentale. Il y a en effet des enseignements à tirer de ce point de vue de la détection de GW170817, qui, comme son nom l'indique, s'est produit le 17 août 2017. Il en est de même avec l'annonce, le mois dernier, de la détection de GW170814 qui, remarquablement, s'est produit le 14 août 2017 ; il s'agissait cette fois d'une collision avec fusionfusion de deux trous noirs stellairestrous noirs stellaires.

Comme nous allons le voir, des évènements comme GW170817 et GW170814, dont les observations devraient se multiplier dans un avenir proche (d'autant plus qu'il est prévu d'augmenter encore la sensibilité de Ligo et Virgo), nous permettent de poser des bornes sur de la nouvelle physique, notamment sur celle que la théorie des cordesthéorie des cordes peut impliquer dans le domaine de l'existence de dimensions spatiales supplémentaires, de la nature de l'énergie noireénergie noire et d'une possible violation de l'invariance de Lorentz, invariance qui est à la base de la théorie de la relativité restreinterelativité restreinte. Commençons par discuter le cas de la collision des étoiles à neutrons.

Les ondes gravitationnelles des kilonovae, clé d'une nouvelle physique

Pour mesurer des variations dans le temps de la vitessevitesse d'expansion de l'universunivers observable, il faut mesurer les distances et les décalages spectraux de certains objets pouvant être considérés comme des chandelles standardchandelles standard, ou peu s'en faut, c'est-à-dire des objets dont la luminositéluminosité absolue est connue et relativement constante. On a de bonnes raisons de penser que c'est le cas des SNSN Ia, ces supernovaesupernovae qui sont des explosions liées à des naines blanches, puisqu'il s'agit d'objets compacts dont les massesmasses devraient être de l'ordre de la fameuse masse de Chandrasekharmasse de Chandrasekhar, ce qui limite l'énergie disponible pour le rayonnement émis, qu'il soit électromagnétique ou gravitationnel.

Si l'on utilise la métaphore du son pour décrire la propagation des ondes gravitationnellesondes gravitationnelles dans le tissu de l'espace-tempsespace-temps, ces kilonovae devraient donc être des « sirènes standard », car on peut déduire l'amplitude des ondes gravitationnelles émises à partir de leurs caractéristiques observées, tout comme dans le cas de la fusion des trous noirs. Le rapport entre l'amplitude émise et l'amplitude observée nous permet alors d'en déduire une distance, comme avec les SN Ia. Par analogieanalogie, plus une chandelle est loin, moins elle nous apparaît lumineuse ; plus une sirène est loin, moins elle nous semble puissante. 

Or, les mesures de distance se font en s'appuyant sur une échelle de techniques qui commence avec la mesure des parallaxesparallaxes stellaires dans la Voie lactéeVoie lactée et se poursuit avec les Céphéides extragalactiques jusqu'aux supernovae. Les erreurs propres à chaque technique s'accumulent et entachent d'incertitudes la mesure des distances dans l'univers, desquelles on peut déterminer la vitesse d'expansion du cosmoscosmos observable, ou, dit autrement, la fameuse constante de Hubbleconstante de Hubble, quand on dispose des mesures du redshiftredshift par ailleurs. 

Bernard F. Schutz est un physicien américain dont les recherches portent sur la théorie de la relativité générale d'Einstein, plus concrètement, sur la physique des ondes gravitationnelles. Il est l'un des directeurs et chef du groupe d'astrophysique de l'Institut Max Planck de physique gravitationnelle de Potsdam, en Allemagne. Il a joué un rôle clé dans la fondation de la revue numérique Living Reviews in Relativity. © N. Michalke, AEI

En 1986, le physicienphysicien Bernard F. Schutz a montré le premier que les ondes gravitationnelles émises par une collision d'étoiles à neutrons permettaient de mesurer la valeur de la constante de Hubble avec une précision de quelques pour cent. Surtout, en combinant la détection de ces ondes avec une contrepartie électromagnétique, il est possible d'obtenir cette valeur directement, c'est-à-dire sans se reposer sur l'emboîtage successif des techniques de mesure de distance. Le résultat serait donc plus robuste que celui qui a pu être obtenu avec le SDSS ou les mesures déduites des SN Ia puisqu'il s'affranchit de ces sources d'erreur. La mesure de la constante de Hubble à l'aide de l'étude de GW170817 et SGRB170817A (le sursaut gamma associé à cette onde gravitationnelle) est compatible avec les estimations précédentes, même celle déduite des mesures de PlanckPlanck, ce qui consolide le modèle cosmologique standardmodèle cosmologique standard. Comme les données vont continuer à affluer de cette façon dans un futur proche, il se peut que l'on apprenne de cette manière quelques-uns des secrets de l'énergie noire.

Par ailleurs, la théorie relativiste de la gravitationgravitation d'EinsteinEinstein, la relativité généralerelativité générale, prédit que les ondes gravitationnelles voyagent à la même vitesse que la lumièrelumière. Il existe pourtant des théories alternatives où ce n'est pas le cas (et même certaines où la vitesse des ondes électromagnétiques dans le vide n'est pas exactement celle que l'on croit du fait d'effets de gravitation quantiquegravitation quantique, par exemple ceux que la théorie des supercordesthéorie des supercordes implique). Dans le cas de GW170817 et SGRB170817A, les rayons gammarayons gamma sont arrivés environ deux secondes après les ondes gravitationnelles. Ce retard est sans doute dû aux mécanismes d'émission de ces ondes mais, comme les signaux ont voyagé sur une distance de 130 millions d'années, cela implique que la différence de vitesse est, de toute façon, extrêmement faible et inférieure à une borne donnée (la différence relative sur la vitesse de la lumièrevitesse de la lumière est inférieure au millionième de milliardième). De futures détections conjointes devraient permettre de démêler les parts des contributions des différences de temps d'émission par rapport au temps de propagation relatif, car seul ce dernier dépend de la distance.

On a pu également poser des contraintes sur la violation de l’invariance de Lorentz, violation qui se manifesterait notamment par des différences de vitesses de propagation pour les ondes électromagnétiques et gravitationnelles dans le vide selon leur énergie. Toutefois, dans le cas de GW170817, on a en fait testé des violations de l'invariance de Lorentz dites « non dispersives », c'est-à-dire celles qui ne sont pas reliées à ce genre de phénomènes de variation des vitesses en fonction de l'énergie ou, plus précisément, des fréquencesfréquences contenues dans les ondes.

Chercheur en astrophysique relativiste, Olivier Minazzoli a notamment travaillé pour la Nasa au JPL (Jet Propulsion Laboratory), à Pasadena, en Californie, aux États-Unis. © Olivier Minazzoli

La polarisation des ondes gravitationnelles des trous noirs

Tournons-nous maintenant vers la nouvelle détection de collision de trous noirs, avec l'observation de GW170814. Il n'y a pas eu de contrepartie électromagnétique à cet évènement, comme on devait s'y attendre en général avec la fusion de deux trous noirs de masses stellaires.

Mais, ce qui a rendu cette quatrième détection de fusion de trous noirs si intéressante, c'est d'abord le fait que trois interféromètresinterféromètres étaient impliqués pour la première fois. De quoi enfin localiser la source sur la voûte céleste avec une précision qui permet de rechercher avec beaucoup moins d'ambiguïté une éventuelle contrepartie électromagnétique.

En second lieu, ces trois machines permettent maintenant de poser des contraintes sur la polarisation des ondes gravitationnelles. Or, comme nous l'avait expliqué le physicien OlivierOlivier Minazzoli (voir article ci-dessous), membre de la collaboration Virgo et qui travaille au centre scientifique de Monaco et à l'Observatoire de la Côte d'Azur (OCA), la polarisation de ces ondes nous permet potentiellement d'aller au-delà de la théorie d'Einstein et peut-être même, bien que cela n'aille pas de soi, de rendre plus crédible la théorie des supercordes. Nous lui avons donc demandé de nous donner quelques explications supplémentaires.

Futura : Les collaborations Ligo et Virgo ont fait savoir que GW170814 permettait d'étudier la nature des polarisations des ondes gravitationnelles. Pourquoi ne pouvait-on pas le faire avant, uniquement avec les deux interféromètres de Ligo ?

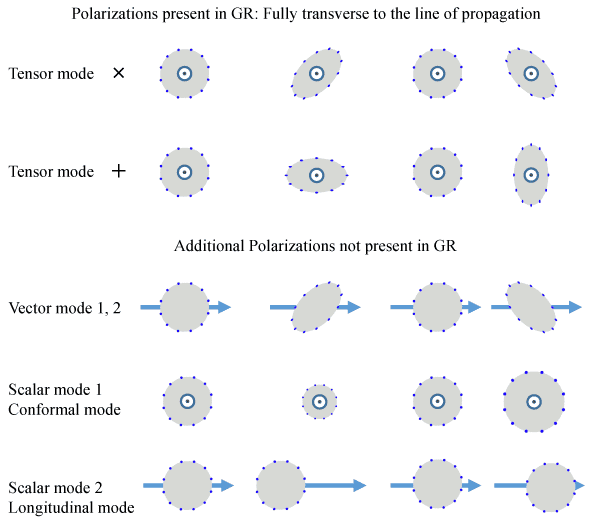
Olivier Minazzoli : Tout d'abord, rappelons que la relativité générale prédit un certain type de polarisation que l'on nomme « tensoriel ». En revanche, la quasi-totalité des théories alternatives à la théorie d'Einstein induit des types de polarisation supplémentaires, que l'on nomme « vectoriel » et « scalaire ». En tout, il y a 6 modes de polarisation théoriquement possibles, 2 pour chaque type.

Pour faire la mesure de tous les modes de polarisation envisageables théoriquement, il faut plusieurs interféromètres avec des orientations relatives différentes. Or, les deux détecteurs de Ligo sont presque coalignés. En revanche, à cause de la rotondité de la Terre, l'interféromètre de Virgo n'est pas coaligné avec ses équivalents américains. Il est donc possible de commencer à déterminer le contenu d'une onde gravitationnelle en termes de polarisation, directement depuis la mesure de celle-ci. Une première !

Néanmoins, nous ne sommes pas encore en mesure d'étudier la polarisation des ondes gravitationnelles de façon optimale. En effet, il y a 6 différents modes de polarisation théoriquement possibles et intriqués. Ainsi, pour pouvoir décorréler les effets de chacun des modes de polarisation sur les interféromètres, il faudrait idéalement avoir au moins 6 interféromètres orientés différemment, ce dont nous ne disposons pas actuellement.

Malgré tout, avec les interféromètres de Ligo et Virgo, nous pouvons déjà dire si les modes de polarisation semblent soit « complètement tensoriels », en accord avec les prédictions de la relativité générale, soit « complètement vectoriels », soit « complètement scalaires ». Néanmoins, nous ne pouvons rien dire sur les cas où ces types de polarisation seraient mélangés entre eux dans le signal, avec différentes amplitudes pour chaque mode. Or, la plupart des théories allant au-delà de la relativité d'Einstein prédisent un tel mélange. Nous sommes donc encore loin de pouvoir pleinement contraindre les théories alternatives par la mesure des modes de polarisation, mais c'est une étape majeure qui a été accomplie.

Nous attendons donc avec impatience les détecteurs japonais Kagra et indien Ligo-India, qui nous permettront d'affiner ces recherches. D'autres méthodes pourraient cependant s'affranchir de la nécessité d'avoir plus d'interféromètres. En effet, nous avons récemment montré avec des collègues de la collaboration Ligo-Virgo (voir ici), que les détecteurs Ligo et Virgo seuls pourraient mesurer le contenu en mode de polarisation du fond stochastiquestochastique d'ondes gravitationnelles - c'est-à-dire, la somme des ondes qui sont individuellement trop faibles pour être détectées directement.

D'autres collègues de la collaboration ont aussi montré une telle possibilité à partir des ondes gravitationnelles produites par certaines étoiles à neutrons en rotation rapide (voir ici). L'inconvénient de ces deux méthodes est qu'il faut accumuler des données sur (potentiellement) plusieurs années avant de pouvoir détecter ces signaux. Donc, dans tous les cas, nous avons encore quelques années devant nous avant de contraindre pleinement les théories alternatives à partir des modes de polarisation contenus dans les ondes gravitationnelles observées.

Quel a donc été le résultat de la polarisation de l'onde émise par GW170814 ?

Olivier Minazzoli : Il est conforme aux prédictions de la théorie de la relativité générale ; la polarisation semble toujours purement tensorielle, ou pour le moins largement sous cette forme. C'est déjà ce que nous disaient les études concernant les pulsarspulsars binairesbinaires. Car, si d'autres modes de polarisation étaient présents, et avec une amplitude non négligeable, la binaire perdrait de l'énergie beaucoup plus rapidement sous forme d'ondes gravitationnelles et l'on observerait donc les pulsars se rapprocher entre eux plus vite que ce que l'on constate.

Toutefois, les prédictions concernant ce phénomène varient selon les modèles utilisés et il est donc difficile d'aboutir à des conclusions indépendantes de la théorie considérée.

La grande nouveauté avec la mise en service de détecteurs comme Ligo et Virgo est que l'on peut tester la présence d'une composante non tensorielle sans avoir à faire intervenir un modèle précis de nouvelle physique. Nos conclusions deviennent alors indépendantes - ou moins dépendantes - des cadres théoriques de la physique contemporaine, ce qui est idéal pour tenter de s'affranchir de tout biais que nos connaissances actuelles pourraient introduire dans nos interprétations des phénomènes gravitationnels.

Supercordes : les ondes gravitationnelles pourraient-elles révéler leurs dimensions supplémentaires ?

Article de Laurent SaccoLaurent Sacco publié le 12/07/2017

La détection de certaines caractéristiques des ondes gravitationnelles pourraient révéler l'existence de dimensions supplémentaires, prédites par la théorie des cordes. C'est d'autant plus fascinant et excitant que les collisions de particules au LHCLHC et l'étude du rayonnement fossilerayonnement fossile nous ont, sur ce point, laissé sur notre faim. Toutefois, l'astrophysicienastrophysicien Olivier Minazzoli nous explique qu'il n'est en réalité pas simple de tirer des conclusions de la détection de ces caractéristiques.

L'annonce que l'étude des ondes gravitationnelles par des détecteurs comme aLigo et Virgo pourrait révéler l'existence des dimensions spatiales supplémentaires requise pour la cohérence de la théorie des supercordes -- ou au contraire, la réfuter -- a, pour de bonnes raisons, connu un certain succès médiatique. Mais comme l'expliquait Futura à la fin de l'article consacré à cette fascinante possibilité (voir plus bas), il faut tout de même garder la tête froide car aucune de ces deux possibilités ne va de soi. Sans vouloir dissiper tout espoir, c'est une bonne chose de regarder d'un peu plus près pourquoi il y a loin de la coupe aux lèvres.

En effet il n'est pas rare en physique et en cosmologiecosmologie que l'on soit confronté, au niveau de la précision des mesures de certains paramètres accessibles d'une théorie et des valeurs qu'elle prédit, à ce que les scientifiques appellent des dégénérescences. Ils entendent par là que deux, voire plusieurs théories peuvent parfois rendre compte des mêmes données expérimentales sans que l'on puisse les départager, au moins temporairement. À un moment donné par exemple, on pouvait rendre compte des mêmes observations en cosmologie avec différentes valeurs des quantités de matièrematière, d'énergie noire ou de courbure totale de l'univers en ajustant convenablement ces différents paramètres. Mais lorsque les mesures sont devenues plus précises et que l'on a fait entrer en jeu d'autres quantités impliquées dans le modèle cosmologique, certaines dégénérescences ont été levées, comme on dit, et il a été possible d'écarter certaines hypothèses ou, pour le moins, de les rendre moins probables.

Les théories PPN, un cadre pour tester les théories de la gravitation

Il faut savoir que la théorie de la gravitation d’Einstein repose sur plusieurs hypothèses. La première, sans aucun doute, est celle de la validité de la théorie de la relativité restreinte. Viennent ensuite l'existence d'un espace-temps courbe dont la géométrie est décrite par une « métrique » (qui permet de calculer des distances dans cet espace-temps), la validité du principe d'équivalence et, bien sûr, les équationséquations d'Einstein.

Le physicien Clifford Will est un pionnier des tests de la relativité générale ainsi que des alternatives à la théorie d'Einstein via les théories de type PPN. © University of Florida

Or, on peut contester ces hypothèses et construire des alternatives aux équations d'Einstein (rejeter la théorie de la relativité restreinte est possible mais problématique). Les physiciens ont ainsi considéré ce qu'ils appellent des théories métriques de la gravitation. L'espace-temps courbe y est conservé, ainsi que généralement aussi le principe d’équivalence, mais d'autres équations que celles d'Einstein sont considérées, ainsi que l'introduction de champs supplémentaires qui s'ajoutent à celui associé au « tenseurtenseur métrique » et qui sont des champs scalaires et vectoriels.

Théoriciens et expérimentateurs ont bien sûr cherché à départager ces théories, en considérant des solutions approchées de leurs équations, y compris de celles d'Einstein. Elles peuvent servir à calculer les mouvementsmouvements de la lumière (qu'il s'agisse d'ondes radio ou de rayons gamma) et des planètes en dehors des corps célestes mais aussi les émissions d'ondes gravitationnelles qu'ils peuvent générer. C'est ainsi que vers la fin des années 1960 (le début de cette approche remontant aux années 1920 avec Eddington), la théorie dite des approximations post-newtoniennes paramétrisées (théories PPN, en anglais) a été développée par des physiciens comme Clifford Will et Kenneth Nordtvedt.

Elle a permis d'éliminer des théories concurrentes de celle d'Einstein et de poser des contraintes sur d'autres, comme celles dites tenseur-scalaires parmi lesquelles Brans-Dicke est un célèbre exemple, et ce, dès le début des années 1970, avec l'essor des voyages interplanétaires de sondes dans le Système solaireSystème solaire puis, plus tard, avec l'étude des mouvements des pulsars binaires rayonnant des ondes gravitationnelles.

Les ondes gravitationnelles peuvent posséder différentes polarisations selon qu’elles sont décrites par les équations de la relativité générale ou des extensions de ces équations. La polarisation peut être mise en évidence par le passage des ondes gravitationnelles à travers une distribution initialement circulaire de masses. L’effet dans le temps des deux modes de polarisation (× et +) des ondes de la théorie d’Einstein est représenté en haut sur ce schéma. La direction de propagation des ondes est perpendiculaire au plan du schéma. En bas, trois autres modes sont figurés, la flèche indiquant la direction de propagation. Les modes B sont les modes scalaires de type 1. © Claudia de Rham

Des polarisations d’ondes gravitationnelles d’interprétation délicate

La théorie des cordes conduit à des modifications des équations de la théorie de la relativité d'Einstein. Certaines d'entre elles entrent dans le cadre des théories métriques mais il est possible de postuler l'existence de ces nouvelles équations sans supposer nécessairement celle de dimensions spatiales supplémentaires. Potentiellement, c'est donc un magnifique cas de dégénérescence des théories et toutes ou partie de leurs prédictions.

Comme Futura l'expliquait dans l'article ci-dessous, Lucena Gómez et David Andriot, les deux physiciens de l'Institut Max-Planck de physique gravitationnelle qui ont proposé une idée pour mettre en évidence l'existence des dimensions spatiales supplémentaires, qu'elles soient issues de la théorie des cordes ou d'une théorie de Kaluza-Klein pure, ont mis en avant le fait qu'elles conduisent à l'existence de modes de polarisations supplémentaires des ondes gravitationnelles. Il s'agit des modes Bmodes B pour Breathing modes en anglais (à ne pas confondre avec les modes B de la théorie d'Einstein qui sont recherchés dans le rayonnement fossile).

Dans quelle mesure l'observation de ces modes B serait une preuve de l'existence de ces dimensions spatiales supplémentaires et leur non-observation une réfutation de leur existence et donc de la théorie des cordes ? C'est ce que l'on aimerait bien savoir et c'est la question que Futura a posée à Olivier Minazzoli qui travaille justement sur les tests des alternatives possibles à la théorie d'Einstein, au Centre Scientifique de Monaco et à l'observatoire de la Côte d'Azur (OCA). Il est l'un des éditeurs de la partie de Scholarpedia traitant en ligne de l'astrophysique et de la cosmologie relativiste. Voici la réponse du physicien.

« Toutes les théories alternatives vont générer plus ou moins des modes de polarisation autres que les modes × et + de la relativité générale. En particulier, les modes B (breathing) se retrouvent quasiment partout. Donc leur détection ne serait pas en soi une preuve de l'existence de dimensions spatiales supplémentaires. Par ailleurs, comme Lucena Gómez et David Andriot le mentionnent dans leur article, il n'est pas possible de prédire l'amplitude de ces modes dans le cadre général des théories avec des dimensions supplémentaires.

Leur non-détection ne permettrait donc pas non plus d'invalider l'hypothèse de l'existence de ces dimensions supplémentaires et donc de réfuter par exemple la théorie des cordes. En effet, il y a toujours des paramètres ajustables dans ces théories qui permettent de rendre suffisamment petite l'amplitude des ondes gravitationnelles avec ces modes "alternatifs" de polarisation. Si l'amplitude est trop faible, ces ondes échapperont à la détection.

Incidemment, à ma connaissance, il était déjà assez bien établi depuis un moment que les dimensions supplémentaires entraînaient génériquement l'apparition de modes B, simplement parce que les dimensions supplémentaires font en général apparaître des champs scalaires en quatre dimensions (on les appelle des champs modulaires) qui introduisent par essence des modes de polarisation B.

Aussi, du point de vue observationnel, il y a déjà de fortes contraintes sur l'existence de ces modes de polarisation alternatifs. La relativité générale ne permet pas à n'importe quel type de mouvement de distribution de matière de produire des ondes gravitationnelles. En termes techniques, il faut que ces distributions constituent ce qu'on appelle un moment quadripolaire. Les distributions ayant un moment dipolairemoment dipolaire ne rayonnent pas, contrairement à ce qui se passe avec des charges électriques dans le cadre de l'électromagnétismeélectromagnétisme.

Mais avec des alternatives à la théorie d'Einstein, un rayonnement dipolaire est parfois possible et il devrait produire des modes B si ceux-ci sont autorisés par la théorie. Les pulsars binaires sont en mesure de perdre de l'énergie sous forme d'ondes gravitationnelles de cette façon. Or les observations posent des contraintes drastiques sur ces émissions car elles ont tendance à faire perdre de l'énergie trop vite à ces systèmes, à tel point que le phénomène devrait se voir au niveau des mouvements de ces pulsars.

Il faudrait donc aussi que les auteurs expliquent pourquoi, dans le cadre qu'ils étudient, on pourrait avoir des émissions significatives d'ondes gravitationnelles avec des modes B avec des binaires de trous noirs; et pas avec des pulsars binaire. Sans une telle explication, il est fort probable que nous n'ayons que peu de chance d'observer ces modes de polarisation alternatifs, tant ils sont déjà contraints par les observations...».

La polarisation des ondes gravitationnelles et les dimensions supplémentaires des supercordes

Article de Laurent Sacco publié le 03/07/2017

La théorie des cordes fait usage de dimensions spatiales supplémentaires, introduites une première fois en physique par les théories de Kaluza-Klein. Bien que difficiles à observer, elles pourraient être mises en évidence grâce aux ondes gravitationnelles avec des détecteurs comme aLigo et Virgo.

La théorie des cordes requiert l'existence de dimensions spatiales supplémentaires pour obtenir une unification des champs de force et de matière, avec des équations décrivant des cordes qui vibrent, tout en respectant les lois de la mécanique quantiquemécanique quantique et surtout de la relativité restreinte. Quand les créateurs de cette théorie ont découvert ce fait au début des années 1970, ils étaient plutôt embarrassés car aucune expérience ne semblait montrer l'existence de ces dimensions spatiales dans lesquelles des objets auraient pu se déplacer en quittant notre espace-temps à quatre dimensions. Ils ont tenté de s'en débarrasser mais sans succès, et comme la théorie accomplissait des miracles, ils ne pouvaient se résoudre à l'abandonner.

Puis certains se sont souvenus des travaux de Théodor Kaluza et surtout de Félix Klein, avant la seconde guerre mondiale. Ils contenaient le début de la solution, il suffisait de refermer ces dimensions spatiales sur elles-mêmes pour les rendre plus petites qu'un atomeatome et ainsi empêcher que ceux-ci puissent s'échapper de notre monde. Toutefois, il était et il reste difficile de comprendre pourquoi ces dimensions ne sont pas entrées en expansion au moment du Big BangBig Bang et aussi pourquoi, aujourd'hui encore, elles semblent rester stables et de tailles constantes alors qu'elles auraient tout aussi bien pu s'effondrer comme le ferait une étoile en donnant un trou noir. Pour cette raison, le grand physicien et mathématicienmathématicien Roger PenroseRoger Penrose est plutôt sceptique envers la théorie des cordes. Son collègue Alain Connes est très critique lui aussi et il a depuis quelques décennies proposé une autre voie de recherche basée sur ses travaux en géométrie non commutative, lesquels lui ont valu la médaille Fields.

Malheureusement, tester l'existence de ces dimensions supplémentaires requiert a priori un accélérateur de particules aussi grand que la galaxiegalaxie. À la fin des années 1990, les physiciens ont pensé que ce n'était peut-être pas le cas si ces dimensions spatiales étaient plus grandes que ce que l'on imaginait au départ. Des arguments permettaient d'espérer voir des effets spectaculaires au LHC, et cela dès les premières collisions à basses énergies. L'effet le plus frappant aurait été la production de minitrous noirs s'évaporant par effet Hawking.

Des modes de Kaluza-Klein révélés par des collisions de trous noirs

Hélas, une fois de plus, la nature n'a pas été d'accord avec les attentes d'Homo sapiensHomo sapiens (quoiqu'elle le soit parfois, comme l'a montré la confirmation de l'existence du bosonboson de Brout-Englert-Higgs). Aujourd'hui, plus personne n'a de raisons de penser que ces dimensions supplémentaires seront visibles, même avec un super LHC de 100 km de circonférence.

Malgré tout, la nature est capable de faire des expériences pour nous avec des moyens colossaux, comme par exemple en faisant entrer en collision des trous noirs de plusieurs dizaines à plusieurs milliards de masses solaires. Deux physiciens de l'Institut Max-Planck de physique gravitationnelle, Lucena Gómez et David Andriot, ont été inspirés par cette possibilité. Ils viennent de déposer un papier à ce sujet sur arXiv.

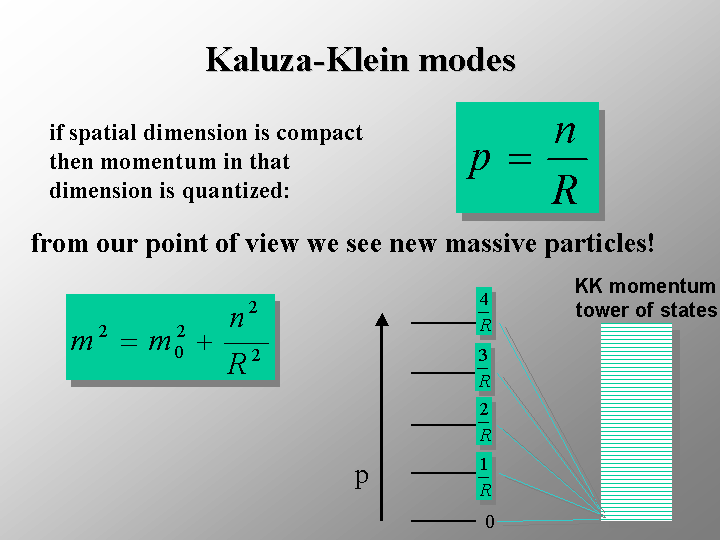
Si l'on considère l'espace-temps comme un instrument de musique qui peut vibrer, les dimensions spatiales supplémentaires sont donc un peu comme des touches additionnelles d'un piano dans une autre octave sur lesquelles il faudrait frapper particulièrement fort pour produire des notes, de hauteur plus élevée. En filant la métaphore, lors d'une violente collision de trous noirs, les ondes gravitationnelles émises vont contenir de plus hautes fréquences, lesquelles ne seraient pas produites si l'espace-temps n'avait que quatre dimensions. Techniquement, ces fréquences correspondent à ce que l'on appelle une tour de Kaluza-Klein pour les gravitons, les photonsphotons du champ de gravitation. On les appelle aussi des modes de Kaluza-Klein et ils correspondent à des gravitons de plus en plus massifs, à des modes de vibrationvibration des cordes de la théorie des cordes à plus hautes énergies.

Dans un modèle simple de dimension spatiale supplémentaire, une quatrième dimension est enroulée sur elle-même pour former un cercle de rayon R. Une particule quantique aura alors une composante d'impulsion P dans cette dimension qui est quantifiée à la manière d'une orbite d'électron dans un atome. Il apparaît alors une composante de masse supplémentaire dépendant d'un nombre entier N qui s'ajoute à celle de la particule dans sont état fondamental M₀. On obtient une tour de masses de Kaluza-Klein, un spectre de masse, qui devient continu lorsque R tend vers l'infini. © Joseph Lykken

Des ondes gravitationnelles polarisées détectables par aLigo et Virgo

Hélas, les fréquences de ces modes de Kaluza-Klein sont trop élevées pour qu'elles soient captées par des instruments comme aLigo et encore moins par eLisa. Heureusement, Gómez et Andriot ont montré que les dimensions spatiales supplémentaires avaient un autre effet, au niveau des modes de polarisation des ondes gravitationnelles, comme disent les physiciens.

Une façon de voir et de mesurer le passage d'une onde gravitationnelle en un point de l'espace est de regarder son effet sur la forme d'un ballonballon de football. L'un de ces effets est en gros de l'étirer-compresser en forme de ballon de rugby dont les axes vont osciller. Mais avec des dimensions spatiales supplémentaires, il existe un autre mode d'étirement qui fait gonfler le ballon avant de le ramener à sa taille normale (on parle de breathing mode, que l'on peut traduire en français par « mode de respiration »). Or, cet effet devrait être mesurable avec aLigo et son cousin européen Virgo, selon Gómez et Andriot.

Il serait ainsi possible de mettre en évidence ces dimensions spatiales supplémentaires. Voilà des raisons complémentaires de penser que la théorie des cordes est sur le bon chemin. En revanche, ne pas voir ce mode de polarisation pourrait être une réfutation de la théorie des cordes. Cependant, d'autres analyses théoriques sont sans doute nécessaires avant d'arriver à la conclusion que ce test est effectivement capable de falsifier, au sens fort, la théorie des cordes.

En revanche, observer ce mode ne serait sans doute pas encore une preuve suffisante de l'existence des dimensions spatiales supplémentaires car des modifications des équations de la théorie de la relativité générale ne supposant pas leur existence prédisent elles aussi ce mode. Il y a une dégénérescence, comme disent les physiciens. Affaire à suivre donc, au vu des réponses passionnantes que l'on pourrait obtenir au cours de la prochaine décennie.

Pour aller plus loin : une théorie purement géométrique des forces de la nature

Pour bien comprendre d'où vient l'intérêt d'ajouter des dimensions spatiales supplémentaires à l'espace-temps, il faut remonter aux premières tentatives de théorie unitaire des forces de la nature d'Einstein et Kaluza-Klein. Dans le cadre de la théorie de Kaluza-Klein, en étendant le nombre de dimensions spatiales de l'espace, on arrive à donner une interprétation géométrique de toutes les forces, et pas seulement de la gravitation, à partir de la géométrie-topologie de l'espace-temps.

Theodor Kaluza (à gauche) et Oskar Klein (à droite). Kaluza a proposé sa théorie en 1919. Elle n'unifiait que les forces connues de l'époque, à savoir, la gravitation et l'électromagnétisme. Klein est allé plus loin dans les années 1930 en complétant les idées de Kaluza et en utilisant les lois de la mécanique quantique. © Stanley Deser, université de Göttingen

Dans le cadre des équations d'Einstein reliant la courbure de l'espace-temps à une distribution d'énergie et d'impulsion, celles-ci s'écriront, quand la source du champ de gravitation est un champ électromagnétiquechamp électromagnétique, sous la forme suivante :

Le membre de gauche fait intervenir la géométrie de l'espace-temps. Il est construit à partir des dérivées spatiales et temporelles de la métrique de cet espace-temps.

Le membre de droite, lui, fait intervenir ce qu'on appelle « le tenseur impulsion-énergie des sources du champ de gravitation ». Ici, il s'agit d'un champ électromagnétique (em) pur. Dans le vide, les équations précédentes se réduiraient à l'équation donnée par l'annulation du tenseur de courbure contracté, dit « tenseur de Ricci » :

La magie de la théorie de Kaluza-Klein est qu'en écrivant cette dernière équation pour un espace-temps à cinq dimensions avec une dimension d'espace supplémentaire compactée sous forme de cercle, on retombe sur les équations du champ de gravitation en quatre dimensions couplées à un champ électromagnétique gouverné par les équations de Maxwelléquations de Maxwell ! On a donc les équations ci-dessous :

Le processus peut être généralisé, en ajoutant à notre espace-temps macroscopique à quatre dimensions des espaces géométriques microscopiques « internes » à n dimensions pour chaque point de cet espace. Ces dimensions supplémentaires doivent être compactifiées et de très petites tailles pour être compatibles avec le fait qu'on ne détecte pas ordinairement des dimensions spatiales de plus dans lesquelles les atomes pourraient se déplacer.

L'unification et les symétries géométriques

Les symétries géométriques des dimensions supplémentaires donnent alors les types de groupes de jauge associés aux forces et aux particules. Ce sont des groupes de Lie, dont l'importance en physique et en mathématiques ne saurait être sous-estimée. On voit là une nouvelle illustration de l'importance des symétries et de la théorie des groupes en physique.

Ainsi, selon une dimension supplémentaire donnant un cercle, la conservation de l'impulsion d'une particule le long de cette dimension compacte découle de l'invariance par rotation des équations selon ce cercle. Il se trouve que cette loi de conservation en cinq dimensions se traduit par la loi de conservation de la charge électrique en quatre dimensions associée au groupe de Lie U(1) des équations de Maxwell.

Une surface enroulée et compactifiée sous forme d'un cylindre ressemble de loin à un objet à une dimension, une ligne. Le groupe de rotation déplaçant un point d'un cercle en un autre est le groupe de Lie U(1). © physicsweb

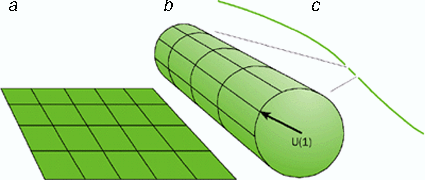
Si on avait une n-sphère, on en sortirait SU(2), SU(3), etc. Et donc, à chaque fois, la conservation des charges de QEDQED, QCD, et autres correspond juste à la conservation de l'impulsion en dimensions supplémentaires. Ces charges donnent aussi la valeur de la constante de couplage de ces interactions en liaison avec la géométrie et la taille des dimensions supplémentaires.