au sommaire
Deux scientifiques canadiens ont imaginé un scénario tordu pour donner plus de crédit à leur nouvelle méthode farfelue pour calculer le fameux nombre Π. Leurs outils principaux : une feuille d'aluminium et un fusil à pompe. Le tout publié dans arxiv, une revue où les scientifiques déposent volontiers leurs travaux
Le contexte : le fusil à pompe, l’alternative aux zombies
Imaginons un monde où un mal étrange frapperait le genre humain, transformant les victimes en morts-vivants dont la seule volonté serait de retirer l'humanité qui resterait à ceux qui sont encore épargnés... Heureusement, la nature amène à une telle diversité génétique que l'on peut espérer que parmi les sept milliards d'hommes et de femmes, certains seront en mesure de résister.
Néanmoins, la résistancerésistance doit s'organiser, et face à ces zombies décérébrés, la science demeure probablement l'un des piliers sur lesquels reposer. Mais avec quels moyens, si les accès aux supercalculateurs sont obstrués par une horde de revenants affamés ? Ceux du bord, évidemment.
Deux scientifiques canadiens, Vincent Dumoulin et Félix Thouin, de l'université de Montréal, offrent à tous les survivants la possibilité de poursuivre les calculs et de trouver une solution face à cette apocalypse zombie, en recourant à une arme probablement très utile dans ce cas de figure : le fusil à pompe. En voici le principe.
L’étude : du tir aux pi-geons à Monte Carlo
Prenons un carré de côté r=1, dans lequel on trace un quart de cercle qui commence dans un coin et finit dans celui opposé. La surface totale de ce carré est donc égale à 1. Celle du quart de cercle vaut Πr2/4 soit Π/4 puisque r2 = 1. Reste à déterminer la surface. Comment faire ?
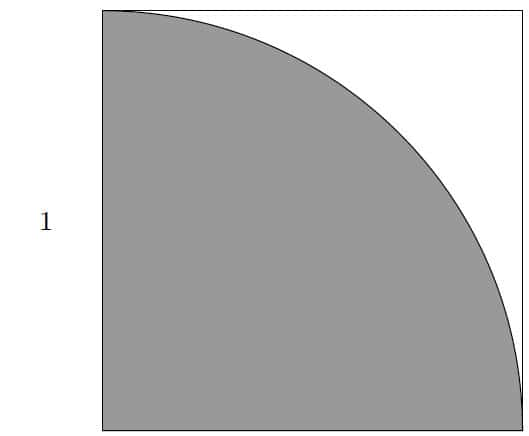
Représentation de l’arc de cercle dans un carré. La surface grisée équivaut à Π/4. © Dumoulin et Thouin, arXiv
Voici une idée simple : il suffit de disposer de très nombreux grains de taille identique et de les disposer aléatoirement de manière à recouvrir une grande partie du dessin. En les comptant un à un, on peut obtenir un ratio entre la surface totale du carré et celle de l'arc de disque et, à terme, estimer Π. On peut le faire avec des grains de riz par exemple, mais en cas d'apocalypse plus que dans toute autre situation, il ne faut pas jouer avec la nourriture. C'est là que le fusil à pompe intervient.
Cette approximation statistique est une méthode dite de Monte Carlo (qui utilise un moyen aléatoire). Les deux chercheurs ont choisi un Mossberg 500, l'une des armes à feu les plus courantes aux États-Unis voisins, avec lequel ils ont tiré à 200 reprises sur une cible en aluminium, à 20 m de distance. Les cartouches explosent en de multiples éclats, si bien qu'en tout, les auteurs ont compté 30.857 trous de plomb sur la cible.

Un exemple de fusil à pompe Mossberg 500. Cette arme est prisée aux États-Unis, notamment pour son bon rapport qualité/prix. Même la police en est équipée. © Fluzwup, Wikipédia, cc by sa 3.0
Ensuite, malheureusement, il ne suffit pas de compter. Il y a une petite subtilité essentielle. En fonction du ventvent, de la hauteur du fusil au moment du tir et d'autres paramètres incontrôlables, la répartition de chacun de ces points n'est pas aléatoire. Il leur a donc fallu estimer la densité de déflagrations selon la zone de la cible. Ainsi, 10.000 des impacts ont permis une telle cartographie. Avec les 20.857 points restants, les auteurs ont pu faire leurs comptes et trouver une valeur de Π égale à 3,131. Soit une approximation précise à 99,66 %.
L’œil extérieur : Pi n’a rien d’absurde
Évidemment, cette étude, bien que basée sur des calculs sérieux, est tout à fait loufoque. Néanmoins, elle montre qu'avec de petits moyens, il est possible de retrouver des constantes mathématiques essentielles, puisque Π fait l'objet d'études depuis l'Antiquité.
Il existe d'autres méthodes, plus simples, pour aboutir à des approximations de ce nombre infini, à l'aide d'une roue par exemple. Mais celle-ci devait être trop classique aux yeuxyeux des deux chercheurs, désireux de créer leur propre méthode... par l'absurde.






![Ensemble de Julia (C = [0.285, 0.01]), une Fractale. Image réalisée à partir d'un programme rédigé par l'auteur, et nommé « Julia dream », d'après une mélodie de Pink Floyd. © Solkoll - Domaine public
Ensemble de Julia (C = [0.285, 0.01]), une Fractale. Image réalisée à partir d'un programme rédigé par l'auteur, et nommé « Julia dream », d'après une mélodie de Pink Floyd. © Solkoll - Domaine public](https://cdn.futura-sciences.com/cdn-cgi/image/width=200,quality=60,format=auto/sources/images/dossier/90/02-90.jpg)
















