au sommaire

Srinavasa Ramanujan (1887 - 1920)
Le style Ramanujan
Pour situer le contexte, il faut rappeler que Ramanujan, autodidacte, était doué d'une intuition prodigieuse déconcertante. Même pour des mathématiciensmathématiciens de premier plan (tels que Hardy ou Littlewood avec qui il a beaucoup collaboré lors de son séjour à Cambridge), il était très difficile de suivre toutes les étapes de son raisonnement. Par ailleurs, Ramanujan compilait ses travaux dans des carnets presque sans explication : au terme d'un travail de titantitan dirigé par B. Berndt, les carnets n'ont été complètement publiées que récemment (cinq volumes de 1985 à 1997).
Au printemps 1976, le professeur G. Andrews découvre au Trinity College de Cambridge une collection de 138 pages de la main de Ramanujan : c'est le fameux « carnet perdu », écrit peu de temps avant sa mort prématurée. Le carnet perdu contient certainement les travaux les plus profonds de Ramanujan, et notamment des indices sur les mock theta functions : c'est un peu comme si G. Andrews avait découvert la dixième symphonie de Beethoven ! Les mock theta functions étaient déjà connues par une lettre écrite à Hardy en janvier 1920 (la dernière et la seule au retour de Ramanujan en Inde), mais dont une partie a hélàs été perdue. Pour étudier ces objets, il ne reste donc que bien peu d'éléments, ce qui fait dire à K. Ono : « Imaginez que l'on vous présente une liste d'un millier de mots au hasard en vous disant qu'ils forment le plus beau poème jamais écrit... C'est en quelque sorte ce que Ramanujan nous a lègué. » ("Imagine stringing together a thousand random words and then saying you've come up with the most beautiful poetry. That's essentially what Ramanujan did to us.")
Avant d'évoquer les travaux de K. Bringmann et K. Ono, nous vous proposons dans un premier temps de goûter à la beauté de ces mathématiques, dans un langage aussi élémentaire que possible compte tenu de leur complexité. Aussi, que le lecteur nous pardonne de faire usage de notations mathématiques pour lesquelles il est néanmoins invité à demander toutes les précisions dont il aurait besoin sur le forum (suivre le lien "Commenter cette news ou lire les commentaires" en bas de page).
Des fonctions elliptiques aux fonctions modulaires
D'apparence simple, le calcul de la longueur d'un arc d'ellipse constitue en réalité un vrai casse-tête ! L'intégrale donnant la solution est pour le moins particulièrement délicate à déterminer... (pour tout dire, ce n'est pas possible à l'aide des fonctions usuelles).
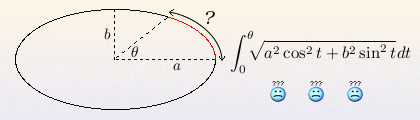
Le calcul de la longueur d'un arc d'ellipse fait intervenir une « intégrale elliptique » peu évidente...
Crédits : S. Tummarello
Au XIXème siècle, l'étude de ce type d'intégrale débouchera finalement, avec la maîtrise des nombres complexes, sur la théorie dite des fonctions elliptiques. Ces nouvelles fonctions, définies sur le plan complexe, ont été intensément étudiées et leur caractéristique majeure est de respecter deux symétries par translation (on dit qu'elles sont doublement périodiques). En effet, si le sinus admet pour période , de sorte que
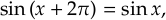
les fonctions elliptiques admettent deux périodes et
, qui sont des nombres complexes, telles que
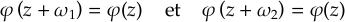
Du point de vue géométrique, celà revient à dire que l'on peut paver le plan complexe avec des parallélogrammes, et que la connaissance de la fonction sur l'un de ses parallèlogrammes (dit fondamental) détermine la fonction sur le plan en entier. Mieux encore, pour ceux qui se souviennent des collages en topologie (cf. notre article sur G. Perelman), le domaine naturel de définition d'une fonction elliptique est en réalité un tore.
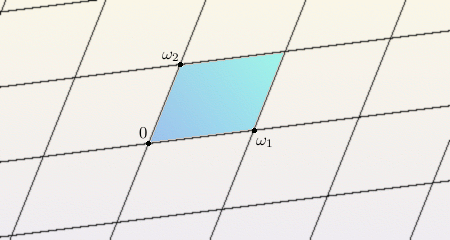
Les fonctions elliptiques sont définies sur un pavage du plan réalisé à l'aide de parallélogrammes.
En bleu : un « parallélogramme fondamental ».
Crédits : S. Tummarello
Avec le développement de cette théorie apparaissent spontanément des « invariants », de nouvelles fonctions vérifiant des propriétés originales, comme le « discriminant modulaire » , un objet essentiel dans cette branche des mathématiques. Ces fonctions respectent un autre type de symétrie, un peu plus exotiqueexotique comme nous allons le voir. Les mathématiciens remarquent par exemple que pour des entiers a, b, c, d choisis tels que ad-bc=1, le discriminant modulaire se transforme (par homographie) selon la règle :
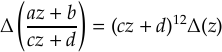
D'une manière générale, les fonctions dites modulaires (car liées au « module » des fonctions elliptiques) vérifient une symétrie de la forme :
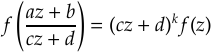
où l'entier k est baptisé « poids ».
Toutes ces formules peuvent paraître au premier abord bien peu sympathiques. Mais il faut les appréhender dans un cadre convenable, et à ce dessein tirer parti de l'une des plus grandes prouesses du XIXème siècle : les géométries non-euclidiennes. Car, tout comme les symétries des fonctions elliptiques se résument à deux translation du plan (euclidien), celles des fonctions modulaires sont des symétries du plan hyperbolique (appelé aussi demi-plan de Poincaré). La figure ci-dessous donne un exemple de domaine fondamental (l'analogue du parallélogramme fondamental), dont la connaissance permet de reconstituer le plan hyperbolique en son entier (par un pavage qui ressemble à une sorte de puzzle géométrique).

Les fonctions modulaires sont définies de manière naturelle sur le demi-plan de Poincaré, dont la géométrie est non-euclidienne (hyperbolique). Ce plan est pavé par des « triangles ».
Crédits : S. Tummarello
Ramanujan, dont le génie à conduit à redécouvrir presque seul la théorie des fonctions elliptiques et modulaires, a fait la remarquable démonstration de la puissance et de la richesse de ces idées. L'exemple de la fonction (lire « tau ») en est assez emblématique.
La fonction « tau » de Ramanujan
Reprenons l'exemple du discriminant modulaire , dont la définition s'écrit
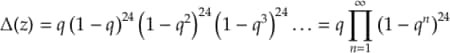
où
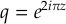
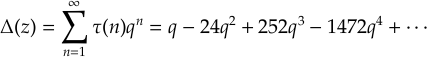
c'est-à-dire aux nombres , qui ont le bon goût de tous être entiers.
L'une des premières conjectures de Ramanujan à ce sujet a été de dire que si m et n sont deux nombres premiers entre euxnombres premiers entre eux, alors
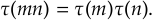
et que si p est un nombre premier et s un entier positif, alors
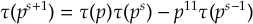
Ces deux formules ont été démontrées par Mordell en 1917, mais elles découlent de manière bien plus naturelle de la théorie de Hecke (1930), qui donnera naissance à toute la théorie moderne des formes automorphesautomorphes, un sujet de première instance en arithmétique.
Ramanujan a par ailleurs deviné que si p est un nombre premier, alors on devrait avoir
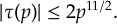
Cette question compte parmi les plus difficiles qu'il ait posées : elle ne fut résolue qu'en 1974 par Deligne, comme conséquence de théorèmesthéorèmes très techniques (les conjectures de Weil). Citons enfin la congruence relativement plus simple à démontrer :
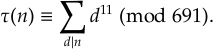
Il se trouve que Serre et Swinnerton-Dyer ont resitué ce résultat dans la « théorie des représentations l-adique du groupe de Galois absolu », c'est-à-dire en termes plus concrets dans le langage qu'Andrew Wiles a utilisé pour démontrer le célèbre dernier théorème de Fermat !
Il serait bien entendu malhonnête de prétendre que Ramanujan avait des vues précises sur des théories modernes aussi complexes que celle de Serre-Deligne. Néanmoins, il en est à bien des égards le précurseur, comme illustré ici au sujet de la fonction , mais aussi comme son oeuvre entière en témoigne.
Partitions d'un entier et conjecture d'Andrews-Dragonette
Malgré leur simplicité apparente, les partitionspartitions sont au coeur des travaux modernes et nous en avions déjà parlé au sujet d'A. Okounkov, l'un des quatre lauréats de la médaille Fields 2006. Pour rappel, une partition d'un nombre entier est une suite décroissante de nombres positifs dont la somme vaut
. Il y a par exemple cinq partitions possibles pour le nombre 4 :
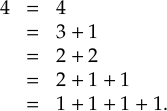
Depuis Euler, on sait que le nombre p(n) de partitions d'un entier n (nous venons par exemple de voir que p(4)=5) est codé dans la série génératrice
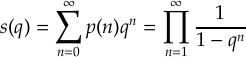
dont on voit qu'elle ressemble fort au discriminant modulaire (le lecteur initié se convaincra sans peine que
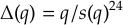
A l'aide de la « méthode du cercle » qu'ils ont imaginée, Ramanujan et Hardy ont pu démontré en 1918 que lorsque n croît vers l'infini,
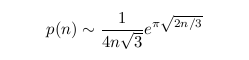
et Rademacher a fourni en 1937 une formule exacte (en usant du fait que s(q) est une forme modulaire de poids 1/2).
Les travaux de K. Bringmann et K. Ono portent sur un problème similaire : quel est le nombre de partitions de rang pair ou impair pour un entier donné ? Dyson avait en effet introduit en 1944 la notion de rang d'une partition afin de tenter d'expliquer certaines congruences (dues elles aussi à Ramanujan) comme
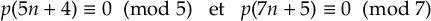
Pour calculer le rang d'une partition, il suffit de retrancher au plus grand terme le nombre total de termes : par exemple, le rang de la partition 22=19+3 vaut 19-2=17 tandis que celui de 22=5+5+4+4+2+1+1 vaut 5-7=-2. De même que pour p(n), il est naturel d'étudier une série génératrice : en notant respectivement et
le nombre de partitions paires et impaires d'un entier
, et en formant la différence
, la série
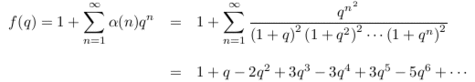
n'est autre que l'une des 22 mock theta functions figurant dans la lettre de Ramanujan à Hardy de 1920 ! Cette dernière comprend en outre l'estimation
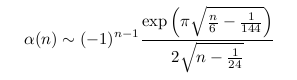
que Dragonette a prouvée dans sa thèse en 1951, sous la direction de Rademacher. Avec ce dernier, Andrews améliora en 1964 l'estimation au point de presque obtenir une formule exacte : c'est la conjecture d'Andrews-Dragonette. Suite aux percées de K. Bringmann et K. Ono, la conjecture est désormais un théorème décrivant des formules fermées pour et
(trop longues à exposer pour les évoquer ici).
Les mock theta functions et les formes de Maass
Mais le mérite des deux mathématiciens est surtout d'apporter un éclairage nouveau et fécond sur ces mock theta functions, dont même la définition est peu claire, compte tenu du peu que nous a laissé Ramanujan. En effet, après Sander Zwegers qui en 2002 a magistralement montré comment elles s'interprètent en tant que « formes modulaires vectorielles » (et de plus en tant que fonctions propres d'un certain opérateur différentiel), K. Bringmann et K. Ono ont relié le sujet à un des prototypes de formes automorphes, appelées formes de MaassMaass. Ces fonctions, imaginées par Maass en 1949, généralisent la notion de forme modulaire : sans entrer dans trop de détails, retenons que les formes de Maass (faibles) admettent un développement de Fourier de la forme
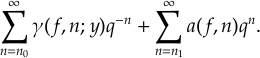
Ainsi, tandis que les coefficients
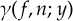
Leurs recherches les ont enfin conduit à proposer un schéma général prometteur, où par exemple le nombre de partitions se traduit comme une « trace » liée à un relèvement d'une certaine forme modulaire dans un espace de Calabi-Yau. Ce cadre pourrait bien être celui permettant de comprendre les dernières formules de Ramanujan, dont le génie n'a cessé d'inspirer les mathématiciens depuis des décennies.






















