Les mathématiciens sont des artistes : l'IRM le confirme

L'idée qu'il puisse exister un lien profond entre l'activité d'un mathématicienmathématicien et celle d'un artiste est généralement déconcertante pour les non-mathématiciens. Nombreux sont ceux qui ne retiennent des mathématiques que l'idée d'une pratique technique et aride, où le raisonnement logique domine. Cela semble n'avoir rien en commun avec l'émotion, la créativité et la beauté, toutes choses que le poète, le musicien, le peintre ou d'autres artistes mettent en avant quand ils parlent de leurs travaux.

Pourtant, les mathématiciens (et il n'est nul besoin d'entendre par là uniquement les mathématiciens professionnels) ont une tout autre vision des choses. Quelques-uns vont peut-être dire qu'ils aiment résoudre des énigmes et des puzzles, mais tous témoignent d'expériences émotionnelles intenses parfaitement comparables à celles qu'éprouve un artiste. À en entendre certains, le besoin de faire des mathématiques, la fascination esthétique qu'elles engendrent, qu'elles soient pures ou appliquées aux sciences comme la physique théorique, sont aussi impérieux et irrésistibles que ceux à l'origine des œuvres d'artistes comme Hölderlin, Léonard de VinciLéonard de Vinci ou Bach. Les théories et les équations mathématiques, même celles que l'on retrouve en physique théorique (des équations de la relativité générale à celles de la théorie quantique des champs en passant par les équations de Maxwell et de Navier-Stokes), sont perçues comme des œuvres d'art à part entière.

Il semble que ces idées soient très anciennes, surtout chez les mathématiciens-philosophes grecs. Chez Pythagore comme chez Platon, la géométrie, l'arithmétique, la musique et l'astronomie sont liées au sein de la philosophie. Elles participent des idées de beauté, d'harmonie, de mesure et de raison et sont considérées comme ayant un intérêt intrinsèque, en elles-mêmes, par delà toute application pratique possible, même si elles donnent les clés d'une connaissance du monde.

Les mathématiques et l'harmonie du monde

On sait par exemple que dans le Timée, Platon expose une sorte de théorie des particules élémentairesparticules élémentaires du cosmoscosmos en utilisant des considérations sur les polyèdres réguliers. Il y a cette perception que le monde doit être construit non à base d'objets matériels mais de formes mathématiques pures et élégantes. Heisenberg racontera plus tard comment la lecture du Timée l'avait mené sur la voie de la découverte des équations de la mécanique quantiquemécanique quantique sous leur forme matricielle. Plus tard, les conceptions de Platon le pousseront à mettre en avant l'idée que les particules élémentaires sont avant tout des symétries dans les équations de la théorie quantique des champs. Le modèle standardmodèle standard en physique des particules a donné une confirmation spectaculaire de ces idées. À travers la théorie des groupes, les symétries y acquièrent une importance et une puissance extrêmes.

Répétons-le, pour des mathématiciens comme l'étaient Platon et Pythagore, les mathématiques ne doivent pas être cultivées uniquement en vue d'applications pratiques, mais pour ce qu'elles sont en elles-mêmes, comme la musique, la peinture ou la sculpture. L'une des apologies les plus connues de ce point de vue se trouve dans les déclarations du mathématicien allemand Gustav Jacobi au XIX^e siècle : « Monsieur Fourier avait l'opinion que le but principal des mathématiques était l'utilité publique et l'explication des phénomènes naturels. Un philosophe tel que lui aurait dû savoir que le but unique de la science, c'est l'honneur de l'esprit humain et que, sous ce titre, une question de nombres vaut bien une question de système du monde ». Le mathématicien Jean Dieudonné, l'un des fondateurs du célèbre groupe Bourbaki, ne s'y est pas trompé. Cette citation se trouve en exergue d'un très beau livre qu'il a écrit pour l'amateur passionné, lui permettant de visiter la cathédrale des mathématiques dans l'état de constructionconstruction qu'elle a atteint au XX^e siècle.

L'importance de la beauté en mathématique que l'on trouve chez les Grecs, on la retrouve aussi chez les mathématiciens du XX^e siècle. Pour preuve, voici quelques-unes des déclarations parmi les plus célèbres.

Les mathématiques, la musique de la raison

La première nous vient du mathématicien britannique G. H. Hardy (1877-1947), grand spécialiste de l'extraordinaire théorie analytique des nombres et bien connu pour ses travaux avec le « mathémagicien » indien Srinivasa Ramanujan. « Les schémas du mathématicien, comme ceux du peintre ou du poète, doivent être beaux ; les idées, comme les couleurscouleurs ou les mots, doivent s'assembler de façon harmonieuse. La beauté est le premier test : il n'y a pas de place durable dans le monde pour les mathématiques laides. »

La deuxième est de David Hilbert, probablement avec Henri Poincaré le mathématicien le plus important et le plus universel entre 1900 et 1920. Ses travaux couvrent en effet de vastes domaines allant de la théorie algébrique des nombres à l'analyse fonctionnelle (avec les fameux espaces portant son nom), en passant par la théorie des invariantsinvariants et celle des fondements des mathématiques (avec Paul Bernays). Pour Hilbert, « dans un certain sens, l'analyse mathématique est une symphonie de l'infini ».

La troisième émane d'Hermann Weyl, l'élève le plus doué d'Hilbert selon Dieudonné, à qui l'on doit d'importants travaux sur la topologie des surfaces de Riemannsurfaces de Riemann et surtout la théorie des groupes de Lie, à la frontière entre la géométrie, l'algèbre et la physique théorique. « Dans mon travail, j'ai toujours tenté d'unir le vrai et le beau, et lorsque je devais faire un choix entre les deux, je choisissais d'ordinaire le beau. »

L'identité d'Euler à l'IRM

Pour ceux qui ne seraient pas encore convaincus que les mathématiciens et les amateurs éclairés de mathématiques ont une âme d'artiste, le neurobiologiste Semir Zeki vient fournir du grain à moudre.

Le chercheur est parti d'un constat simple que nous avons déjà évoqué. « Pour beaucoup d'entre nous, des formules mathématiques semblent sèches et inaccessibles, mais pour un mathématicien, une équation peut incarner la quintessence de la beauté. La beauté d'une formule peut résulter de la simplicité, de la symétrie, l'élégance ou l'expression d'une vérité immuable. Pour Platon, le caractère abstrait des mathématiques exprimait le sommet ultime de la beauté. » Mais pour un spécialiste du cerveaucerveau comme lui, « on est alors curieux de savoir si l'expérience de la beauté provenant d'une source aussi hautement intellectuelle et abstraite que les mathématiques est en corrélation avec l'activité dans la même partie du cerveau émotionnel que celle dérivée de sources plus fondées sur la perception des sens ».

Cherchant à en avoir le cœur net, comme lui et ses collègues l'expliquent dans un article en accès libre publié dans Frontiers in Human Neuroscience, il a décidé d'utiliser les l'IRMIRM pour étudier l'activité du cerveau de 15 mathématiciens. Le protocoleprotocole de l'expérience réalisée n'est pas difficile à comprendre. On a commencé par soumettre aux cobayes 60 formules ou équations mathématiques en leur demandant de les noter chacune sur une échelle allant de -5 (affreuse) à 5 (sublime). Deux semaines plus tard, l'expérience a été répétée, mais cette fois-ci en observant à l'IRM ce qui se passait dans le cerveau des mathématiciens. Les neurobiologistes ont alors constaté que l'activité du cortex orbitofrontal médian se corrélait bien avec l'intensité de l'expérience de la beauté associée aux formules mathématiques jugées comme telles par les mathématiciens. Or, on sait qu'il en est de même pour le sentiment de beauté associé à des œuvres d'art, notamment avec la musique.

L'identité d'Euler semble trop belle pour être vraie : elle l'est pourtant bel et bien. Elle rassemble en une seule équation les nombres les plus magiques des mathématiques : 1, 0 et les nombres transcendants que sont π et e, ainsi que le nombre imaginaire i. © DP

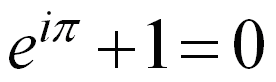
Le cerveau et la beauté des mathématiques

Sans surprise, sont arrivées en tête du classement la fameuse identité d'Euler liant les nombres les plus importants des mathématiques ainsi que les conditions de Cauchy-Riemann évoquant la puissante et élégante théorie des fonctions analytiques. En dernier, on trouve l'une des séries infinies de Ramanujan permettant de calculer le nombre π ainsi que, et c'est plus surprenant (au moins pour l'auteur de cet article), la fameuse relation fonctionnelle de Riemann associant la fonction zêta de Riemann et la fonction gamma d'Euler.

Pour Zeki, l'affaire est entendue : « Nous avons trouvé que, comme avec l'expérience de la beauté visuelle ou musicale, l'activité dans le cerveau est fortement liée à l'intensité de l'expérience de la beauté déclarée, même dans cet exemple où la source de la beauté est très abstraite. Cela répond à une importante question dans le domaine de l'esthétique, une de celles débattues depuis l'Antiquité, à savoir si les expériences esthétiques peuvent être quantifiées. »