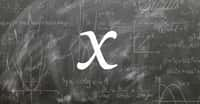au sommaire

Grigori Perelman
Qu'est-ce que la topologie ?
La topologie est une branche jeune des mathématiques et sa naissance remonte à environ trois siècles avec Leibniz et surtout Euler1. Un problème bien connu de l'époque est celui des ponts de Königsberg : peut-on organiser dans cette ville une promenade dont le trajet serait une boucle qui passe une fois et une seule par chacun des sept ponts ? Cette question, qui relève de la géométrie, ne fait pourtant appel à aucune notion de distance ou d'échelle, car seule compte la disposition relative des ponts. Les hypothèses peuvent par conséquent être codées par un graphe où l'on cherche un cycle eulérien, à savoir une boucle passant exactement une fois par chacune des arêtes.
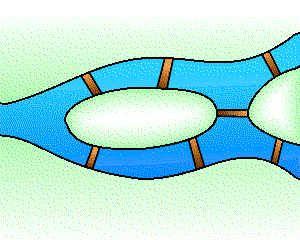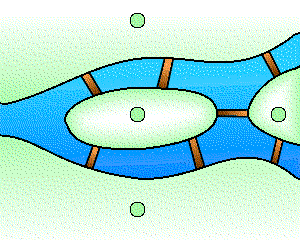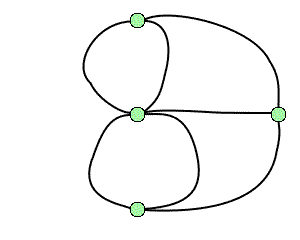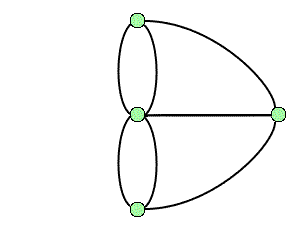
Le problème des ponts de Königsberg et le graphe associé.
Crédits : S. Tummarello
La topologie est ainsi la branche des mathématiques où, à l'instar de cette devinette, la géométrie est souple : deux configurations deviennent équivalentes dès qu'elles ont « la même forme ». Il n'y a par exemple aucune différence de nature topologique entre une tâche d'encre et un disque, entre un carré et un cercle, ou encore entre une sphère et un ellipsoïde. Cette propriété d'avoir la même forme s'exprime rigoureusement en mathématiques par la notion d'homéomorphisme.

Une tâche d'encre et un disque sont homéomorphes...
Crédits : S. Tummarello

... tout comme un cercle et un rectangle,
Crédits : S. Tummarello

... ou encore une sphère et un ellipsoïde.
Crédits : S. Tummarello
En 1736, Euler résoud le problème des ponts de Königsberg en introduisant le « degré » d'un sommet dans un graphe (c'est le nombre d'arêtes incidentes à ce sommet). Comme la présence d'au moins un sommet de degré impair interdit l'existence d'un cycle eulérien, et qu'il y en a quatre pour le graphe des ponts de Königsberg, l'énigme n'a donc pas de solution. De manière plus générale, l'objet de la topologie est précisément de mettre en évidence des invariants qui rendent compte de certaines propriétés des objets qu'elle étudie. Parmi les premiers invariants mis à jour, citons aussi la célèbre caractéristique d'Euler-Poincaré, découverte par Euler en 1752 : dans un polyèdre convexeconvexe2, le nombre de ses faces et sommets, diminué du nombre de ses arêtes, vaut toujours 2.
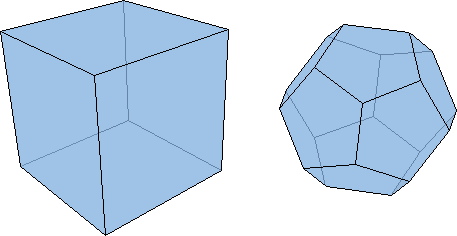
Un cube possède 6 faces, 12 arêtes et 8 sommets : sa caractéristique d'Euler-Poincaré vaut donc 6+8-12=2.
Celle d'un dodécaèdre vaut également 2 : 12 faces, 30 arêtes et 20 sommets (12+20-30=2).
Crédits : S. Tummarello
Plus récemment et dans un autre registre, la théorie des nœuds, étudiant les différentes configurations que peut prendre une boucle dans l'espace, connaît une seconde jeunesse depuis la découverte en 1983 de nouveaux invariants (les polynômes de Jones). Toutefois, certains nœuds admettant des polynômes de Jones identiques, la recherche d'invariants à même de distinguer tous les nœuds demeure largement ouverte, preuve que la topologie recèle encore aujourd'hui de nombreux mystères.
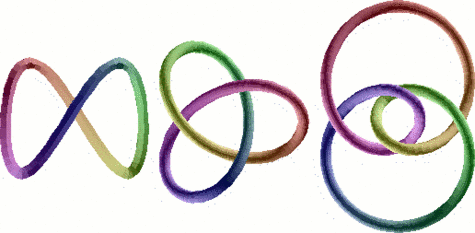
De gauche à droite, le nœud trivial (un cercle tordu), le nœud de trèfle et le nœud en huit : ces trois nœuds sont tous distincts, au sens où il faudrait les couper pour passer continûment de l'un à l'autre.
Crédits : S. Tummarello
Avec du papier et un peu de colle...
Les objets de la topologie, nommés variétés topologiques, forment un zoo difficilement concevable tant il est riche : la tâche titanesque d'y mettre un peu d'ordre incombe naturellement aux mathématiciensmathématiciens, et nous verrons qu'ils n'ont pas manqué d'imagination pour relever le défi. Mais avant de venir aux idées novatrices de Poincaré en particulier, partons à la rencontre de quelques célébrités omniprésentes dans les ouvrages de topologie...
Nous avons déjà rencontré des graphes et des nœuds, qui sont de dimension 1, et les figures les plus simples après les courbes sont bien entendu les surfaces (les variétés de dimension 2). Puisqu'un disque est homéomorphe à un rectangle (plein), il suffira d'une bande de papier et d'un peu de colle pour construire notre première variété : le cylindre, qu'un enfant saurait aisément fabriquer en faisant coïncider deux côtés opposés. L'opération mathématique correspondante n'est d'ailleurs guère plus complexe dès que l'on dispose de « colle topologique » (la notion d'ensemble quotient). Ce collage est symbolisé par le schéma à gauche de l'illustration : les côtés flèchés doivent se confondre après "pliage".
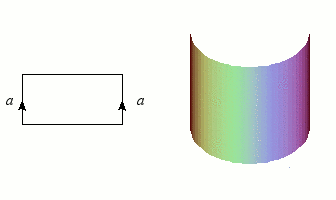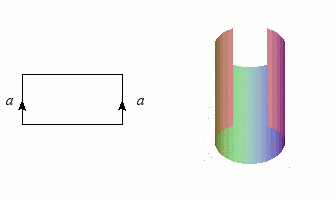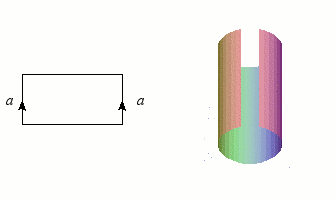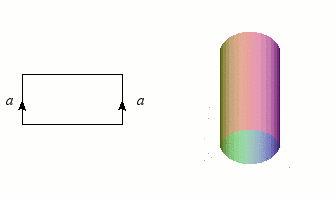
Construction du cylindre par collage des côtés d'un rectangle.
Crédits : S. Tummarello
Pourvu que la bande de papier soit assez longue, il est également possible de la courber d'un demi-tour avant le collage : on obtient alors le célèbre ruban de Möbius, en mémoire du mathématicien qui l'a imaginé en 1858. C'est l'exemple le plus simple de variété non-orientable : le ruban de Möbius n'admet en effet qu'une seule face, il n'y a ni recto ni verso. Sur le schéma, les flèches sont opposées pour indiquer l'inversion des orientations des côtés à coller.

Construction du ruban de Möbius.
Crédits : S. Tummarello
Revenons maintenant au cylindre, dont nous allons superposer les bords (les deux cercles) : le résultat forme une bouée, ou plus exactement un tore. Tout comme la sphère, le tore est une variété sans bord et orientable, mais il s'en distingue nettement par ce « trou » qui permet heureusement au baigneur imprudent de passer les bras.
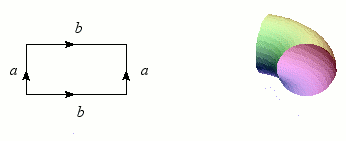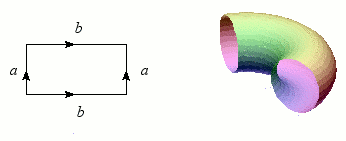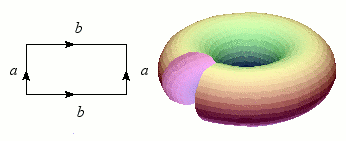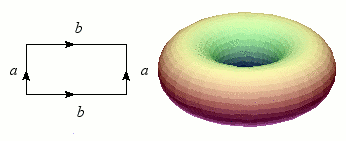
Construction du tore.
Crédits : S. Tummarello
Nous avons vu qu'il est relativement simple de former un ruban de Möbius en incurvant une bande de papier. En revanche, coller les bords d'un cylindre avec des orientations opposées contitue un véritable challenge ! L'opération nécessite en effet de passer par l'intérieur du cylindre, d'où un croisement problématique dans notre espace à trois dimensions. Mais à cœur vaillant rien d'impossible : l'objet singulier obtenu s'appelle une bouteille de Klein, du nom du géomètregéomètre allemand qui l'a inventé à la fin du XIXème siècle.

Une bouteille de Klein en verre réalisée par Clifford Stoll.
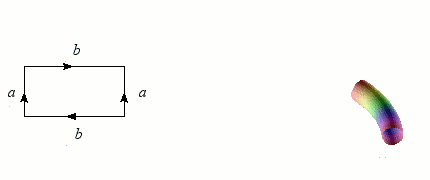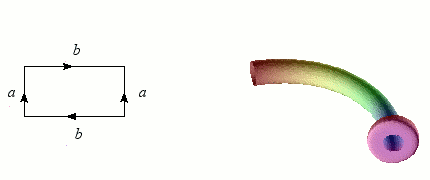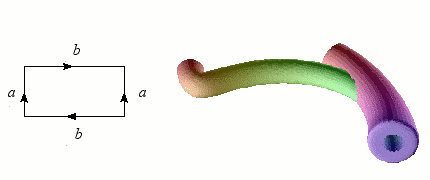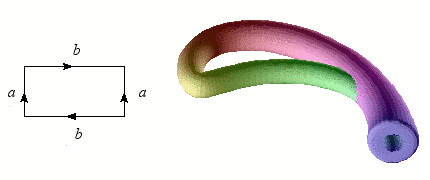
Construction de la bouteille de Klein.
Crédits : S. Tummarello
Toutefois, puisque l'on part d'un rectangle dont uniquement les bords sont recollés sur eux-mêmes, il ne doit pas y avoir d'intersection comme celle visible sur les représentations ci-dessus. La difficulté naît de ce que nous vivons dans un espace à trois dimensions d'espace, et que pour visualiser correctement la bouteille de Klein, il faudrait une dimension supplémentaire : l'intersection de la bouteille de Klein avec elle-même est ainsi tout aussi fictive que celle que nous sommes habitués à ignorer dans la représentation en perspective d'un cube.
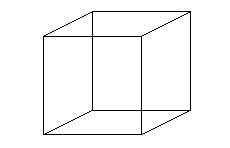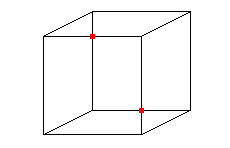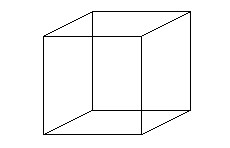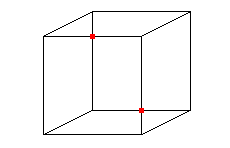
Ceci est-il un cube ou 12 segments du plan ? Si nous sommes capables d'imaginer le volume, les points d'intersections marqués en rouge existent bel et bien dans le plan.
Crédits : S. Tummarello
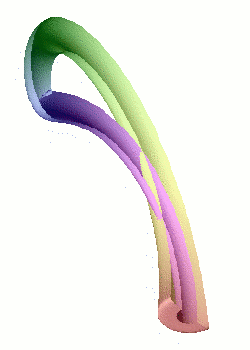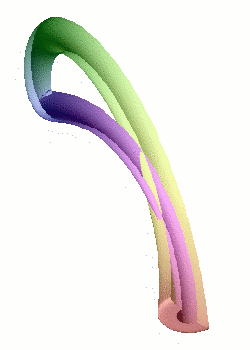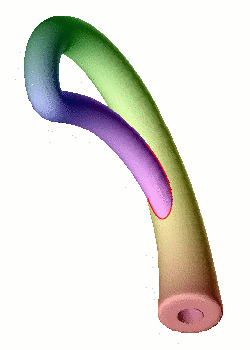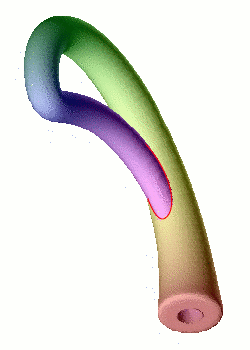
La modélisation d'une bouteille de Klein dans notre espace à trois dimensions implique inévitablement une auto-intersection (en rouge) : il s'agit du même phénomène de projection que pour la représentation plane du cube.
Crédits : S. Tummarello
Passé le fait que la bouteille de Klein "vit" dans un espace à quatre dimensions, elle constitue surtout le premier exemple de variété à la fois sans bord et non-orientable : contrairement à la sphère ou au tore, elle n'a ni intérieur, ni extérieur !
Au demeurant, rien n'empêche d'imaginer d'autres collages et de remplacer les côtés d'un rectangle par ceux d'un polygone : on obtient alors une multitude de variétés aux propriétés diverses : avec ou sans bord, orientables ou non, avec un ou plusieurs "trous", etc. Muni d'un peu de colle et d'imagination, les possibilités sont déjà pléthoriques !
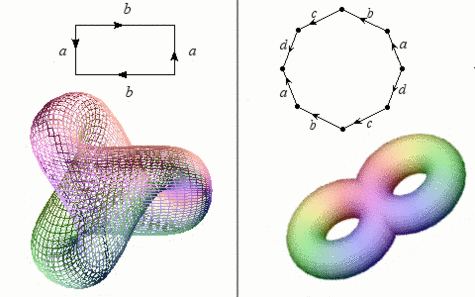
À gauche, le « plan projectif réel » est, à l'instar de la bouteille de Klein, une variété délicate à représenter en trois dimensions (les intersections sont encore une fois fictives).
Un collage particulier des côtés d'un octogone donne un « tore à deux trous », à droite.
Crédits : S. Tummarello
Toutes ces constructionsconstructions n'en seraient restées qu'au stade des curiosités si les applicationsapplications de la topologie n'avaient pas été si nombreuses, y compris hors du champ d'investigation des mathématiques : en tant qu'outil, en physiquephysique théorique par exemple, mais aussi en tant que source d'inspiration comme l'illustrent la « morphogenèsemorphogenèse » de R. Thom ou plus récemment « l'universunivers chiffonné » de J.P. Luminet (dont le principe repose essentiellement sur des recollements de même nature que ceux décrits précédemment, appliqués cependant à des variétés de dimension 3).
Poincaré, fondateur de la topologie algébrique
Le rôle crucial qu'était amené à jouer la topologie en mathématiques a tôt été reconnu par Poincaré, qui écrit3 : « Toutes les voies diverses où je m'étais engagé successivement me conduisaient à l'Analysis Situs4. J'avais besoin des données de cette Science pour poursuivre mes études sur les courbes définies par des équationséquations différentielles et pour les étendre aux équations différentielles d'ordre supérieur, et, en particulier, à celles du problème des trois corps. J'en avais besoin pour l'étude des fonctions non uniformes de deux variables. J'en avais besoin pour l'étude des intégrales multiples et pour l'application de cette étude au développement de la fonction pertubatrice. Enfin j'entrevoyais dans l'Analysis Situs un moyen d'aborder un problème important de théorie des groupes, la recherche des groupes discrets ou des groupes finis contenus dans un groupe continu donné. »
Pourquoi ne peut-on pas déformer, sans la déchirer, une sphère en un tore ? Comment décrire, et surtout caractériser, les différentes variétés ? Si nous avons entrevu quelques propriétés relativement élémentaires des variétés (existence d'un bord, orientabilité), bien d'autres avaient été découvertes au XIXème siècle (le "genre" d'une variété par Riemann, les nombres de Betti, etc.). Mais la publication en 1895 de l'Analysis situs scellera le destin de la topologie moderne : Poincaré y expose en effet l'idée géniale d'associer aux variétés des invariants qui ne sont plus des nombres, mais des structures algébriques complètes ! Augurées par Lagrange et Galois, définitivement installées au cœur de la géométrie par Klein dans son programme d'Erlangen, ces structures sont des « groupes ». L'Analysis situs et ses compléments marquent ainsi la naissance d'une théorie aussi puissante que féconde, désormais omniprésente dans la quasi-totalité des branches des mathématiques modernes : la topologie algébrique (et sous une forme plus élaborée, l'algèbre homologique).
Les découvertes de Poincaré s'articulent autour de deux grandes idées : d'une part, il est possible d'associer à une variété ses « groupes d'homologiehomologie », d'où une nouvelle interprétation de la caractéristique d'Euler-Poincaré et des nombres de Betti (comme dimensions des groupes d'homologie) ; d'autre part, de nombreuses informations relativement à une variété peuvent être codées dans un objet appelé « groupe fondamental » (ou « groupe de Poincaré »). Les deux notions ne sont pas complètement étrangères puisque le premier groupe d'homologie se déduit aisément du groupe fondamental.5
Des élastiques au groupe fondamental
Après le papier et la colle, nous aurons maintenant besoin d'élastiques ! Plus exactement, l'objet mathématique qui nous intéresse porteporte le nom de « lacet » et, à quelques subtilités près, c'est simplement une courbe fermée dessinée sur une variété. Comme d'habitude en topologie, nous sommes libre de jouer à notre guise avec ces élastiques (sans toutefois les rompre) et lorsque l'on peut passer d'un lacet à l'autre par une déformation continue, on dit d'eux qu'ils sont « homotopes ». Sur le plan et la sphère, il n'est pas difficile de se convaincre que deux lacets sont toujours homotopes : nous verrons que cette propriété, baptisée « simple connexitéconnexité », joue un rôle essentiel dans la formulation de la conjectureconjecture de Poincaré.

Le plan est simplement connexe : deux lacets y sont toujours homotopes (ici une courbe fermée en « huit » et un cercle).
La sphère jouit également de cette propriété.
Crédits : S. Tummarello
La situation est cependant bien différente pour la plupart des autres variétés ! Par exemple, les lacets sur un cylindre se scindent en deux catégories : ceux qui sont enroulés autour du cylindre et les autres. Il est en effet impossible sur la figure ci-dessous de déformer continûment et en restant sur la surface du cylindre le lacet dessiné en vert pour obtenir celui en bleu . De même on peut identifier trois catégories de lacets pour le tore.

Sur le cylindre, les lacets tracés en vert et bleu ne sont pas homotopes.
Il en va de même pour ceux dessinés (en vert, bleu et rouge) sur le tore.
Crédits : S. Tummarello
L'objet du groupe fondamental6 est précisément de classer les lacets d'une variété selon qu'ils sont homotopes ou non (en incorporant au passage des informations supplémentaires - comme le "nombre d'enroulements"). La complexité d'une variété se reflète ainsi sur son groupe fondamental, et certaines opérations (comme les collages) se traduisent par des « calculs » sur les groupes fondamentaux. Cette passerellepasserelle a non seulement permis de profiter de la puissance de l'algèbre pour étudier des problèmes de nature topologique, mais au-delà d'unifier encore un peu plus cette vaste science que sont les mathématiques.
La conjecture de Poincaré
Une variété dont le groupe fondamental est le plus simple possible, tels le plan ou la sphère, est dite « simplement connexeconnexe ». À l'opposé, le tore, le cylindre, le ruban de Möbius et bien d'autres variétés ne sont pas simplement connexes. Parmi toutes les surfaces , la sphère occupe ainsi une position singulière, car c'est la seule à être à la fois sans bord, « compacte » (ce qui signifie grosso modo qu'elle est bornée dans l'espace, contrairement au plan) et simplement connexe.
Guidé par son intuition géniale, Poincaré a deviné que ces propriétés (absence de bord, compacité et simple connexité) caractérisaient non seulement la sphère usuelle mais aussi les sphères de dimension supérieure. Le cercle et la sphère ont en effet des grandes sœurs dans les espaces à quatre dimensions et plus. Mais sans détour, les équations s'avèrent bien plus parlantes que les figures pour décrire de tels objets : il suffit d'adapter l'équation de définition en y incorporant les coordonnées supplémentaires.

Les équations des sphères de dimension 3 et plus se calquent sur celles du cercle ou de la sphère usuelle.
Notons qu'une sphère à n dimensions baigne dans un espace à n+1 dimensions.
Crédits : S. Tummarello
La conjecture de Poincaré s'énonce finalement ainsi : toute variété compacte de dimension n=3 (ou plus), sans bord et simplement connexe, est homéomorphe à une sphère de dimension n. Au cours du XXème siècle, de nombreux travaux lui ont été consacré et dans les années 1961-62, la conjecture tombe pour toutes les dimensions supérieures ou égales à 5 (n=5 par Zeeman, n≥7 puis n≥5 par Smale, n=6 par Stallings). Vingt ans plus tard, le cas n=4 est démontré par Freedman (1982), si bien qu'il ne restait plus à traiter que le cas des variétés de dimension 3. Mais la difficulté monumentale de ce dernier volet lui valut de figurer parmi les sept « problèmes du millénaire » du Clay Mathematics Institute.
En 2002 et 2003, prolongeant les travaux de R. Hamilton (1982), Grigori Perelman publie sur InternetInternet trois articles où il réunit tous les ingrédients nécessaires pour démontrer complètement une prédiction due à W. Thurston à la fin des années 70 : la « conjecture de géométrisation ». Or celle-ci n'a pour conséquence pas moins que l'exactitude de la conjecture de Poincaré dans le cas n=3 ! Un siècle après le mathématicien français, Grigori Perelman a ainsi mis un point final à l'un des plus vieux problèmes de topologie.
1 Il y a débat quant à la paternité de la topologie, certains historienshistoriens l'attribuant à Leibniz, d'autres à Euler...
2 Un polyèdre est convexe si toutes ses diagonales sont contenues dans son intérieur.
3 H. Poincaré, Analyse de ses travaux scientifiques, Acta math., 38 (1921), p. 101.
4 Autrefois la topologie était appelée Analysis Situs, ou encore Geometria Situs.
5 En termes savants, les experts savent que le premier groupe d'homologie est l'abélianisé du groupe fondamental, i.e. le quotient du groupe fondamental par son commutateurcommutateur.
6 Les lecteurs initiés comprendront que "le" groupe fondamental ne concerne ici que les variétés connexes par arcs, pour lesquelles le "point-base" ne joue aucun rôle.