Avec la mécanique quantique, la relativité générale est l'un des monuments de la physique théorique du XXe siècle. Elle a été complétement formulée pendant le mois de novembre 1915 par Albert Einstein qui l'a découverte sur des bases presque purement conceptuelles et mathématiques. À l'occasion de son centenaire, puisque l'article final exposant cette théorie date du 25 novembre, nous vous proposons de (re)découvrir des articles et des dossiers que Futura-Sciences a consacrés à la théorie de la relativité et à ses implications en astrophysique et cosmologie.
au sommaire
Tout au long du mois de novembre 1915, et selon ses propres mots, Albert EinsteinEinstein a vécu la période la plus énervante et la plus éprouvante de toute sa vie, mais aussi la plus riche en résultats. Talonné par le mathématicienmathématicien David HilbertDavid Hilbert, Albert Einstein est lancé dans un sprint final qui va déboucher sur quatre articles présentés lors de la séance hebdomadaire de l'Académie de Sciences de Berlin. Leur contenu sera finalement rassemblé dans un article de synthèse publié en mars 1916. De quoi s'agissait-il ?
Rien de moins que des principes fondamentaux de sa théorie relativiste de la gravitation ainsi que du célèbre système d'équations reliant la courbure et la dynamique de la géométrie de l'espace-temps aux distributions d'impulsions et d'énergie qu'il contient. Le mois de novembre 1915 est par conséquent considéré comme le mois de naissance de la théorie de la relativité générale d'Einstein. Le centenaire de cette théorie a donc été fêté lors de nombreux colloques internationaux et le sera encore tout au long de cette année qui est aussi l'année internationale de sciences de la lumièrelumière.
Un extrait du nouveau film de l'Institut Henri Poincaré : Einstein et la Relativité Générale : une histoire singulière. Réalisation : Quentin Lazzarotto, co-auteurs : Jean-Philippe Uzan & Jean Eisenstaedt, Production : Look at sciences / RMC Découverte © Institut Henri Poincaré
Futura-Sciences célèbre aussi cet anniversaire qui a permis à l'humanité de pénétrer dans le monde de l'espace-temps, plat lors de la découverte de la théorie de la relativité restreinterelativité restreinte en 1905, puis courbe. Il faudra des dizaines d'années et le travail conjoint des physiciensphysiciens théoriciens et des mathématiciens pour explorer le contenu des équations de la théorie d'Einstein. Ce ne sera finalement qu'à partir des années 1960 que l'on commencera vraiment à pouvoir confronter ce contenu à des expériences et des observations. Aujourd'hui étoile à neutronsétoile à neutrons, trous noirstrous noirs, cosmologiecosmologie relativiste et ondes gravitationnellesondes gravitationnelles sont souvent sur le devant de la scène et Futura-Sciences a consacré de nombreux dossiers et articles à ces questions fascinantes. Nous vous proposons d'en (re)découvrir quelques-uns à l'occasion du centenaire de la relativité générale.
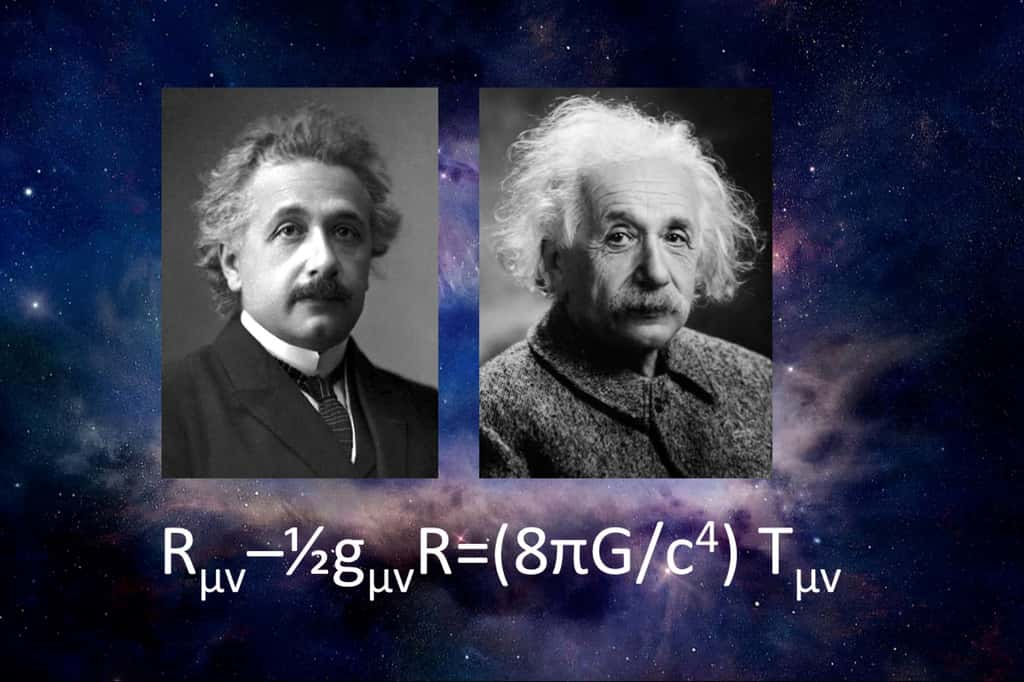
L'espace-temps et sa géométrie
La théorie de la relativité restreinte d'Einstein prend profondément racine dans la théorie électromagnétique de la lumière. Comme l'a expliqué Einstein dans une série de quatre conférences qu'il a données en 1921 à l'université de Princeton, les ondes lumineuses fournissent naturellement des moyens précis d'effectuer des mesures de longueurs, de duréesdurées et donc de vitessesvitesses. Ceci explique pourquoi elles ont été le révélateur expérimental - par exemple avec l'expérience de Michelson et Morley - aussi bien que théorique de l'existence d'une vitesse finie pour tous les phénomènes dans l'universunivers ainsi que de l'étonnante plasticitéplasticité du temps qui conduit à la frappante dilatationdilatation des durées. La fameuse formule de l'équivalence entre la massemasse et l'énergie est bien sûr une autre conséquence de cette vitesse limite et de l'exigence de l'invariance des lois de la nature pour des observateurs en mouvementsmouvements à vitesses constantes les uns par rapport aux autres.
Un documentaire en deux parties pour entrer en douceur dans le monde de l'espace-temps d'Einstein avec la dilatation des durées et la contraction des longueurs. © Jean-Pierre Luminet, YouTube
L'existence d'une vitesse limite indépassable, égale à celle de la lumière dans le vide, imposée à tous les objets (électrons ou photonsphotons par exemple) dans toutes les directions et à tous les observateurs en mouvement, a fait l'objet de nombreux tests de plus en plus précis depuis sa découverte par Einstein et il en est de même pour la dilatation des durées.
Un court moment, des faisceaux de neutrinosneutrinos transluminiques ont semblé contredire ce postulatpostulat de la théorie de la relativité restreinte mais l'explication résidait dans une erreur de l'expérience réalisée avec le détecteur Opera. Cependant, derrière le fameux paradoxe EPR mettant en jeu l'intrication quantiqueintrication quantique, se cache peut-être la propagation d'un signal allant beaucoup plus vite que la lumière.
Parce que l'espace-temps est courbé par la matière et l'énergie, il est à l'origine de la force de gravitation qui dévie les trajectoires des corps célestes et des rayons lumineux. La théorie des trous noirs repose grandement sur les modifications du comportement d'un réseau de rayons lumineux impliqués par les équations de la relativité générale. Il existe aussi des mirages gravitationnels (visibles à 20:00 sur cette vidéo) générés par la courbure de l'espace-temps, comme l'explique cette seconde partie du documentaire. On y parle des ondes gravitationnelles et de l'aspect d'un disque d'accrétion entourant un trou noir (23:00). © Jean-Pierre Luminet, Youtube
Déjà dans son article de 1905, Einstein avait fait remarquer que sa théorie reposait sur l'existence d'un groupe de transformations reliant les coordonnées d'espace et de temps des événements d'une façon nouvelle. Pour des mathématiciens comme Felix Klein et surtout Hermann Minkowski, l'existence de ce groupe impliquait celle d'une nouvelle géométrie, celle de l'espace-temps, dans laquelle des analogues des rotations dans l'espace mélangeaient les axes d'espace et de temps.
Pour ces mathématiciens du début du XXe siècle, la géométrie était aussi une affaire d'algèbre, plus précisément une question de théorie des invariants. Il s'agit d'une puissante théorie permettant de trouver tous les théorèmesthéorèmes de géométrie associés à des ensembles d'équations polynomiales décrivant des assemblages de courbes et de surfaces dans des espaces à N dimensions (voir à ce sujet les excellentes introductions à ces théories données par Klein et Dudley Ernest Littlewood qui permettent de bien comprendre les conférences d'Einstein à Princeton).
Cette géométrie algébrique, jointe au calcul infinitésimal, avait permis en particulier à Tullio Levi-Civita de développer la théorie générale des espaces courbes esquissée par Bernhard RiemannBernhard Riemann au XIXe siècle dans le cadre de ce que l'on appelait alors le calcul différentiel absolu.
Einstein n'était pas très à l'aise ni très intéressé initialement par cette approche de sa théorie de la relativité restreinte. Elle allait pourtant se révéler capitale pour la suite de ses recherches qui visaient à généraliser sa théorie pour qu'elle soit valable quel que soit le mouvement des observateurs et surtout pour qu'elle s'applique à la gravitation. Comme le rappelait Henri Poincaré dans le texte d'une conférence donnée à Lille en 1909, Laplace avait montré que la théorie de la gravitation de NewtonNewton impliquait que cette force universelle devait se propager au moins 10 millions de fois plus vite que la lumière. Il y avait donc un conflit avec un des postulats fondamentaux de la théorie de la relativité restreinte. Pour surmonter la contradiction, Einstein a finalement dû apprendre et comprendre les mathématiques du calcul tensoriel contenu dans la théorie des invariantsinvariants et du calcul différentiel absolu.
En effet, la théorie des invariants montre que les théorèmes de géométrie sont reliés à des quantités qui ne dépendent pas des systèmes de coordonnées utilisés et à des équations qui gardent une certaine forme sous l'action d'un groupe de transformations géométriques, des covariants et des contravariants selon le langage des mathématiciens. Si l'on postule que les lois de la nature sont les mêmes pour tous les observateurs quels que soient leur état de mouvement et les systèmes de coordonnées, on est naturellement conduit à chercher des équations qui sont des invariants et covariants de la géométrie de l'espace-temps. Le calcul différentiel absolu, qui fonctionne quelle que soit la géométrie et à N dimensions permet alors de trouver automatiquement ces lois.
Il faudra plusieurs années à Einstein, de 1907 à 1915, et au prix d'un travail herculéen en compagnie de son ami le mathématicien Marcel Grossmann, pour atteindre ce but.
Le lecteur l'aura compris, tant du point de vue conceptuel que mathématique, la théorie de la relativité, qu'elle soit restreinte ou générale, est un vaste sujet et c'est pourquoi Futura-Sciences a consacré deux dossiers aux fondements conceptuels des ces deux théories, à leur histoire et à leur développement depuis les travaux fondateurs d'Einstein :
Trous noirs et étoiles à neutrons, les astres relativistes

Dès sa naissance, la théorie de la relativité générale d'Einstein permettait de comprendre une anomalieanomalie du mouvement de la planète MercureMercure et elle prédisait aussi des déviations des rayons lumineux et un décalage spectral vers le rouge inédits. Il fallait tester ces prédictions qui différaient de celles de la théorie de Newton. Ce fut fait en mai 1919 par Sir Arthur Eddington et la célèbre Royal Astronomical Society qui organisèrent deux expéditions pour observer et mesurer le phénomène de déviation des rayons lumineux à l'occasion d'une éclipse totaleéclipse totale de SoleilSoleil qui pouvait être observée à Sobral, au Brésil, ainsi que sur l'île de Principe, dans le golfe de Guinée, au large de l'Afrique
Les étoiles de l'amas des HyadesHyades, bien visibles lors de l'éclipse, se révélèrent effectivement à des positions différentes sur la sphère céleste, déplacées de leurs positions habituelles par environ 1,75 seconde d'arcseconde d'arc, en bon accord avec les prédictions de la théorie de la gravitation d'Einstein mais pas du tout avec celle de la théorie de Newton.
Ce fut la panique chez bon nombre de physiciens de l'époque lorsqu'ils réalisèrent qu'ils devaient désormais étudier le calcul tensoriel et ses équations bardées d'indices, sans significations intuitives immédiates. Certains ne purent jamais s'habituer à la théorie d'Einstein et, malgré d'autres confirmations, ne crurent jamais en sa véracité.
Le grand astrophysicienastrophysicien indien Chandrasekhar a raconté à ce sujet une anecdote devenue célèbre. Peu de temps après les observations de Principe et Sobral, lorsque l'astrophysicien Edward Milne avait lancé à son collègue : « Eddington, vous devez être l'un des trois hommes au monde qui comprenne vraiment la théorie de la relativité générale d'Einstein », le silence de ce dernier le surprit. Il ajouta : « Ne soyez pas modeste, Eddington ». Sortant de son mutisme, ce dernier répliqua alors : « Au contraire, je cherche qui peut bien être ce troisième homme ! ».
Il y a certainement beaucoup d'exagération dans cette déclaration. Moins de deux mois après sa découverte des équations de la relativité générale, Einstein fit connaître le résultat auquel était parvenu en pleine guerre sur le front russe son collègue Karl Schwarzschild. Il ne s'agissait rien de moins que de la première solution exacte de ces équations aptes à décrire des étoiles et, nous le savons maintenant, des trous noirs. Il n'y a pas de doute non plus qu'en 1919 le mathématicien Hermann WeylHermann Weyl et le physicien Erwin SchrödingerErwin Schrödinger, pour ne citer qu'eux, comprenaient aussi très bien le travail d'Einstein.
De 1917 à 1918, celui-ci accomplit de nouveaux bonds de géant en fondant la cosmologie relativiste et la théorie des ondes gravitationnelles. Au cours des années 1930, il posa aussi les bases de la théorie des trous de ver et du phénomène de lentille gravitationnellelentille gravitationnelle. Aujourd'hui, comme le montre les liens ci-dessous, la recherche sur la physiquephysique des trous noirs et des étoiles relativistes est très active.
Le Big Bang et la cosmologie relativiste

Il en est de même de nos jours avec le modèle standard de la cosmologiemodèle standard de la cosmologie relativiste qui sert de base à la théorie du Big BangBig Bang. Il repose solidement sur la théorie de la nucléosynthèsenucléosynthèse primordiale et les mesures concernant le rayonnement fossilerayonnement fossile. Cela n'empêche pas les cosmologistes de tenter de dépasser ce modèle grâce à la théorie de l'inflation, laquelle conduit même à spéculer sur l'existence d'un multivers et d'un avant Big Bang. Futura-Sciences a consacré plusieurs articles et dossiers à ces questions.
Plusieurs articles historiques concernant les trous de ver, les trous noirs, la cosmologie et les tests de la relativité générale sont disponibles en téléchargement sur une page de l'American Physical Society à l'occasion du centenaire de la découverte de la relativité générale.