La géométrie non euclidienne

Quand on s'aperçut que la Terre n'était pas plate mais sphérique, de nombreux « faits » de la géométrie euclidienne qui semblaient évidents devinrent problématiques et ouvrirent la voie aux géométries non euclidiennes.

Chou romanesco Brassica oleracea var. botrytis. © Coyau CC BY-SA 3.0

La géométrie projective (géométrie non euclidienne) a introduit en peinture, les points à l'infini permettant ainsi de dessiner des tableaux avec une vue perspective exacte. © Domaine public

Ainsi, sur une sphère, les bateaux pouvaient voyager en ligne droite entre trois changements de direction (de 90°) et revenir à leur point de départpoint de départ. À mesure que les méthodes de calcul s'amélioraient, les géomètresgéomètres s'aperçurent que la somme des angles du triangle parcouru par le bateau était supérieure à 180°. Cette observation ouvrit la possibilité de nouvelles géométries, les géométries non euclidiennes.

La géométrie non euclidienne, la symétrie et la projection

Les symétries de la géométrie non euclidienne spécifient aussi ce qui reste invariant lors des opérations mathématiques. La géométrie projective s'intéresse à ce qui reste invariant quand des objets géométriques sont représentés dans un autre contexte ; par exemple, quand un objet à trois dimensions est projeté sur un plan à deux dimensions, est quand des figures tracées sur une sphère sont projetées sur un plan.

Comme le comprirent les artistes de la Renaissance italienne, dans la géométrie projective les parallèles se coupent ! La topologie traite de symétries encore plus étonnantes. Souvent désignée comme la géométrie du caoutchouc, la topologie étudie comment peuvent être transformés des objets quand on considère qu'ils sont faits de caoutchouc mou et flexible.

Imaginez, par exemple, un anneau vide comme une chambre à air. Cet objet peut, en théorie, être étiré et déformé pour se transformer en une tasse avec anseanse. Mais on ne peut pas, sans le déchirer et le recoller, transformer cet anneau en une sphère creuse ! En topologie, une chambre à air et une tasse à café sont symétriques, pas une sphère et une tasse !

La symétrie d'échelle

La symétrie d'échelle (ou symétrie de grandeur) est la pierre angulaire de la géométrie euclidienne : si les triangles et les cercles ne conservaient pas leurs propriétés quand ils sont dilatés ou contractés, l'essentiel de la géométrie euclidienne disparaîtrait. Dans le monde réel toutefois, cette symétrie d'échelle est absente. Par exemple, les fourmisfourmis et des araignéesaraignées géantes, comme on en voit parfois dans les films de science-fiction, ne survivraient pas car le rapport entre leurs volumes et leurs surfaces imposerait qu'elles aient des poumonspoumons énormes. La conception d'une patte d'éléphant est plus qu'un agrandissement d'une patte de souris.

La géométrie fractale

L'absence dans le monde réel des idéalisations de la géométrie euclidienne a amené le développement de la géométrie fractale. Cette géométrie englobe les phénomènes qui ont une sorte d'invariance d'échelle. Les fractales sont des objets mathématiques dont la caractéristique principale est d'être « autosimilaire », dans le sens où elles ont la même apparence quel que soit l'agrandissement. Cette symétrie d'échelle est différente de la symétrie euclidienne car, en géométrie euclidienne, l'agrandissement d'une partie du triangle ne ressemble pas au triangle tout entier.

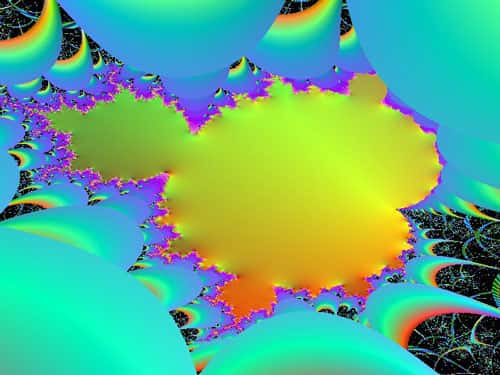
Ensemble de Mandelbrot, représentant le plus connu des fractales. © avi kedmi  Domaine public

L'ensemble de Mandelbrot est le plus célèbre des fractales. Les fractales sont communes dans la nature. Ainsi les côtes de la lande bretonne ont à peu près la même forme qu'elles soient vues d'un avion ou, en détail, du rivage. Les arbresarbres, les fougèresfougères et les choux ont des propriétés autosimilaires.

Le mathématicienmathématicien Kepler affirmait que la géométrie avait deux joyaux : le théorème de Pythagorethéorème de Pythagore et le nombre d'ornombre d'or. Nous examinerons ces beautés dans les chapitres suivants, mais depuis l'époque de Kepler de nouvelles géométries, incluant la topologie et les fractales, ont révélé d'autres pierres précieusespierres précieuses que nous allons partager.